How many dimensions are required to find an adversarial example?

Past work exploring adversarial vulnerability have focused on situations where an adversary can perturb all dimensions of model input. On the other hand, a range of recent works consider the case where either (i) an adversary can perturb a limited number of input parameters or (ii) a subset of modalities in a multimodal problem. In both of these cases, adversarial examples are effectively constrained to a subspace $V$ in the ambient input space $\mathcal{X}$. Motivated by this, in this work we investigate how adversarial vulnerability depends on $\dim(V)$. In particular, we show that the adversarial success of standard PGD attacks with $\ell^p$ norm constraints behaves like a monotonically increasing function of $\epsilon (\frac{\dim(V)}{\dim \mathcal{X}})^{\frac{1}{q}}$ where $\epsilon$ is the perturbation budget and $\frac{1}{p} + \frac{1}{q} =1$, provided $p > 1$ (the case $p=1$ presents additional subtleties which we analyze in some detail). This functional form can be easily derived from a simple toy linear model, and as such our results land further credence to arguments that adversarial examples are endemic to locally linear models on high dimensional spaces.

Convolutional networks inherit frequency sensitivity from image statistics

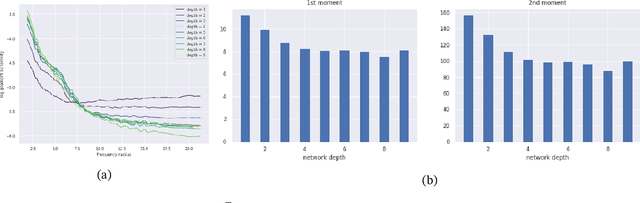
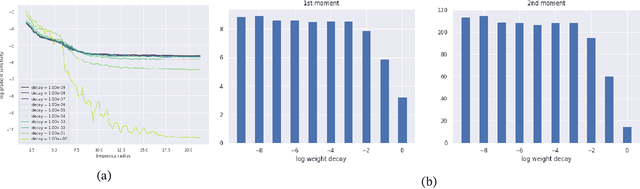
It is widely acknowledged that trained convolutional neural networks (CNNs) have different levels of sensitivity to signals of different frequency. In particular, a number of empirical studies have documented CNNs sensitivity to low-frequency signals. In this work we show with theory and experiments that this observed sensitivity is a consequence of the frequency distribution of natural images, which is known to have most of its power concentrated in low-to-mid frequencies. Our theoretical analysis relies on representations of the layers of a CNN in frequency space, an idea that has previously been used to accelerate computations and study implicit bias of network training algorithms, but to the best of our knowledge has not been applied in the domain of model robustness.