Haldane Bundles: A Dataset for Learning to Predict the Chern Number of Line Bundles on the Torus

Characteristic classes, which are abstract topological invariants associated with vector bundles, have become an important notion in modern physics with surprising real-world consequences. As a representative example, the incredible properties of topological insulators, which are insulators in their bulk but conductors on their surface, can be completely characterized by a specific characteristic class associated with their electronic band structure, the first Chern class. Given their importance to next generation computing and the computational challenge of calculating them using first-principles approaches, there is a need to develop machine learning approaches to predict the characteristic classes associated with a material system. To aid in this program we introduce the {\emph{Haldane bundle dataset}}, which consists of synthetically generated complex line bundles on the $2$-torus. We envision this dataset, which is not as challenging as noisy and sparsely measured real-world datasets but (as we show) still difficult for off-the-shelf architectures, to be a testing ground for architectures that incorporate the rich topological and geometric priors underlying characteristic classes.

ColMix -- A Simple Data Augmentation Framework to Improve Object Detector Performance and Robustness in Aerial Images

In the last decade, Convolutional Neural Network (CNN) and transformer based object detectors have achieved high performance on a large variety of datasets. Though the majority of detection literature has developed this capability on datasets such as MS COCO, these detectors have still proven effective for remote sensing applications. Challenges in this particular domain, such as small numbers of annotated objects and low object density, hinder overall performance. In this work, we present a novel augmentation method, called collage pasting, for increasing the object density without a need for segmentation masks, thereby improving the detector performance. We demonstrate that collage pasting improves precision and recall beyond related methods, such as mosaic augmentation, and enables greater control of object density. However, we find that collage pasting is vulnerable to certain out-of-distribution shifts, such as image corruptions. To address this, we introduce two simple approaches for combining collage pasting with PixMix augmentation method, and refer to our combined techniques as ColMix. Through extensive experiments, we show that employing ColMix results in detectors with superior performance on aerial imagery datasets and robust to various corruptions.

Neural frames: A Tool for Studying the Tangent Bundles Underlying Image Datasets and How Deep Learning Models Process Them

The assumption that many forms of high-dimensional data, such as images, actually live on low-dimensional manifolds, sometimes known as the manifold hypothesis, underlies much of our intuition for how and why deep learning works. Despite the central role that they play in our intuition, data manifolds are surprisingly hard to measure in the case of high-dimensional, sparsely sampled image datasets. This is particularly frustrating since the capability to measure data manifolds would provide a revealing window into the inner workings and dynamics of deep learning models. Motivated by this, we introduce neural frames, a novel and easy to use tool inspired by the notion of a frame from differential geometry. Neural frames can be used to explore the local neighborhoods of data manifolds as they pass through the hidden layers of neural networks even when one only has a single datapoint available. We present a mathematical framework for neural frames and explore some of their properties. We then use them to make a range of observations about how modern model architectures and training routines, such as heavy augmentation and adversarial training, affect the local behavior of a model.

In What Ways Are Deep Neural Networks Invariant and How Should We Measure This?

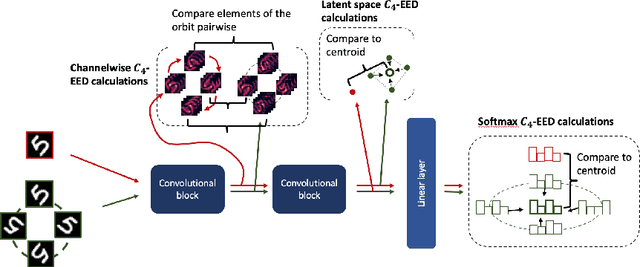
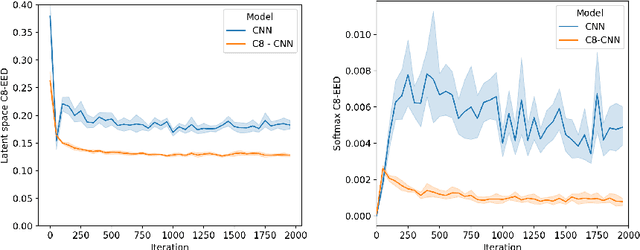
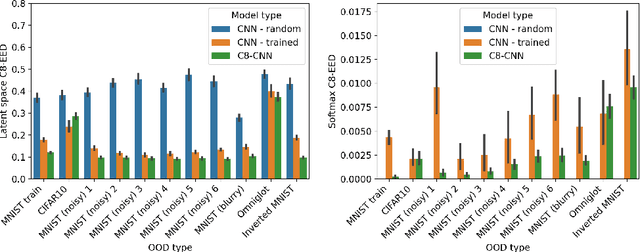
It is often said that a deep learning model is "invariant" to some specific type of transformation. However, what is meant by this statement strongly depends on the context in which it is made. In this paper we explore the nature of invariance and equivariance of deep learning models with the goal of better understanding the ways in which they actually capture these concepts on a formal level. We introduce a family of invariance and equivariance metrics that allows us to quantify these properties in a way that disentangles them from other metrics such as loss or accuracy. We use our metrics to better understand the two most popular methods used to build invariance into networks: data augmentation and equivariant layers. We draw a range of conclusions about invariance and equivariance in deep learning models, ranging from whether initializing a model with pretrained weights has an effect on a trained model's invariance, to the extent to which invariance learned via training can generalize to out-of-distribution data.

Convolutional networks inherit frequency sensitivity from image statistics

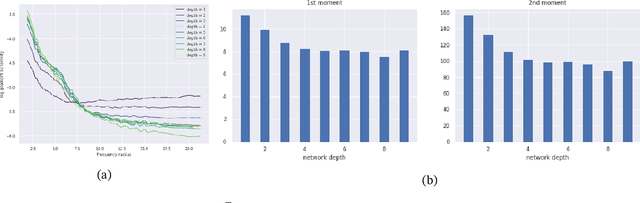
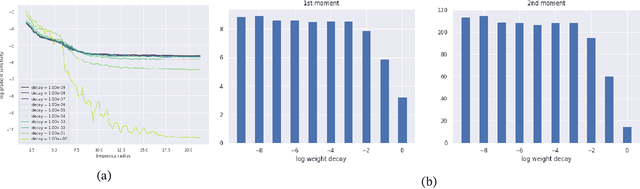
It is widely acknowledged that trained convolutional neural networks (CNNs) have different levels of sensitivity to signals of different frequency. In particular, a number of empirical studies have documented CNNs sensitivity to low-frequency signals. In this work we show with theory and experiments that this observed sensitivity is a consequence of the frequency distribution of natural images, which is known to have most of its power concentrated in low-to-mid frequencies. Our theoretical analysis relies on representations of the layers of a CNN in frequency space, an idea that has previously been used to accelerate computations and study implicit bias of network training algorithms, but to the best of our knowledge has not been applied in the domain of model robustness.