Graph Max Shift: A Hill-Climbing Method for Graph Clustering

We present a method for graph clustering that is analogous with gradient ascent methods previously proposed for clustering points in space. We show that, when applied to a random geometric graph with data iid from some density with Morse regularity, the method is asymptotically consistent. Here, consistency is understood with respect to a density-level clustering defined by the partition of the support of the density induced by the basins of attraction of the density modes.

An Axiomatic Definition of Hierarchical Clustering

In this paper, we take an axiomatic approach to defining a population hierarchical clustering for piecewise constant densities, and in a similar manner to Lebesgue integration, extend this definition to more general densities. When the density satisfies some mild conditions, e.g., when it has connected support, is continuous, and vanishes only at infinity, or when the connected components of the density satisfy these conditions, our axiomatic definition results in Hartigan's definition of cluster tree.

Haldane Bundles: A Dataset for Learning to Predict the Chern Number of Line Bundles on the Torus

Characteristic classes, which are abstract topological invariants associated with vector bundles, have become an important notion in modern physics with surprising real-world consequences. As a representative example, the incredible properties of topological insulators, which are insulators in their bulk but conductors on their surface, can be completely characterized by a specific characteristic class associated with their electronic band structure, the first Chern class. Given their importance to next generation computing and the computational challenge of calculating them using first-principles approaches, there is a need to develop machine learning approaches to predict the characteristic classes associated with a material system. To aid in this program we introduce the {\emph{Haldane bundle dataset}}, which consists of synthetically generated complex line bundles on the $2$-torus. We envision this dataset, which is not as challenging as noisy and sparsely measured real-world datasets but (as we show) still difficult for off-the-shelf architectures, to be a testing ground for architectures that incorporate the rich topological and geometric priors underlying characteristic classes.

Universal Fourier Attack for Time Series

A wide variety of adversarial attacks have been proposed and explored using image and audio data. These attacks are notoriously easy to generate digitally when the attacker can directly manipulate the input to a model, but are much more difficult to implement in the real-world. In this paper we present a universal, time invariant attack for general time series data such that the attack has a frequency spectrum primarily composed of the frequencies present in the original data. The universality of the attack makes it fast and easy to implement as no computation is required to add it to an input, while time invariance is useful for real-world deployment. Additionally, the frequency constraint ensures the attack can withstand filtering. We demonstrate the effectiveness of the attack in two different domains, speech recognition and unintended radiated emission, and show that the attack is robust against common transform-and-compare defense pipelines.

Deep Learning for Spectral Filling in Radio Frequency Applications

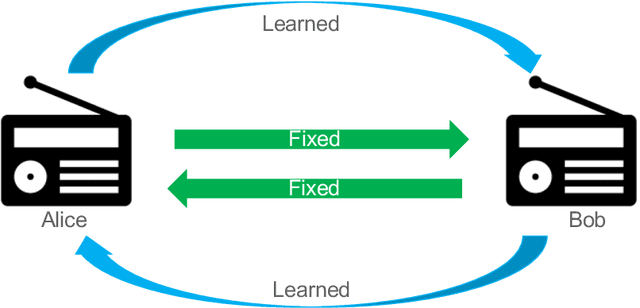
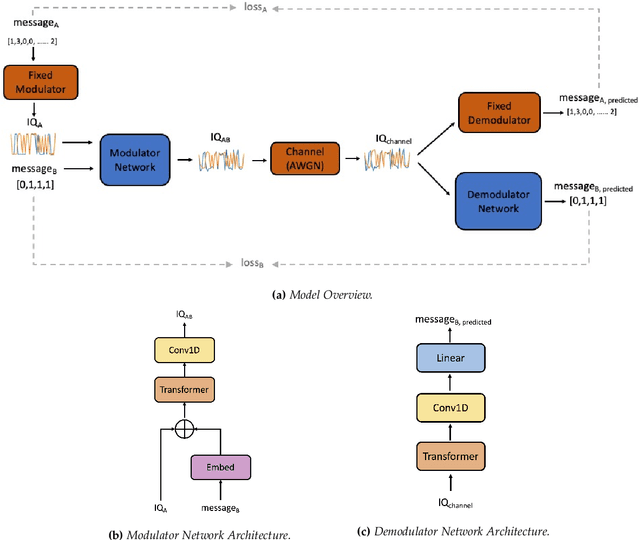
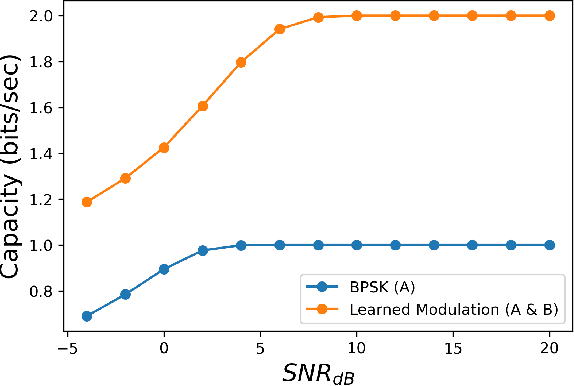
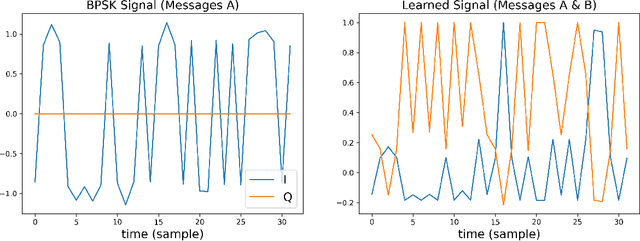
Due to the Internet of Things (IoT) proliferation, Radio Frequency (RF) channels are increasingly congested with new kinds of devices, which carry unique and diverse communication needs. This poses complex challenges in modern digital communications, and calls for the development of technological innovations that (i) optimize capacity (bitrate) in limited bandwidth environments, (ii) integrate cooperatively with already-deployed RF protocols, and (iii) are adaptive to the ever-changing demands in modern digital communications. In this paper we present methods for applying deep neural networks for spectral filling. Given an RF channel transmitting digital messages with a pre-established modulation scheme, we automatically learn novel modulation schemes for sending extra information, in the form of additional messages, "around" the fixed-modulation signals (i.e., without interfering with them). In so doing, we effectively increase channel capacity without increasing bandwidth. We further demonstrate the ability to generate signals that closely resemble the original modulations, such that the presence of extra messages is undetectable to third-party listeners. We present three computational experiments demonstrating the efficacy of our methods, and conclude by discussing the implications of our results for modern RF applications.

Fiber Bundle Morphisms as a Framework for Modeling Many-to-Many Maps

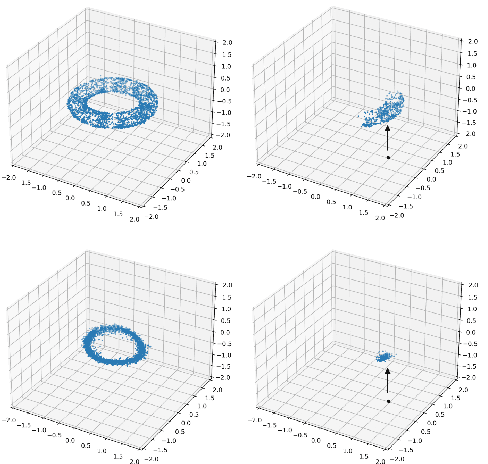
While it is not generally reflected in the `nice' datasets used for benchmarking machine learning algorithms, the real-world is full of processes that would be best described as many-to-many. That is, a single input can potentially yield many different outputs (whether due to noise, imperfect measurement, or intrinsic stochasticity in the process) and many different inputs can yield the same output (that is, the map is not injective). For example, imagine a sentiment analysis task where, due to linguistic ambiguity, a single statement can have a range of different sentiment interpretations while at the same time many distinct statements can represent the same sentiment. When modeling such a multivalued function $f: X \rightarrow Y$, it is frequently useful to be able to model the distribution on $f(x)$ for specific input $x$ as well as the distribution on fiber $f^{-1}(y)$ for specific output $y$. Such an analysis helps the user (i) better understand the variance intrinsic to the process they are studying and (ii) understand the range of specific input $x$ that can be used to achieve output $y$. Following existing work which used a fiber bundle framework to better model many-to-one processes, we describe how morphisms of fiber bundles provide a template for building models which naturally capture the structure of many-to-many processes.