Nico Courts
Fiber Bundle Morphisms as a Framework for Modeling Many-to-Many Maps
Mar 15, 2022


Abstract:While it is not generally reflected in the `nice' datasets used for benchmarking machine learning algorithms, the real-world is full of processes that would be best described as many-to-many. That is, a single input can potentially yield many different outputs (whether due to noise, imperfect measurement, or intrinsic stochasticity in the process) and many different inputs can yield the same output (that is, the map is not injective). For example, imagine a sentiment analysis task where, due to linguistic ambiguity, a single statement can have a range of different sentiment interpretations while at the same time many distinct statements can represent the same sentiment. When modeling such a multivalued function $f: X \rightarrow Y$, it is frequently useful to be able to model the distribution on $f(x)$ for specific input $x$ as well as the distribution on fiber $f^{-1}(y)$ for specific output $y$. Such an analysis helps the user (i) better understand the variance intrinsic to the process they are studying and (ii) understand the range of specific input $x$ that can be used to achieve output $y$. Following existing work which used a fiber bundle framework to better model many-to-one processes, we describe how morphisms of fiber bundles provide a template for building models which naturally capture the structure of many-to-many processes.
Bundle Networks: Fiber Bundles, Local Trivializations, and a Generative Approach to Exploring Many-to-one Maps
Oct 13, 2021



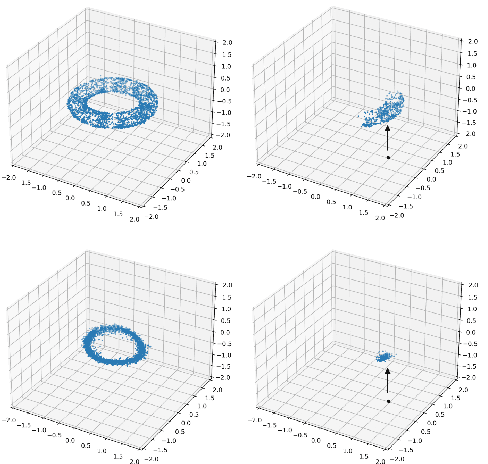
Abstract:Many-to-one maps are ubiquitous in machine learning, from the image recognition model that assigns a multitude of distinct images to the concept of "cat" to the time series forecasting model which assigns a range of distinct time-series to a single scalar regression value. While the primary use of such models is naturally to associate correct output to each input, in many problems it is also useful to be able to explore, understand, and sample from a model's fibers, which are the set of input values $x$ such that $f(x) = y$, for fixed $y$ in the output space. In this paper we show that popular generative architectures are ill-suited to such tasks. Motivated by this we introduce a novel generative architecture, a Bundle Network, based on the concept of a fiber bundle from (differential) topology. BundleNets exploit the idea of a local trivialization wherein a space can be locally decomposed into a product space that cleanly encodes the many-to-one nature of the map. By enforcing this decomposition in BundleNets and by utilizing state-of-the-art invertible components, investigating a network's fibers becomes natural.
One Representation to Rule Them All: Identifying Out-of-Support Examples in Few-shot Learning with Generic Representations
Jun 02, 2021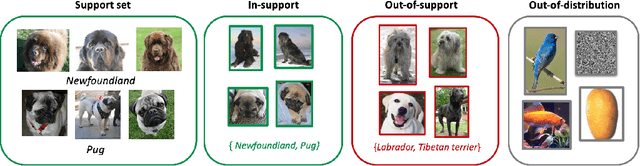
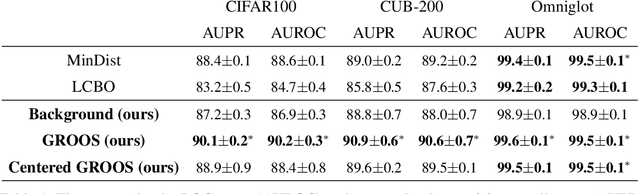
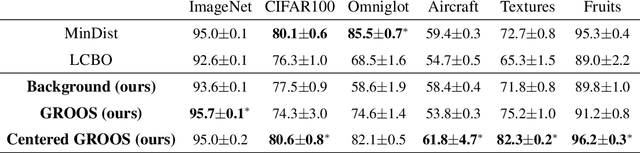
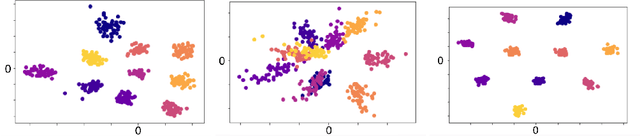
Abstract:The field of few-shot learning has made remarkable strides in developing powerful models that can operate in the small data regime. Nearly all of these methods assume every unlabeled instance encountered will belong to a handful of known classes for which one has examples. This can be problematic for real-world use cases where one routinely finds 'none-of-the-above' examples. In this paper we describe this challenge of identifying what we term 'out-of-support' (OOS) examples. We describe how this problem is subtly different from out-of-distribution detection and describe a new method of identifying OOS examples within the Prototypical Networks framework using a fixed point which we call the generic representation. We show that our method outperforms other existing approaches in the literature as well as other approaches that we propose in this paper. Finally, we investigate how the use of such a generic point affects the geometry of a model's feature space.
Fuzzy Simplicial Networks: A Topology-Inspired Model to Improve Task Generalization in Few-shot Learning
Sep 23, 2020


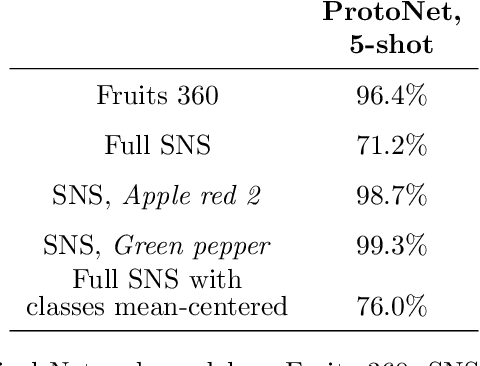
Abstract:Deep learning has shown great success in settings with massive amounts of data but has struggled when data is limited. Few-shot learning algorithms, which seek to address this limitation, are designed to generalize well to new tasks with limited data. Typically, models are evaluated on unseen classes and datasets that are defined by the same fundamental task as they are trained for (e.g. category membership). One can also ask how well a model can generalize to fundamentally different tasks within a fixed dataset (for example: moving from category membership to tasks that involve detecting object orientation or quantity). To formalize this kind of shift we define a notion of "independence of tasks" and identify three new sets of labels for established computer vision datasets that test a model's ability to generalize to tasks which draw on orthogonal attributes in the data. We use these datasets to investigate the failure modes of metric-based few-shot models. Based on our findings, we introduce a new few-shot model called Fuzzy Simplicial Networks (FSN) which leverages a construction from topology to more flexibly represent each class from limited data. In particular, FSN models can not only form multiple representations for a given class but can also begin to capture the low-dimensional structure which characterizes class manifolds in the encoded space of deep networks. We show that FSN outperforms state-of-the-art models on the challenging tasks we introduce in this paper while remaining competitive on standard few-shot benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge