Elliott Skomski
Adaptive Transfer Learning: a simple but effective transfer learning
Nov 22, 2021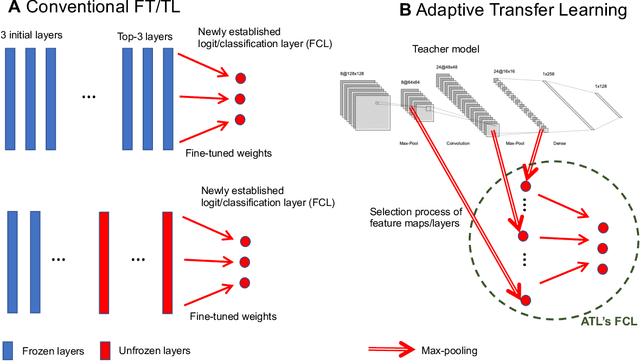
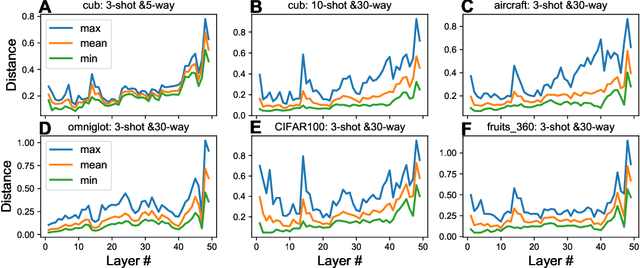
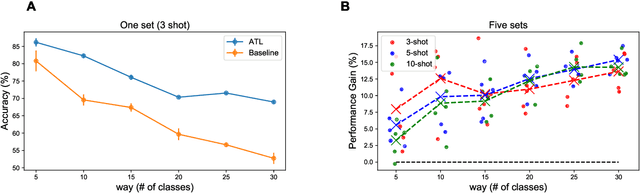
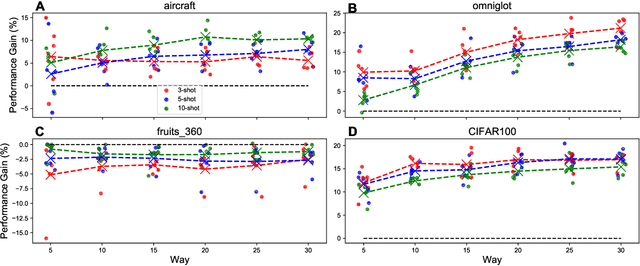
Abstract:Transfer learning (TL) leverages previously obtained knowledge to learn new tasks efficiently and has been used to train deep learning (DL) models with limited amount of data. When TL is applied to DL, pretrained (teacher) models are fine-tuned to build domain specific (student) models. This fine-tuning relies on the fact that DL model can be decomposed to classifiers and feature extractors, and a line of studies showed that the same feature extractors can be used to train classifiers on multiple tasks. Furthermore, recent studies proposed multiple algorithms that can fine-tune teacher models' feature extractors to train student models more efficiently. We note that regardless of the fine-tuning of feature extractors, the classifiers of student models are trained with final outputs of feature extractors (i.e., the outputs of penultimate layers). However, a recent study suggested that feature maps in ResNets across layers could be functionally equivalent, raising the possibility that feature maps inside the feature extractors can also be used to train student models' classifiers. Inspired by this study, we tested if feature maps in the hidden layers of the teacher models can be used to improve the student models' accuracy (i.e., TL's efficiency). Specifically, we developed 'adaptive transfer learning (ATL)', which can choose an optimal set of feature maps for TL, and tested it in the few-shot learning setting. Our empirical evaluations suggest that ATL can help DL models learn more efficiently, especially when available examples are limited.
Deep Learning Explicit Differentiable Predictive Control Laws for Buildings
Jul 25, 2021

Abstract:We present a differentiable predictive control (DPC) methodology for learning constrained control laws for unknown nonlinear systems. DPC poses an approximate solution to multiparametric programming problems emerging from explicit nonlinear model predictive control (MPC). Contrary to approximate MPC, DPC does not require supervision by an expert controller. Instead, a system dynamics model is learned from the observed system's dynamics, and the neural control law is optimized offline by leveraging the differentiable closed-loop system model. The combination of a differentiable closed-loop system and penalty methods for constraint handling of system outputs and inputs allows us to optimize the control law's parameters directly by backpropagating economic MPC loss through the learned system model. The control performance of the proposed DPC method is demonstrated in simulation using learned model of multi-zone building thermal dynamics.
One Representation to Rule Them All: Identifying Out-of-Support Examples in Few-shot Learning with Generic Representations
Jun 02, 2021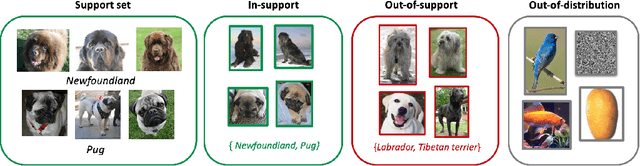
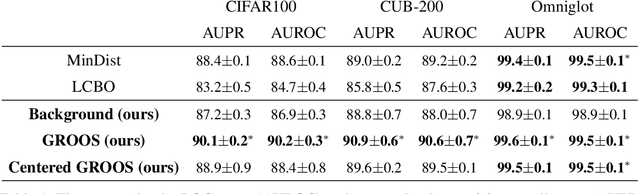
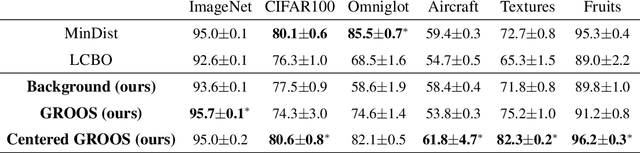
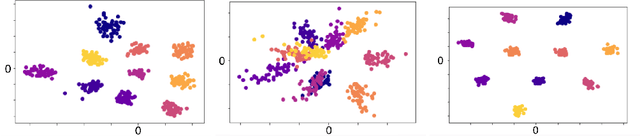
Abstract:The field of few-shot learning has made remarkable strides in developing powerful models that can operate in the small data regime. Nearly all of these methods assume every unlabeled instance encountered will belong to a handful of known classes for which one has examples. This can be problematic for real-world use cases where one routinely finds 'none-of-the-above' examples. In this paper we describe this challenge of identifying what we term 'out-of-support' (OOS) examples. We describe how this problem is subtly different from out-of-distribution detection and describe a new method of identifying OOS examples within the Prototypical Networks framework using a fixed point which we call the generic representation. We show that our method outperforms other existing approaches in the literature as well as other approaches that we propose in this paper. Finally, we investigate how the use of such a generic point affects the geometry of a model's feature space.
Prototypical Region Proposal Networks for Few-Shot Localization and Classification
Apr 08, 2021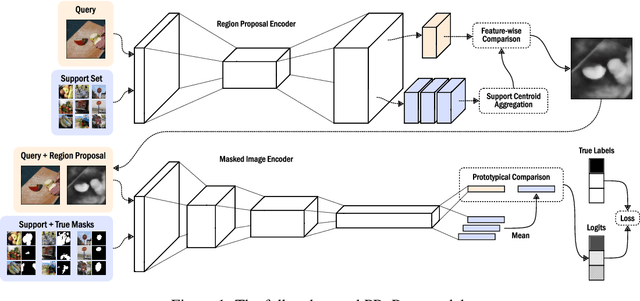
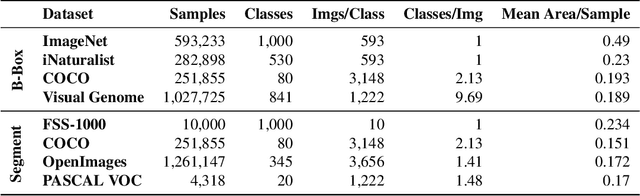
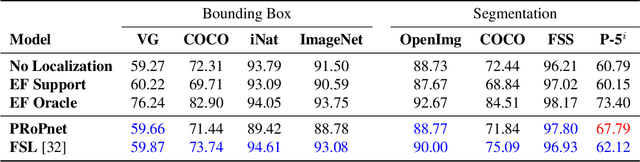
Abstract:Recently proposed few-shot image classification methods have generally focused on use cases where the objects to be classified are the central subject of images. Despite success on benchmark vision datasets aligned with this use case, these methods typically fail on use cases involving densely-annotated, busy images: images common in the wild where objects of relevance are not the central subject, instead appearing potentially occluded, small, or among other incidental objects belonging to other classes of potential interest. To localize relevant objects, we employ a prototype-based few-shot segmentation model which compares the encoded features of unlabeled query images with support class centroids to produce region proposals indicating the presence and location of support set classes in a query image. These region proposals are then used as additional conditioning input to few-shot image classifiers. We develop a framework to unify the two stages (segmentation and classification) into an end-to-end classification model -- PRoPnet -- and empirically demonstrate that our methods improve accuracy on image datasets with natural scenes containing multiple object classes.
Constrained Block Nonlinear Neural Dynamical Models
Jan 06, 2021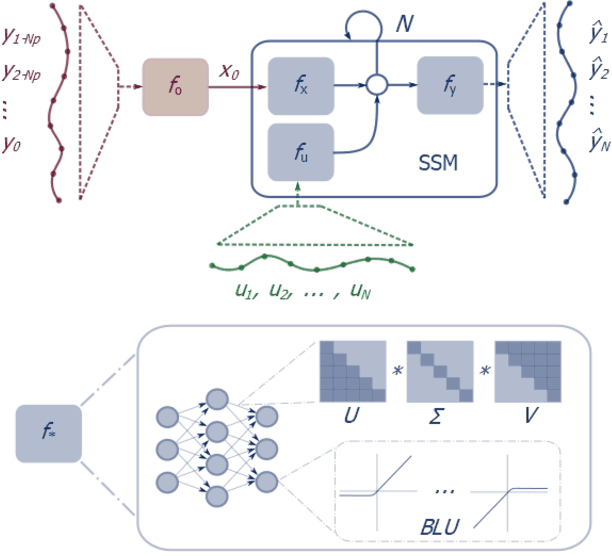


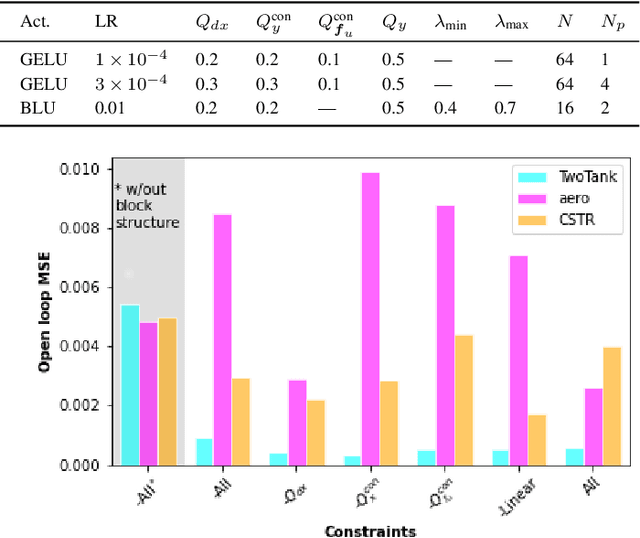
Abstract:Neural network modules conditioned by known priors can be effectively trained and combined to represent systems with nonlinear dynamics. This work explores a novel formulation for data-efficient learning of deep control-oriented nonlinear dynamical models by embedding local model structure and constraints. The proposed method consists of neural network blocks that represent input, state, and output dynamics with constraints placed on the network weights and system variables. For handling partially observable dynamical systems, we utilize a state observer neural network to estimate the states of the system's latent dynamics. We evaluate the performance of the proposed architecture and training methods on system identification tasks for three nonlinear systems: a continuous stirred tank reactor, a two tank interacting system, and an aerodynamics body. Models optimized with a few thousand system state observations accurately represent system dynamics in open loop simulation over thousands of time steps from a single set of initial conditions. Experimental results demonstrate an order of magnitude reduction in open-loop simulation mean squared error for our constrained, block-structured neural models when compared to traditional unstructured and unconstrained neural network models.
Physics-Informed Neural State Space Models via Learning and Evolution
Nov 26, 2020



Abstract:Recent works exploring deep learning application to dynamical systems modeling have demonstrated that embedding physical priors into neural networks can yield more effective, physically-realistic, and data-efficient models. However, in the absence of complete prior knowledge of a dynamical system's physical characteristics, determining the optimal structure and optimization strategy for these models can be difficult. In this work, we explore methods for discovering neural state space dynamics models for system identification. Starting with a design space of block-oriented state space models and structured linear maps with strong physical priors, we encode these components into a model genome alongside network structure, penalty constraints, and optimization hyperparameters. Demonstrating the overall utility of the design space, we employ an asynchronous genetic search algorithm that alternates between model selection and optimization and obtains accurate physically consistent models of three physical systems: an aerodynamics body, a continuous stirred tank reactor, and a two tank interacting system.
Spectral Analysis and Stability of Deep Neural Dynamics
Nov 26, 2020



Abstract:Our modern history of deep learning follows the arc of famous emergent disciplines in engineering (e.g. aero- and fluid dynamics) when theory lagged behind successful practical applications. Viewing neural networks from a dynamical systems perspective, in this work, we propose a novel characterization of deep neural networks as pointwise affine maps, making them accessible to a broader range of analysis methods to help close the gap between theory and practice. We begin by showing the equivalence of neural networks with parameter-varying affine maps parameterized by the state (feature) vector. As the paper's main results, we provide necessary and sufficient conditions for the global stability of generic deep feedforward neural networks. Further, we identify links between the spectral properties of layer-wise weight parametrizations, different activation functions, and their effect on the overall network's eigenvalue spectra. We analyze a range of neural networks with varying weight initializations, activation functions, bias terms, and depths. Our view of neural networks as affine parameter varying maps allows us to "crack open the black box" of global neural network dynamical behavior through visualization of stationary points, regions of attraction, state-space partitioning, eigenvalue spectra, and stability properties. Our analysis covers neural networks both as an end-to-end function and component-wise without simplifying assumptions or approximations. The methods we develop here provide tools to establish relationships between global neural dynamical properties and their constituent components which can aid in the principled design of neural networks for dynamics modeling and optimal control.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge