Domain-aware Control-oriented Neural Models for Autonomous Underwater Vehicles

Conventional physics-based modeling is a time-consuming bottleneck in control design for complex nonlinear systems like autonomous underwater vehicles (AUVs). In contrast, purely data-driven models, though convenient and quick to obtain, require a large number of observations and lack operational guarantees for safety-critical systems. Data-driven models leveraging available partially characterized dynamics have potential to provide reliable systems models in a typical data-limited scenario for high value complex systems, thereby avoiding months of expensive expert modeling time. In this work we explore this middle-ground between expert-modeled and pure data-driven modeling. We present control-oriented parametric models with varying levels of domain-awareness that exploit known system structure and prior physics knowledge to create constrained deep neural dynamical system models. We employ universal differential equations to construct data-driven blackbox and graybox representations of the AUV dynamics. In addition, we explore a hybrid formulation that explicitly models the residual error related to imperfect graybox models. We compare the prediction performance of the learned models for different distributions of initial conditions and control inputs to assess their accuracy, generalization, and suitability for control.

Deep Learning Explicit Differentiable Predictive Control Laws for Buildings

We present a differentiable predictive control (DPC) methodology for learning constrained control laws for unknown nonlinear systems. DPC poses an approximate solution to multiparametric programming problems emerging from explicit nonlinear model predictive control (MPC). Contrary to approximate MPC, DPC does not require supervision by an expert controller. Instead, a system dynamics model is learned from the observed system's dynamics, and the neural control law is optimized offline by leveraging the differentiable closed-loop system model. The combination of a differentiable closed-loop system and penalty methods for constraint handling of system outputs and inputs allows us to optimize the control law's parameters directly by backpropagating economic MPC loss through the learned system model. The control performance of the proposed DPC method is demonstrated in simulation using learned model of multi-zone building thermal dynamics.

Constrained Block Nonlinear Neural Dynamical Models

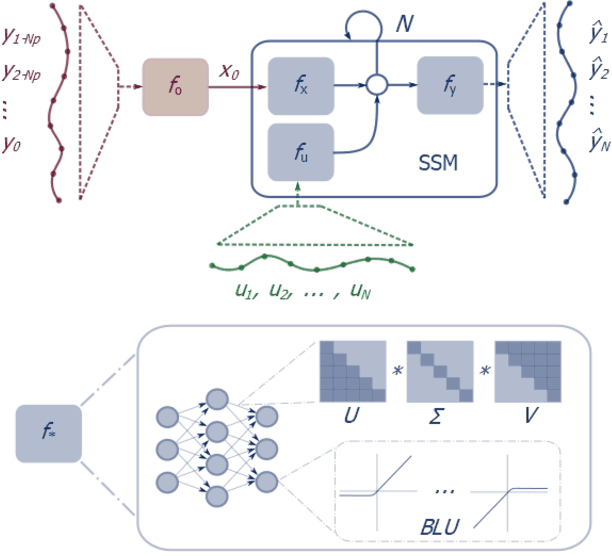
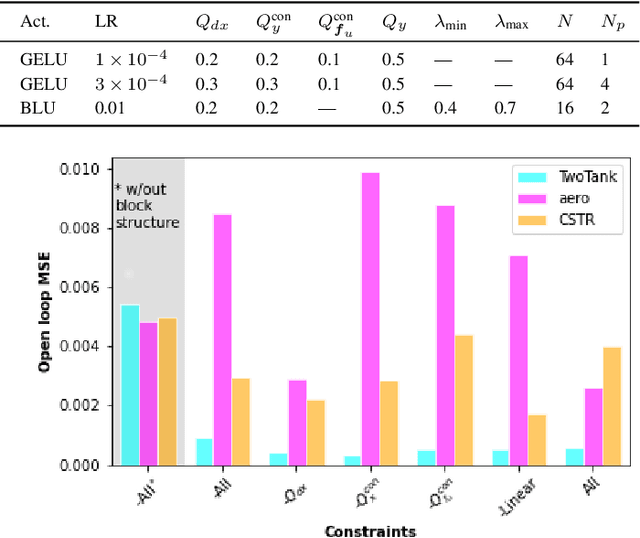
Neural network modules conditioned by known priors can be effectively trained and combined to represent systems with nonlinear dynamics. This work explores a novel formulation for data-efficient learning of deep control-oriented nonlinear dynamical models by embedding local model structure and constraints. The proposed method consists of neural network blocks that represent input, state, and output dynamics with constraints placed on the network weights and system variables. For handling partially observable dynamical systems, we utilize a state observer neural network to estimate the states of the system's latent dynamics. We evaluate the performance of the proposed architecture and training methods on system identification tasks for three nonlinear systems: a continuous stirred tank reactor, a two tank interacting system, and an aerodynamics body. Models optimized with a few thousand system state observations accurately represent system dynamics in open loop simulation over thousands of time steps from a single set of initial conditions. Experimental results demonstrate an order of magnitude reduction in open-loop simulation mean squared error for our constrained, block-structured neural models when compared to traditional unstructured and unconstrained neural network models.

Spectral Analysis and Stability of Deep Neural Dynamics

Our modern history of deep learning follows the arc of famous emergent disciplines in engineering (e.g. aero- and fluid dynamics) when theory lagged behind successful practical applications. Viewing neural networks from a dynamical systems perspective, in this work, we propose a novel characterization of deep neural networks as pointwise affine maps, making them accessible to a broader range of analysis methods to help close the gap between theory and practice. We begin by showing the equivalence of neural networks with parameter-varying affine maps parameterized by the state (feature) vector. As the paper's main results, we provide necessary and sufficient conditions for the global stability of generic deep feedforward neural networks. Further, we identify links between the spectral properties of layer-wise weight parametrizations, different activation functions, and their effect on the overall network's eigenvalue spectra. We analyze a range of neural networks with varying weight initializations, activation functions, bias terms, and depths. Our view of neural networks as affine parameter varying maps allows us to "crack open the black box" of global neural network dynamical behavior through visualization of stationary points, regions of attraction, state-space partitioning, eigenvalue spectra, and stability properties. Our analysis covers neural networks both as an end-to-end function and component-wise without simplifying assumptions or approximations. The methods we develop here provide tools to establish relationships between global neural dynamical properties and their constituent components which can aid in the principled design of neural networks for dynamics modeling and optimal control.