Learning to Optimize for Mixed-Integer Non-linear Programming

Mixed-integer non-linear programs (MINLPs) arise in various domains, such as energy systems and transportation, but are notoriously difficult to solve. Recent advances in machine learning have led to remarkable successes in optimization tasks, an area broadly known as learning to optimize. This approach includes using predictive models to generate solutions for optimization problems with continuous decision variables, thereby avoiding the need for computationally expensive optimization algorithms. However, applying learning to MINLPs remains challenging primarily due to the presence of integer decision variables, which complicate gradient-based learning. To address this limitation, we propose two differentiable correction layers that generate integer outputs while preserving gradient information. Combined with a soft penalty for constraint violation, our framework can tackle both the integrality and non-linear constraints in a MINLP. Experiments on three problem classes with convex/non-convex objective/constraints and integer/mixed-integer variables show that the proposed learning-based approach consistently produces high-quality solutions for parametric MINLPs extremely quickly. As problem size increases, traditional exact solvers and heuristic methods struggle to find feasible solutions, whereas our approach continues to deliver reliable results. Our work extends the scope of learning-to-optimize to MINLP, paving the way for integrating integer constraints into deep learning models. Our code is available at https://github.com/pnnl/L2O-pMINLP.

Differentiable Predictive Control for Large-Scale Urban Road Networks

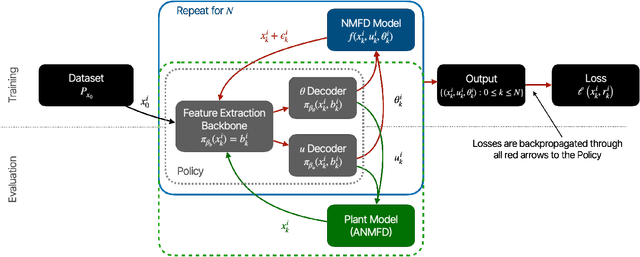
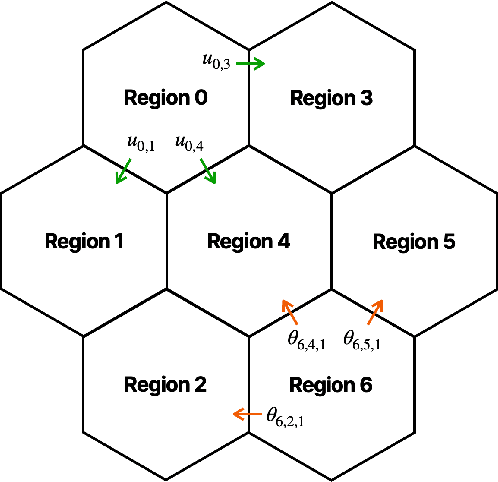
Transportation is a major contributor to CO2 emissions, making it essential to optimize traffic networks to reduce energy-related emissions. This paper presents a novel approach to traffic network control using Differentiable Predictive Control (DPC), a physics-informed machine learning methodology. We base our model on the Macroscopic Fundamental Diagram (MFD) and the Networked Macroscopic Fundamental Diagram (NMFD), offering a simplified representation of citywide traffic networks. Our approach ensures compliance with system constraints by construction. In empirical comparisons with existing state-of-the-art Model Predictive Control (MPC) methods, our approach demonstrates a 4 order of magnitude reduction in computation time and an up to 37% improvement in traffic performance. Furthermore, we assess the robustness of our controller to scenario shifts and find that it adapts well to changes in traffic patterns. This work proposes more efficient traffic control methods, particularly in large-scale urban networks, and aims to mitigate emissions and alleviate congestion in the future.

Physics-Informed Machine Learning for Modeling and Control of Dynamical Systems

Physics-informed machine learning (PIML) is a set of methods and tools that systematically integrate machine learning (ML) algorithms with physical constraints and abstract mathematical models developed in scientific and engineering domains. As opposed to purely data-driven methods, PIML models can be trained from additional information obtained by enforcing physical laws such as energy and mass conservation. More broadly, PIML models can include abstract properties and conditions such as stability, convexity, or invariance. The basic premise of PIML is that the integration of ML and physics can yield more effective, physically consistent, and data-efficient models. This paper aims to provide a tutorial-like overview of the recent advances in PIML for dynamical system modeling and control. Specifically, the paper covers an overview of the theory, fundamental concepts and methods, tools, and applications on topics of: 1) physics-informed learning for system identification; 2) physics-informed learning for control; 3) analysis and verification of PIML models; and 4) physics-informed digital twins. The paper is concluded with a perspective on open challenges and future research opportunities.

Proceedings of AAAI 2022 Fall Symposium: The Role of AI in Responding to Climate Challenges

Climate change is one of the most pressing challenges of our time, requiring rapid action across society. As artificial intelligence tools (AI) are rapidly deployed, it is therefore crucial to understand how they will impact climate action. On the one hand, AI can support applications in climate change mitigation (reducing or preventing greenhouse gas emissions), adaptation (preparing for the effects of a changing climate), and climate science. These applications have implications in areas ranging as widely as energy, agriculture, and finance. At the same time, AI is used in many ways that hinder climate action (e.g., by accelerating the use of greenhouse gas-emitting fossil fuels). In addition, AI technologies have a carbon and energy footprint themselves. This symposium brought together participants from across academia, industry, government, and civil society to explore these intersections of AI with climate change, as well as how each of these sectors can contribute to solutions.

Domain-aware Control-oriented Neural Models for Autonomous Underwater Vehicles

Conventional physics-based modeling is a time-consuming bottleneck in control design for complex nonlinear systems like autonomous underwater vehicles (AUVs). In contrast, purely data-driven models, though convenient and quick to obtain, require a large number of observations and lack operational guarantees for safety-critical systems. Data-driven models leveraging available partially characterized dynamics have potential to provide reliable systems models in a typical data-limited scenario for high value complex systems, thereby avoiding months of expensive expert modeling time. In this work we explore this middle-ground between expert-modeled and pure data-driven modeling. We present control-oriented parametric models with varying levels of domain-awareness that exploit known system structure and prior physics knowledge to create constrained deep neural dynamical system models. We employ universal differential equations to construct data-driven blackbox and graybox representations of the AUV dynamics. In addition, we explore a hybrid formulation that explicitly models the residual error related to imperfect graybox models. We compare the prediction performance of the learned models for different distributions of initial conditions and control inputs to assess their accuracy, generalization, and suitability for control.

Neural Lyapunov Differentiable Predictive Control

We present a learning-based predictive control methodology using the differentiable programming framework with probabilistic Lyapunov-based stability guarantees. The neural Lyapunov differentiable predictive control (NLDPC) learns the policy by constructing a computational graph encompassing the system dynamics, state and input constraints, and the necessary Lyapunov certification constraints, and thereafter using the automatic differentiation to update the neural policy parameters. In conjunction, our approach jointly learns a Lyapunov function that certifies the regions of state-space with stable dynamics. We also provide a sampling-based statistical guarantee for the training of NLDPC from the distribution of initial conditions. Our offline training approach provides a computationally efficient and scalable alternative to classical explicit model predictive control solutions. We substantiate the advantages of the proposed approach with simulations to stabilize the double integrator model and on an example of controlling an aircraft model.

Neural Ordinary Differential Equations for Nonlinear System Identification

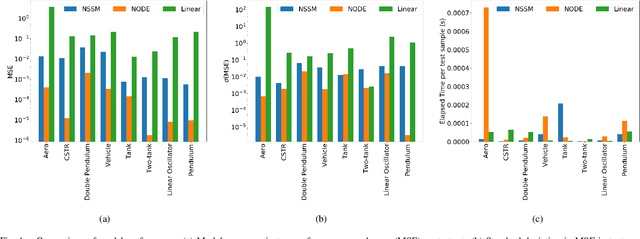
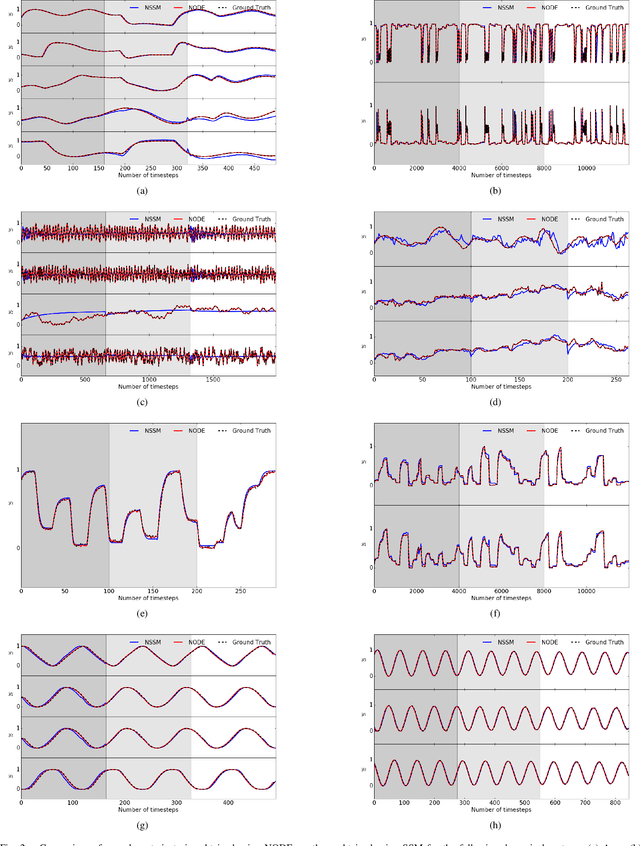
Neural ordinary differential equations (NODE) have been recently proposed as a promising approach for nonlinear system identification tasks. In this work, we systematically compare their predictive performance with current state-of-the-art nonlinear and classical linear methods. In particular, we present a quantitative study comparing NODE's performance against neural state-space models and classical linear system identification methods. We evaluate the inference speed and prediction performance of each method on open-loop errors across eight different dynamical systems. The experiments show that NODEs can consistently improve the prediction accuracy by an order of magnitude compared to benchmark methods. Besides improved accuracy, we also observed that NODEs are less sensitive to hyperparameters compared to neural state-space models. On the other hand, these performance gains come with a slight increase of computation at the inference time.

Learning Stochastic Parametric Differentiable Predictive Control Policies

The problem of synthesizing stochastic explicit model predictive control policies is known to be quickly intractable even for systems of modest complexity when using classical control-theoretic methods. To address this challenge, we present a scalable alternative called stochastic parametric differentiable predictive control (SP-DPC) for unsupervised learning of neural control policies governing stochastic linear systems subject to nonlinear chance constraints. SP-DPC is formulated as a deterministic approximation to the stochastic parametric constrained optimal control problem. This formulation allows us to directly compute the policy gradients via automatic differentiation of the problem's value function, evaluated over sampled parameters and uncertainties. In particular, the computed expectation of the SP-DPC problem's value function is backpropagated through the closed-loop system rollouts parametrized by a known nominal system dynamics model and neural control policy which allows for direct model-based policy optimization. We provide theoretical probabilistic guarantees for policies learned via the SP-DPC method on closed-loop stability and chance constraints satisfaction. Furthermore, we demonstrate the computational efficiency and scalability of the proposed policy optimization algorithm in three numerical examples, including systems with a large number of states or subject to nonlinear constraints.

On the Stochastic Stability of Deep Markov Models

Deep Markov models (DMM) are generative models that are scalable and expressive generalization of Markov models for representation, learning, and inference problems. However, the fundamental stochastic stability guarantees of such models have not been thoroughly investigated. In this paper, we provide sufficient conditions of DMM's stochastic stability as defined in the context of dynamical systems and propose a stability analysis method based on the contraction of probabilistic maps modeled by deep neural networks. We make connections between the spectral properties of neural network's weights and different types of used activation functions on the stability and overall dynamic behavior of DMMs with Gaussian distributions. Based on the theory, we propose a few practical methods for designing constrained DMMs with guaranteed stability. We empirically substantiate our theoretical results via intuitive numerical experiments using the proposed stability constraints.

Constructing Neural Network-Based Models for Simulating Dynamical Systems

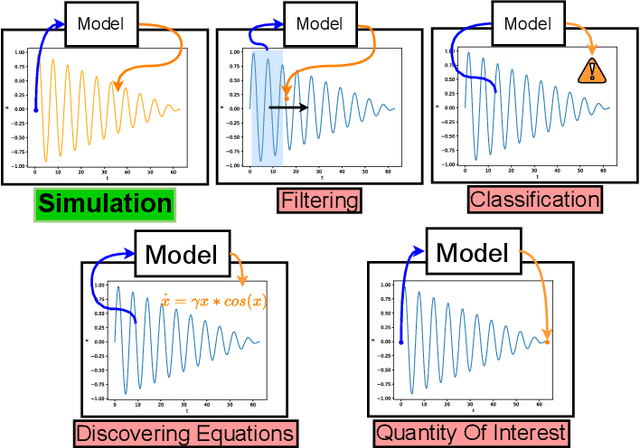
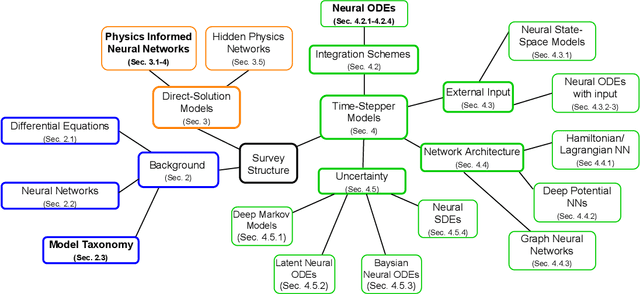
Dynamical systems see widespread use in natural sciences like physics, biology, chemistry, as well as engineering disciplines such as circuit analysis, computational fluid dynamics, and control. For simple systems, the differential equations governing the dynamics can be derived by applying fundamental physical laws. However, for more complex systems, this approach becomes exceedingly difficult. Data-driven modeling is an alternative paradigm that seeks to learn an approximation of the dynamics of a system using observations of the true system. In recent years, there has been an increased interest in data-driven modeling techniques, in particular neural networks have proven to provide an effective framework for solving a wide range of tasks. This paper provides a survey of the different ways to construct models of dynamical systems using neural networks. In addition to the basic overview, we review the related literature and outline the most significant challenges from numerical simulations that this modeling paradigm must overcome. Based on the reviewed literature and identified challenges, we provide a discussion on promising research areas.