Spatially temporally distributed informative path planning for multi-robot systems

This paper investigates the problem of informative path planning for a mobile robotic sensor network in spatially temporally distributed mapping. The robots are able to gather noisy measurements from an area of interest during their movements to build a Gaussian Process (GP) model of a spatio-temporal field. The model is then utilized to predict the spatio-temporal phenomenon at different points of interest. To spatially and temporally navigate the group of robots so that they can optimally acquire maximal information gains while their connectivity is preserved, we propose a novel multistep prediction informative path planning optimization strategy employing our newly defined local cost functions. By using the dual decomposition method, it is feasible and practical to effectively solve the optimization problem in a distributed manner. The proposed method was validated through synthetic experiments utilizing real-world data sets.

Physics-Informed Machine Learning for Modeling and Control of Dynamical Systems

Physics-informed machine learning (PIML) is a set of methods and tools that systematically integrate machine learning (ML) algorithms with physical constraints and abstract mathematical models developed in scientific and engineering domains. As opposed to purely data-driven methods, PIML models can be trained from additional information obtained by enforcing physical laws such as energy and mass conservation. More broadly, PIML models can include abstract properties and conditions such as stability, convexity, or invariance. The basic premise of PIML is that the integration of ML and physics can yield more effective, physically consistent, and data-efficient models. This paper aims to provide a tutorial-like overview of the recent advances in PIML for dynamical system modeling and control. Specifically, the paper covers an overview of the theory, fundamental concepts and methods, tools, and applications on topics of: 1) physics-informed learning for system identification; 2) physics-informed learning for control; 3) analysis and verification of PIML models; and 4) physics-informed digital twins. The paper is concluded with a perspective on open challenges and future research opportunities.

Ensemble Gaussian Processes for Adaptive Autonomous Driving on Multi-friction Surfaces

Driving under varying road conditions is challenging, especially for autonomous vehicles that must adapt in real-time to changes in the environment, e.g., rain, snow, etc. It is difficult to apply offline learning-based methods in these time-varying settings, as the controller should be trained on datasets representing all conditions it might encounter in the future. While online learning may adapt a model from real-time data, its convergence is often too slow for fast varying road conditions. We study this problem in autonomous racing, where driving at the limits of handling under varying road conditions is required for winning races. We propose a computationally-efficient approach that leverages an ensemble of Gaussian processes (GPs) to generalize and adapt pre-trained GPs to unseen conditions. Each GP is trained on driving data with a different road surface friction. A time-varying convex combination of these GPs is used within a model predictive control (MPC) framework, where the model weights are adapted online to the current road condition based on real-time data. The predictive variance of the ensemble Gaussian process (EGP) model allows the controller to account for prediction uncertainty and enables safe autonomous driving. Extensive simulations of a full scale autonomous car demonstrated the effectiveness of our proposed EGP-MPC method for providing good tracking performance in varying road conditions and the ability to generalize to unknown maps.

ADMM-based Adaptive Sampling Strategy for Nonholonomic Mobile Robotic Sensor Networks

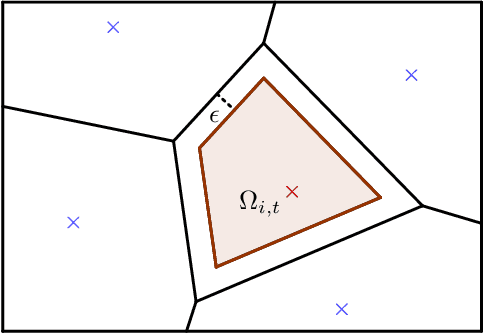
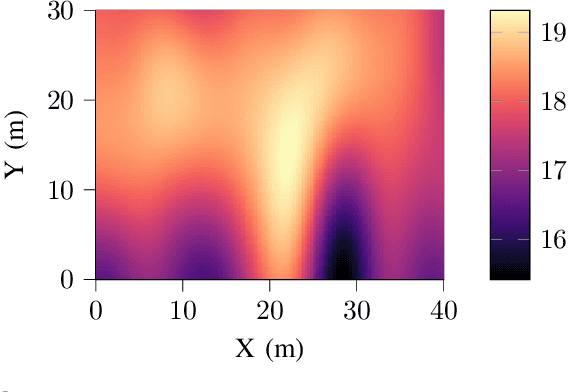
This paper discusses the adaptive sampling problem in a nonholonomic mobile robotic sensor network for efficiently monitoring a spatial field. It is proposed to employ Gaussian process to model a spatial phenomenon and predict it at unmeasured positions, which enables the sampling optimization problem to be formulated by the use of the log determinant of a predicted covariance matrix at next sampling locations. The control, movement and nonholonomic dynamics constraints of the mobile sensors are also considered in the adaptive sampling optimization problem. In order to tackle the nonlinearity and nonconvexity of the objective function in the optimization problem we first exploit the linearized alternating direction method of multipliers (L-ADMM) method that can effectively simplify the objective function, though it is computationally expensive since a nonconvex problem needs to be solved exactly in each iteration. We then propose a novel approach called the successive convexified ADMM (SC-ADMM) that sequentially convexify the nonlinear dynamic constraints so that the original optimization problem can be split into convex subproblems. It is noted that both the L-ADMM algorithm and our SC-ADMM approach can solve the sampling optimization problem in either a centralized or a distributed manner. We validated the proposed approaches in 1000 experiments in a synthetic environment with a real-world dataset, where the obtained results suggest that both the L-ADMM and SC- ADMM techniques can provide good accuracy for the monitoring purpose. However, our proposed SC-ADMM approach computationally outperforms the L-ADMM counterpart, demonstrating its better practicality.