Reflections from the 2024 Large Language Model (LLM) Hackathon for Applications in Materials Science and Chemistry

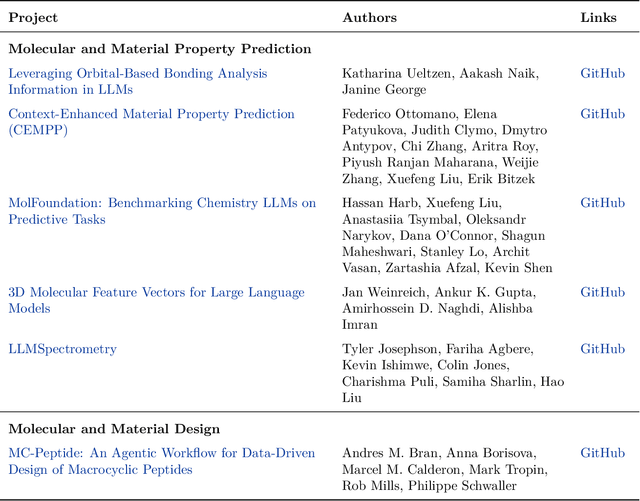
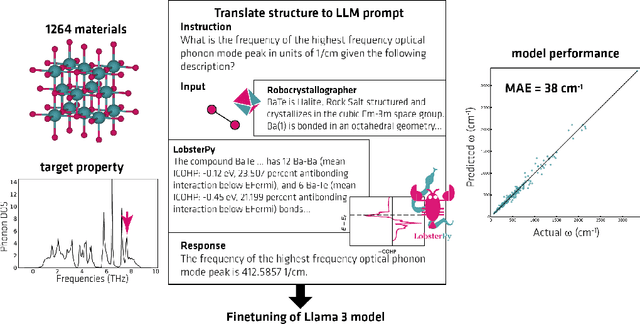
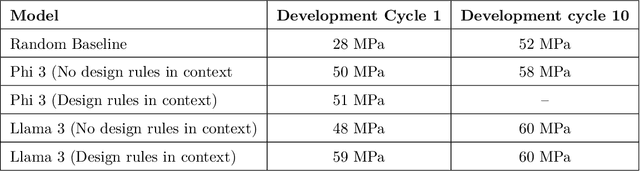
Here, we present the outcomes from the second Large Language Model (LLM) Hackathon for Applications in Materials Science and Chemistry, which engaged participants across global hybrid locations, resulting in 34 team submissions. The submissions spanned seven key application areas and demonstrated the diverse utility of LLMs for applications in (1) molecular and material property prediction; (2) molecular and material design; (3) automation and novel interfaces; (4) scientific communication and education; (5) research data management and automation; (6) hypothesis generation and evaluation; and (7) knowledge extraction and reasoning from scientific literature. Each team submission is presented in a summary table with links to the code and as brief papers in the appendix. Beyond team results, we discuss the hackathon event and its hybrid format, which included physical hubs in Toronto, Montreal, San Francisco, Berlin, Lausanne, and Tokyo, alongside a global online hub to enable local and virtual collaboration. Overall, the event highlighted significant improvements in LLM capabilities since the previous year's hackathon, suggesting continued expansion of LLMs for applications in materials science and chemistry research. These outcomes demonstrate the dual utility of LLMs as both multipurpose models for diverse machine learning tasks and platforms for rapid prototyping custom applications in scientific research.

Latent Linear Quadratic Regulator for Robotic Control Tasks

Model predictive control (MPC) has played a more crucial role in various robotic control tasks, but its high computational requirements are concerning, especially for nonlinear dynamical models. This paper presents a $\textbf{la}$tent $\textbf{l}$inear $\textbf{q}$uadratic $\textbf{r}$egulator (LaLQR) that maps the state space into a latent space, on which the dynamical model is linear and the cost function is quadratic, allowing the efficient application of LQR. We jointly learn this alternative system by imitating the original MPC. Experiments show LaLQR's superior efficiency and generalization compared to other baselines.

Physics-Informed Machine Learning for Modeling and Control of Dynamical Systems

Physics-informed machine learning (PIML) is a set of methods and tools that systematically integrate machine learning (ML) algorithms with physical constraints and abstract mathematical models developed in scientific and engineering domains. As opposed to purely data-driven methods, PIML models can be trained from additional information obtained by enforcing physical laws such as energy and mass conservation. More broadly, PIML models can include abstract properties and conditions such as stability, convexity, or invariance. The basic premise of PIML is that the integration of ML and physics can yield more effective, physically consistent, and data-efficient models. This paper aims to provide a tutorial-like overview of the recent advances in PIML for dynamical system modeling and control. Specifically, the paper covers an overview of the theory, fundamental concepts and methods, tools, and applications on topics of: 1) physics-informed learning for system identification; 2) physics-informed learning for control; 3) analysis and verification of PIML models; and 4) physics-informed digital twins. The paper is concluded with a perspective on open challenges and future research opportunities.

Distributed Model Predictive Control of Buildings and Energy Hubs

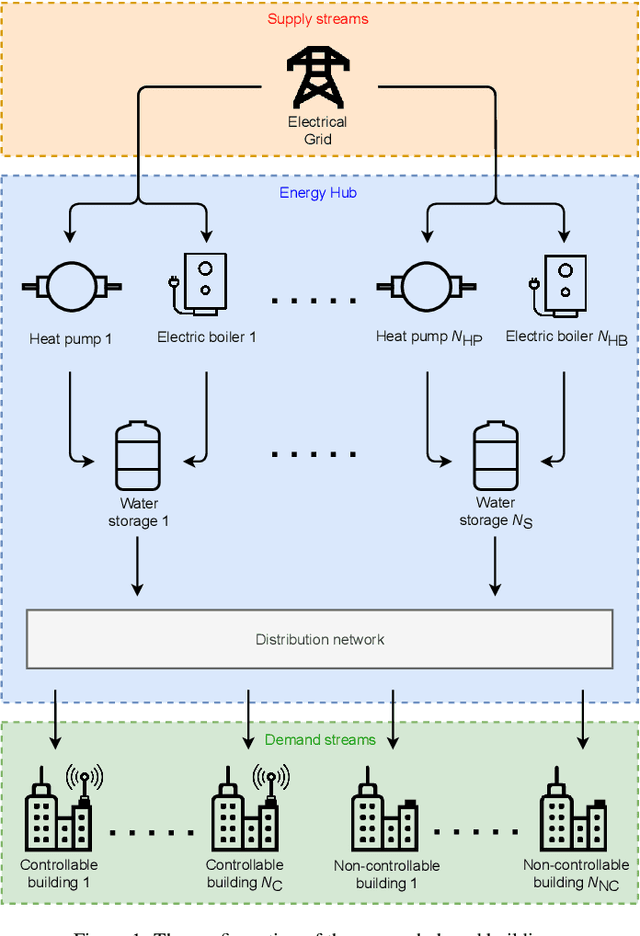
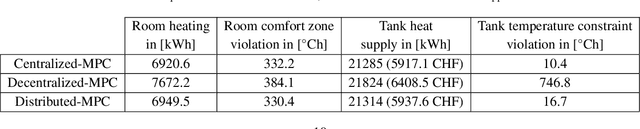
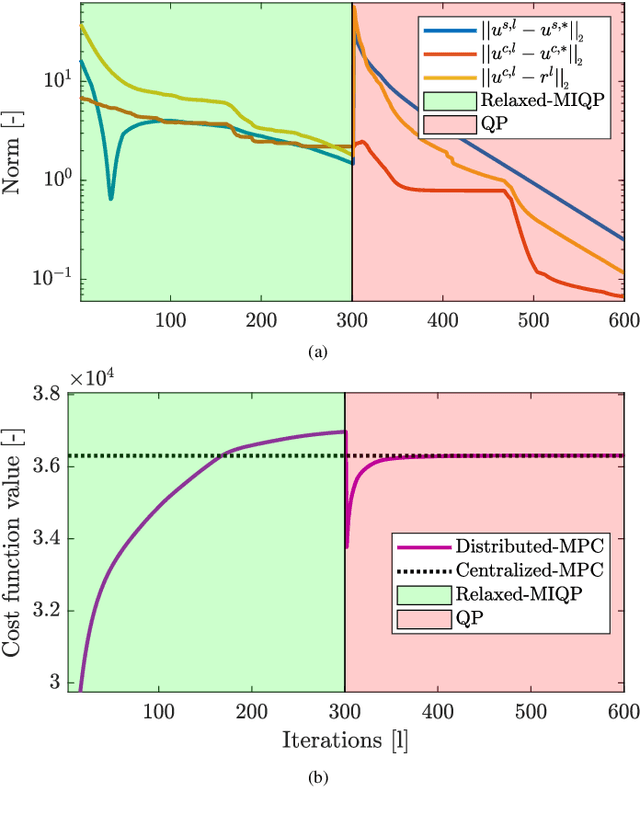
Model predictive control (MPC) strategies can be applied to the coordination of energy hubs to reduce their energy consumption. Despite the effectiveness of these techniques, their potential for energy savings are potentially underutilized due to the fact that energy demands are often assumed to be fixed quantities rather than controlled dynamic variables. The joint optimization of energy hubs and buildings' energy management systems can result in higher energy savings. This paper investigates how different MPC strategies perform on energy management systems in buildings and energy hubs. We first discuss two MPC approaches; centralized and decentralized. While the centralized control strategy offers optimal performance, its implementation is computationally prohibitive and raises privacy concerns. On the other hand, the decentralized control approach, which offers ease of implementation, displays significantly lower performance. We propose a third strategy, distributed control based on dual decomposition, which has the advantages of both approaches. Numerical case studies and comparisons demonstrate that the performance of distributed control is close to the performance of the centralized case, while maintaining a significantly lower computational burden, especially in large-scale scenarios with many agents. Finally, we validate and verify the reliability of the proposed method through an experiment on a full-scale energy hub system in the NEST demonstrator in D\"{u}bendorf, Switzerland.

A Generalized Representer Theorem for Hilbert Space - Valued Functions

The necessary and sufficient conditions for existence of a generalized representer theorem are presented for learning Hilbert space-valued functions. Representer theorems involving explicit basis functions and Reproducing Kernels are a common occurrence in various machine learning algorithms like generalized least squares, support vector machines, Gaussian process regression and kernel based deep neural networks to name a few. Due to the more general structure of the underlying variational problems, the theory is also relevant to other application areas like optimal control, signal processing and decision making. We present the generalized representer as a unified view for supervised and semi-supervised learning methods, using the theory of linear operators and subspace valued maps. The implications of the theorem are presented with examples of multi input-multi output regression, kernel based deep neural networks, stochastic regression and sparsity learning problems as being special cases in this unified view.