Latent Linear Quadratic Regulator for Robotic Control Tasks

Model predictive control (MPC) has played a more crucial role in various robotic control tasks, but its high computational requirements are concerning, especially for nonlinear dynamical models. This paper presents a $\textbf{la}$tent $\textbf{l}$inear $\textbf{q}$uadratic $\textbf{r}$egulator (LaLQR) that maps the state space into a latent space, on which the dynamical model is linear and the cost function is quadratic, allowing the efficient application of LQR. We jointly learn this alternative system by imitating the original MPC. Experiments show LaLQR's superior efficiency and generalization compared to other baselines.

STLCCP: An Efficient Convex Optimization-based Framework for Signal Temporal Logic Specifications

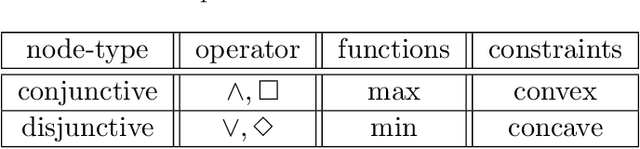
Signal Temporal Logic (STL) is capable of expressing a broad range of temporal properties that controlled dynamical systems must satisfy. In the literature, both mixed-integer programming (MIP) and nonlinear programming (NLP) methods have been applied to solve optimal control problems with STL specifications. However, neither approach has succeeded in solving problems with complex long-horizon STL specifications within a realistic timeframe. This study proposes a new optimization framework, called \textit{STLCCP}, which explicitly incorporates several structures of STL to mitigate this issue. The core of our framework is a structure-aware decomposition of STL formulas, which converts the original program into a difference of convex (DC) programs. This program is then solved as a convex quadratic program sequentially, based on the convex-concave procedure (CCP). Our numerical experiments on several commonly used benchmarks demonstrate that this framework can effectively handle complex scenarios over long horizons, which have been challenging to address even using state-of-the-art optimization methods.

Signal Temporal Logic Meets Convex-Concave Programming: A Structure-Exploiting SQP Algorithm for STL Specifications

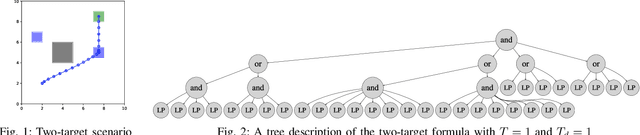
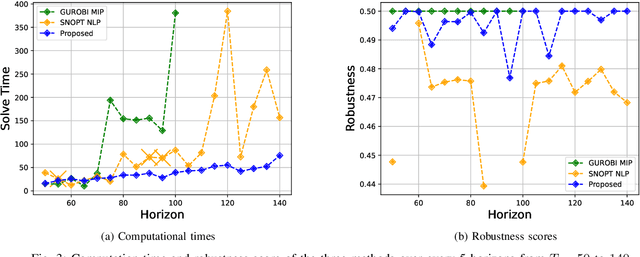
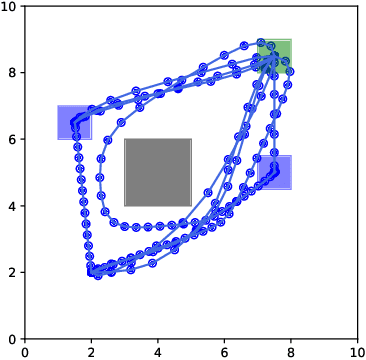
This study considers the control problem with signal temporal logic (STL) specifications. Prior works have adopted smoothing techniques to address this problem within a feasible time frame and solve the problem by applying sequential quadratic programming (SQP) methods naively. However, one of the drawbacks of this approach is that solutions can easily become trapped in local minima that do not satisfy the specification. In this study, we propose a new optimization method, termed CCP-based SQP, based on the convex-concave procedure (CCP). Our framework includes a new robustness decomposition method that decomposes the robustness function into a set of constraints, resulting in a form of difference of convex (DC) program that can be solved efficiently. We solve this DC program sequentially as a quadratic program by only approximating the disjunctive parts of the specifications. Our experimental results demonstrate that our method has a superior performance compared to the state-of-the-art SQP methods in terms of both robustness and computational time.

Whole-body model predictive control with rigid contacts via online switching time optimization

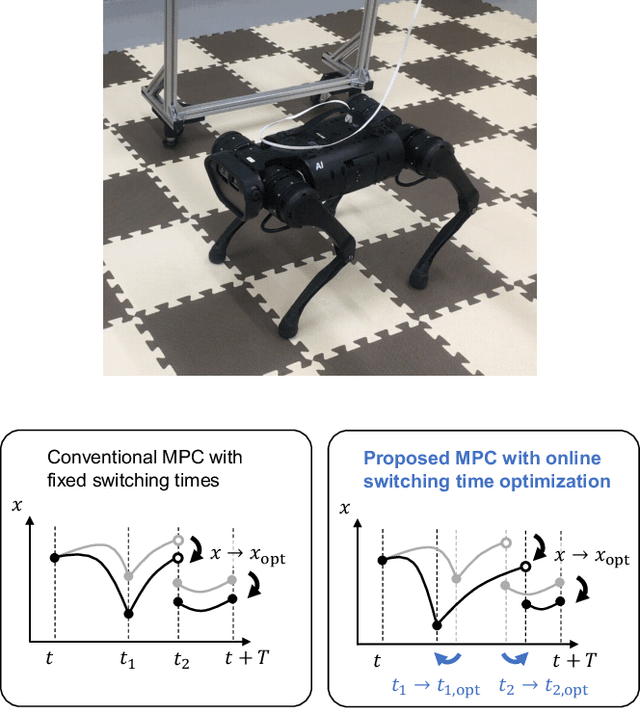
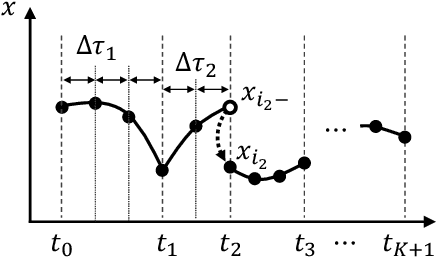
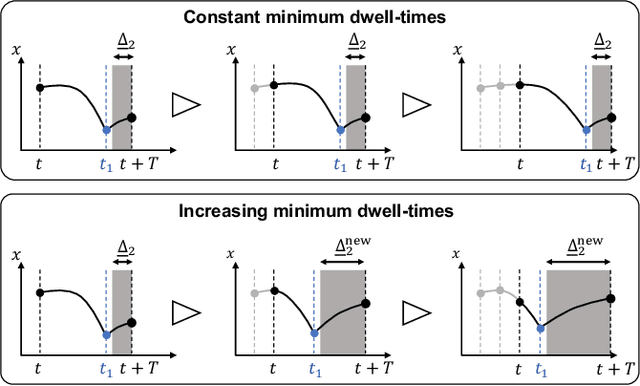
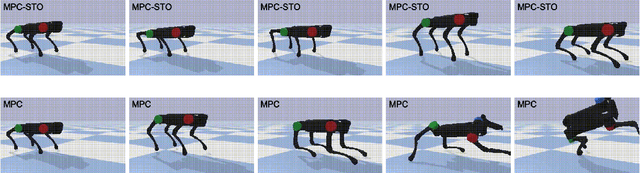
This study presents a whole-body model predictive control (MPC) of robotic systems with rigid contacts, under a given contact sequence using online switching time optimization (STO). We treat robot dynamics with rigid contacts as a switched system and formulate an optimal control problem of switched systems to implement the MPC. We utilize an efficient solution algorithm for the MPC problem that optimizes the switching times and trajectory simultaneously. The present efficient algorithm, unlike inefficient existing methods, enables online optimization as well as switching times. The proposed MPC with online STO is compared over the conventional MPC with fixed switching times, through numerical simulations of dynamic jumping motions of a quadruped robot. In the simulation comparison, the proposed MPC successfully controls the dynamic jumping motions in twice as many cases as the conventional MPC, which indicates that the proposed method extends the ability of the whole-body MPC. We further conduct hardware experiments on the quadrupedal robot Unitree A1 and prove that the proposed method achieves dynamic motions on the real robot.

Structure-Exploiting Newton-Type Method for Optimal Control of Switched Systems

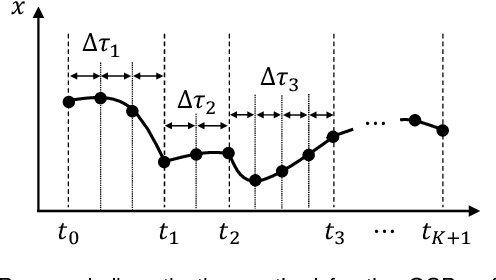
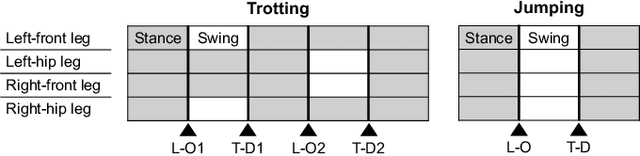
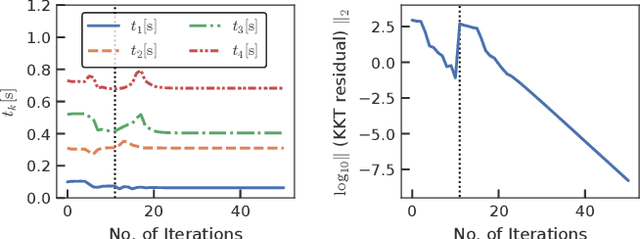
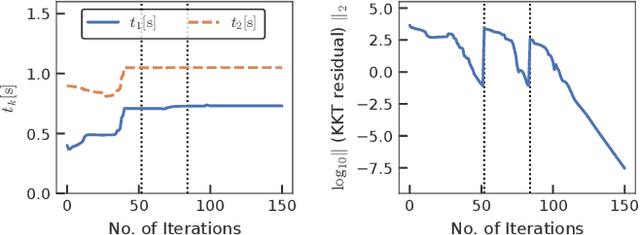
This study proposes an efficient Newton-type method for the optimal control of switched systems under a given mode sequence. A mesh-refinement-based approach is utilized to discretize continuous-time optimal control problems (OCPs) and formulate a nonlinear program (NLP), which guarantees the local convergence of a Newton-type method. A dedicated structure-exploiting algorithm (Riccati recursion) is proposed to perform a Newton-type method for the NLP efficiently because its sparsity structure is different from a standard OCP. The proposed method computes each Newton step with linear time-complexity for the total number of discretization grids as the standard Riccati recursion algorithm. Additionally, the computation is always successful if the solution is sufficiently close to a local minimum. Conversely, general quadratic programming (QP) solvers cannot accomplish this because the Hessian matrix is inherently indefinite. Moreover, a modification on the reduced Hessian matrix is proposed using the nature of the Riccati recursion algorithm as the dynamic programming for a QP subproblem to enhance the convergence. A numerical comparison is conducted with off-the-shelf NLP solvers, which demonstrates that the proposed method is up to two orders of magnitude faster. Whole-body optimal control of quadrupedal gaits is also demonstrated and shows that the proposed method can achieve the whole-body model predictive control (MPC) of robotic systems with rigid contacts.

Lifted contact dynamics for efficient direct optimal control of rigid body systems with contacts

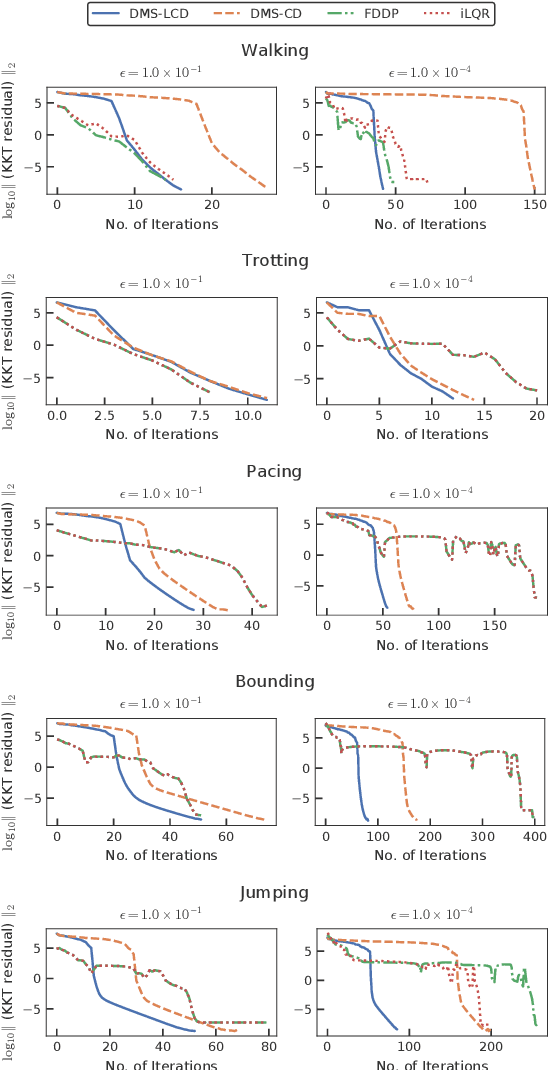
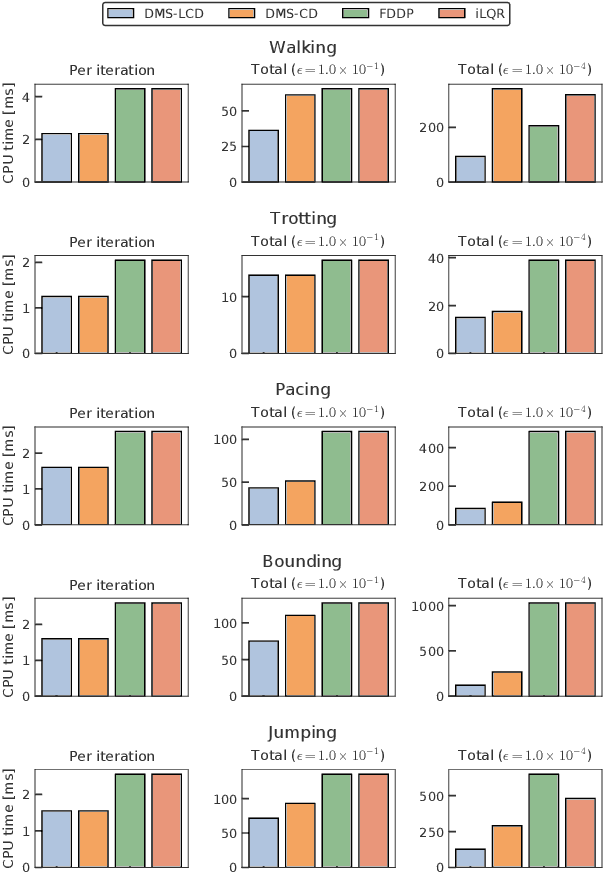
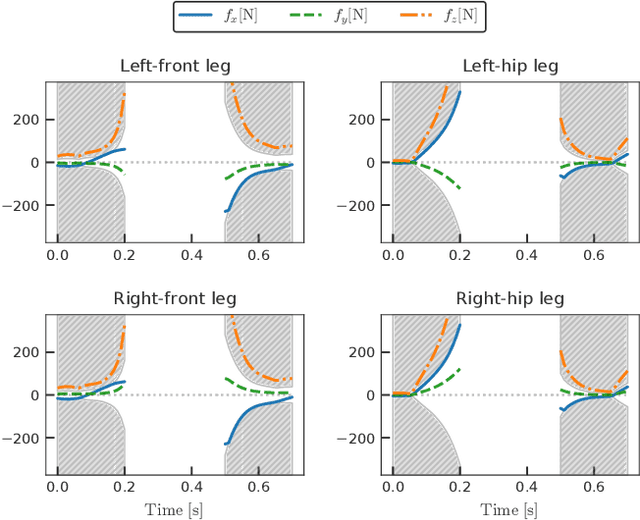
We propose a novel and efficient lifting approach for the direct optimal control of rigid-body systems with contacts to improve the convergence properties of Newton-type methods. To relax the high nonlinearity, we consider all variables, including the state, acceleration, contact forces, and control input torques, as optimization variables and the inverse dynamics and acceleration-level contact constraints as equality constraints. We eliminate the update of the acceleration, contact forces, and their dual variables from the linear equation to be solved in each Newton-type iteration in an efficient manner. As a result, the computational cost per Newton-type iteration is almost identical to that of the conventional non-lifted Newton-type iteration that embeds contact dynamics in the state equation. We conducted numerical experiments on the whole-body optimal control of various quadrupedal gaits subject to the friction cone constraints considered in interior-point methods and demonstrated that the proposed method can significantly increase the convergence speed to more than twice that of the conventional non-lifted approach.

Efficient solution method based on inverse dynamics for optimal control problems of rigid body systems

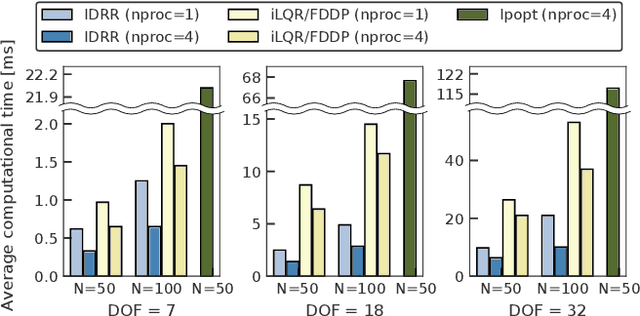
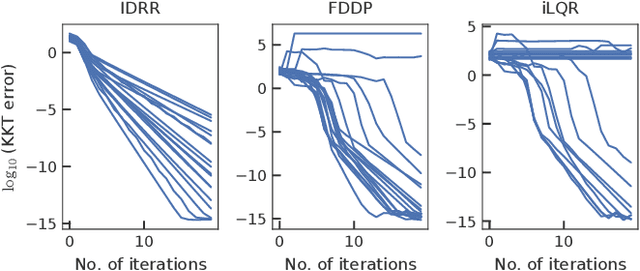
We propose an efficient way of solving optimal control problems for rigid-body systems on the basis of inverse dynamics and the multiple-shooting method. We treat all variables, including the state, acceleration, and control input torques, as optimization variables and treat the inverse dynamics as an equality constraint. We eliminate the update of the control input torques from the linear equation of Newton's method by applying condensing for inverse dynamics. The size of the resultant linear equation is the same as that of the multiple-shooting method based on forward dynamics except for the variables related to the passive joints and contacts. Compared with the conventional methods based on forward dynamics, the proposed method reduces the computational cost of the dynamics and their sensitivities by utilizing the recursive Newton-Euler algorithm (RNEA) and its partial derivatives. In addition, it increases the sparsity of the Hessian of the Karush-Kuhn-Tucker conditions, which reduces the computational cost, e.g., of Riccati recursion. Numerical experiments show that the proposed method outperforms state-of-the-art implementations of differential dynamic programming based on forward dynamics in terms of computational time and numerical robustness.

Bayesian filtering for nonlinear stochastic systems using holonomic gradient method with integral transform

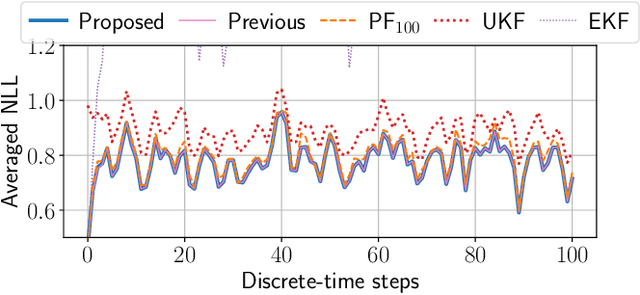
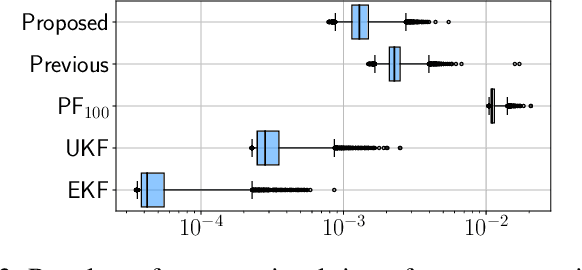
This paper proposes a symbolic-numeric Bayesian filtering method for a class of discrete-time nonlinear stochastic systems to achieve high accuracy with a relatively small online computational cost. The proposed method is based on the holonomic gradient method (HGM), which is a symbolic-numeric method to evaluate integrals efficiently depending on several parameters. By approximating the posterior probability density function (PDF) of the state as a Gaussian PDF, the update process of its mean and variance can be formulated as evaluations of several integrals that exactly take into account the nonlinearity of the system dynamics. An integral transform is used to evaluate these integrals more efficiently using the HGM than our previous method. Further, a numerical example is provided to demonstrate the efficiency of the proposed method compared to other existing methods.

Efficient Riccati recursion for optimal control problems with pure-state equality constraints

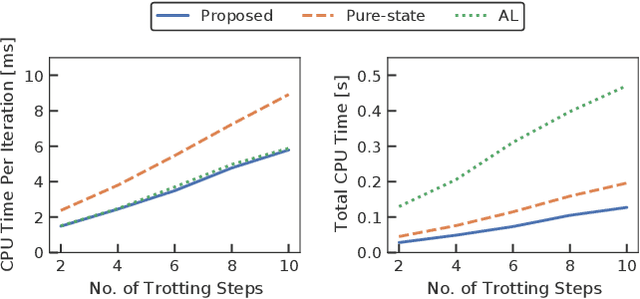
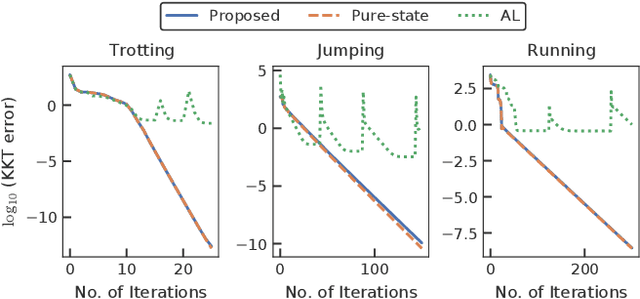
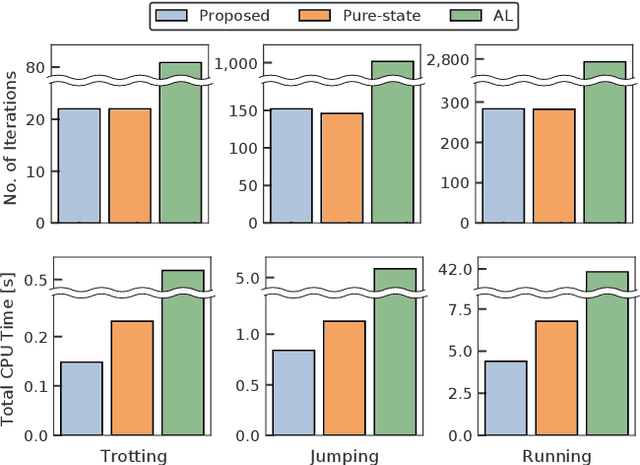
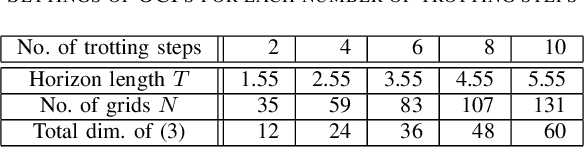
A novel approach to efficiently treat pure-state equality constraints in optimal control problems (OCPs) using a Riccati recursion algorithm is proposed. The proposed method transforms a pure-state equality constraint into a mixed state-control constraint such that the constraint is expressed by variables at a certain previous time stage. It is showed that if the solution satisfies the second-order sufficient conditions of the OCP with the transformed mixed state-control constraints, it is a local minimum of the OCP with the original pure-state constraints. A Riccati recursion algorithm is derived to solve the OCP using the transformed constraints with linear time complexity in the grid number of the horizon, in contrast to a previous approach that scales cubically with respect to the total dimension of the pure-state equality constraints. Numerical experiments on the whole-body optimal control of quadrupedal gaits that involve pure-state equality constraints owing to contact switches demonstrate the effectiveness of the proposed method over existing approaches.