Bayesian filtering for nonlinear stochastic systems using holonomic gradient method with integral transform
Paper and Code
Mar 03, 2021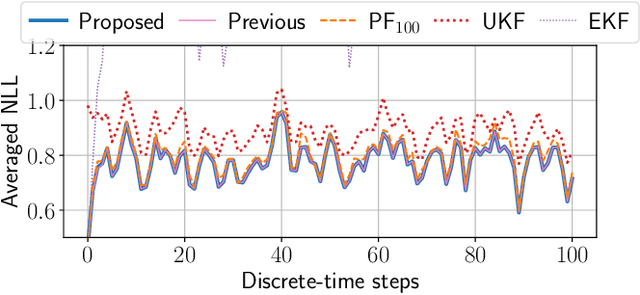
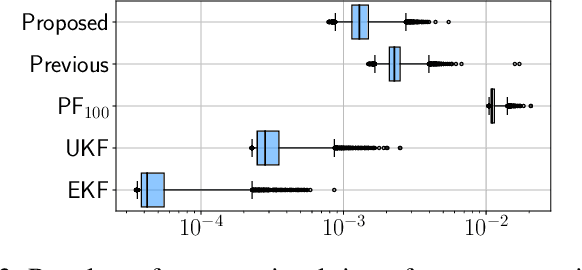
This paper proposes a symbolic-numeric Bayesian filtering method for a class of discrete-time nonlinear stochastic systems to achieve high accuracy with a relatively small online computational cost. The proposed method is based on the holonomic gradient method (HGM), which is a symbolic-numeric method to evaluate integrals efficiently depending on several parameters. By approximating the posterior probability density function (PDF) of the state as a Gaussian PDF, the update process of its mean and variance can be formulated as evaluations of several integrals that exactly take into account the nonlinearity of the system dynamics. An integral transform is used to evaluate these integrals more efficiently using the HGM than our previous method. Further, a numerical example is provided to demonstrate the efficiency of the proposed method compared to other existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge