Lifted contact dynamics for efficient direct optimal control of rigid body systems with contacts
Paper and Code
Aug 03, 2021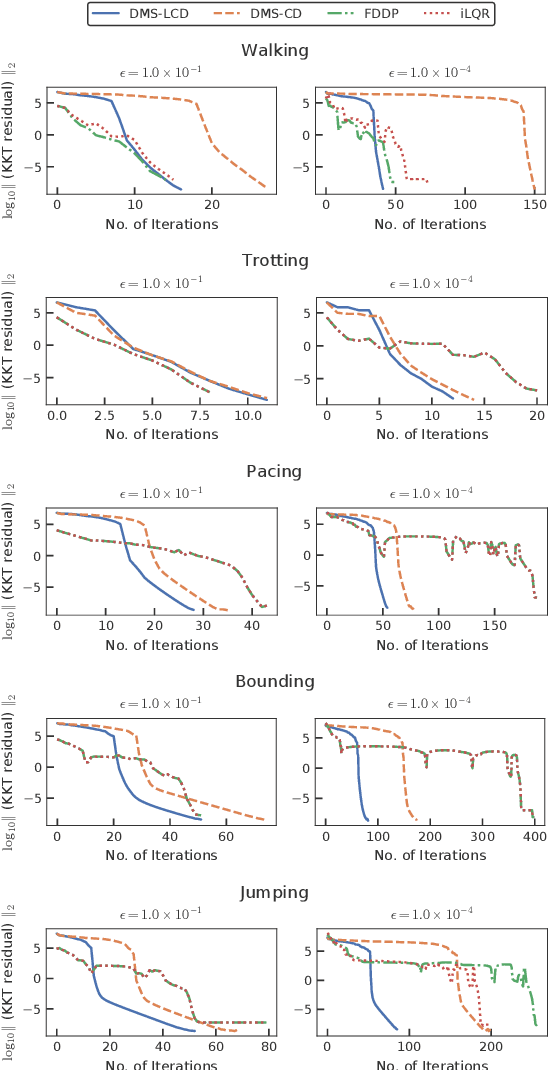
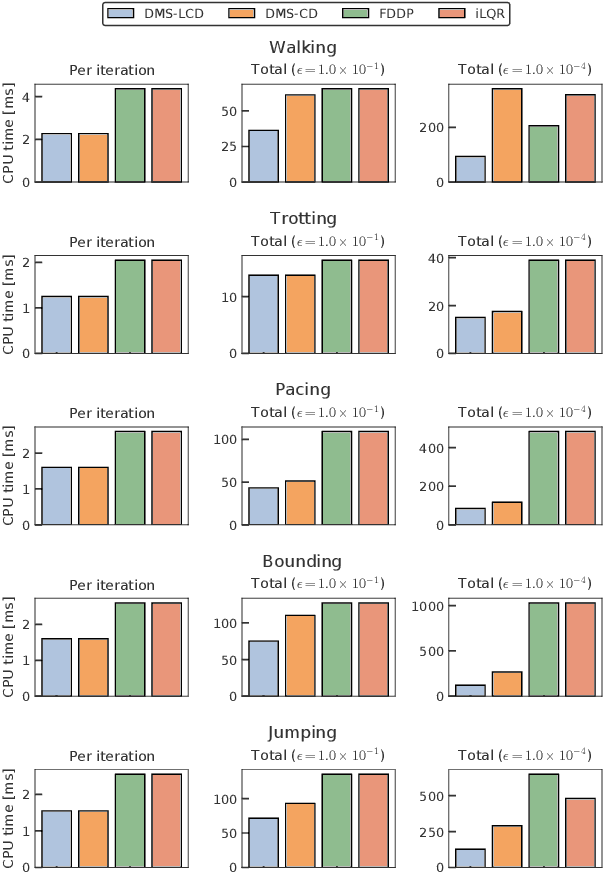

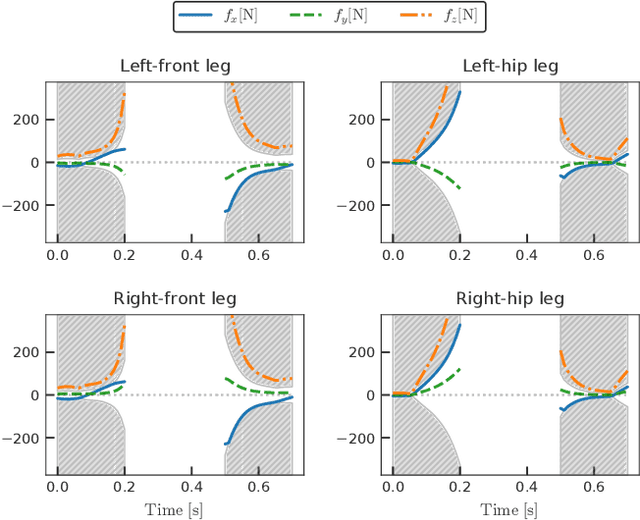
We propose a novel and efficient lifting approach for the direct optimal control of rigid-body systems with contacts to improve the convergence properties of Newton-type methods. To relax the high nonlinearity, we consider all variables, including the state, acceleration, contact forces, and control input torques, as optimization variables and the inverse dynamics and acceleration-level contact constraints as equality constraints. We eliminate the update of the acceleration, contact forces, and their dual variables from the linear equation to be solved in each Newton-type iteration in an efficient manner. As a result, the computational cost per Newton-type iteration is almost identical to that of the conventional non-lifted Newton-type iteration that embeds contact dynamics in the state equation. We conducted numerical experiments on the whole-body optimal control of various quadrupedal gaits subject to the friction cone constraints considered in interior-point methods and demonstrated that the proposed method can significantly increase the convergence speed to more than twice that of the conventional non-lifted approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge