Robust Locomotion via Zero-order Stochastic Nonlinear Model Predictive Control with Guard Saltation Matrix

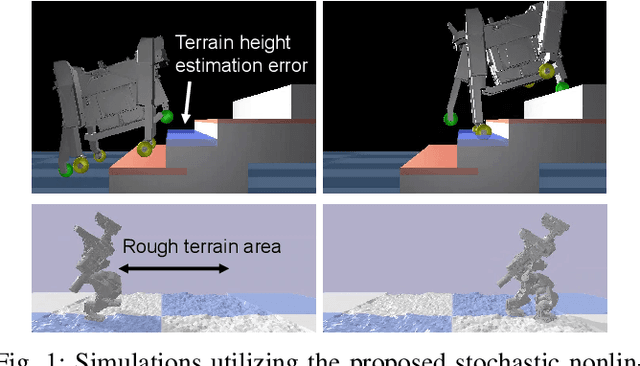
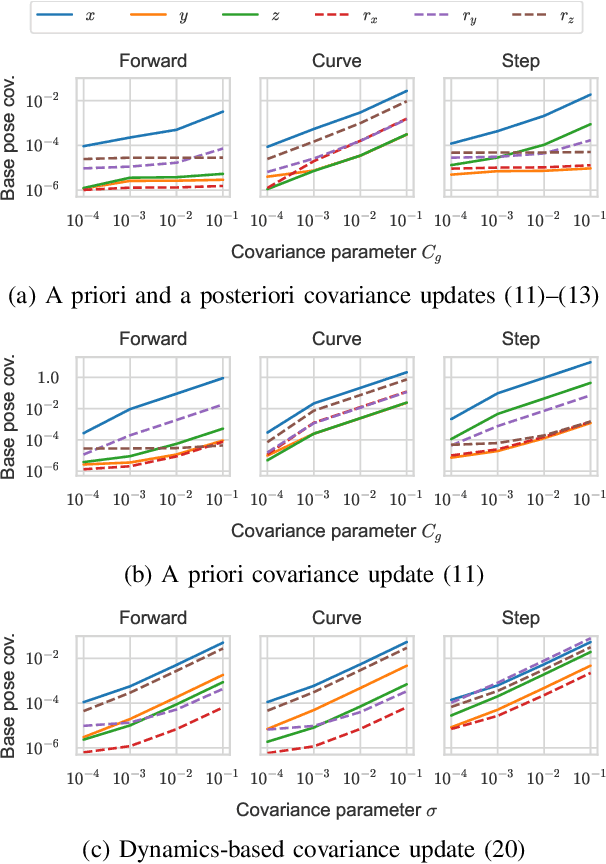
This paper presents a stochastic/robust nonlinear model predictive control (NMPC) to enhance the robustness of legged locomotion against contact uncertainties. We integrate the contact uncertainties into the covariance propagation of stochastic/robust NMPC framework by leveraging the guard saltation matrix and an extended Kalman filter-like covariance update. We achieve fast stochastic/robust NMPC computation by utilizing the zero-order stochastic/robust NMPC algorithm with additional improvements in computational efficiency concerning the feedback gains. We conducted numerical experiments and demonstrate that the proposed method can accurately forecast future state covariance and generate trajectories that satisfies constraints even in the presence of the contact uncertainties. Hardware experiments on the perceptive locomotion of a wheeled-legged robot were also carried out, validating the feasibility of the proposed method in a real-world system with limited on-board computation.

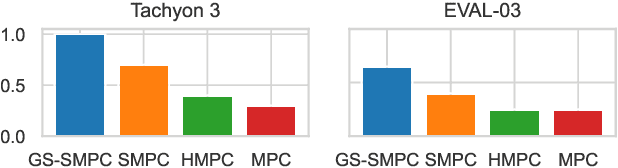
Versatile Telescopic-Wheeled-Legged Locomotion of Tachyon 3 via Full-Centroidal Nonlinear Model Predictive Control

This paper presents a nonlinear model predictive control (NMPC) toward versatile motion generation for the telescopic-wheeled-legged robot Tachyon 3, the unique hardware structure of which poses challenges in control and motion planning. We apply the full-centroidal NMPC formulation with dedicated constraints that can capture the accurate kinematics and dynamics of Tachyon 3. We have developed a control pipeline that includes an internal state integrator to apply NMPC to Tachyon 3, the actuators of which employ high-gain position-controllers. We conducted simulation and hardware experiments on the perceptive locomotion of Tachyon 3 over structured terrains and demonstrated that the proposed method can achieve smooth and dynamic motion generation under harsh physical and environmental constraints.

Quasistatic contact-rich manipulation via linear complementarity quadratic programming

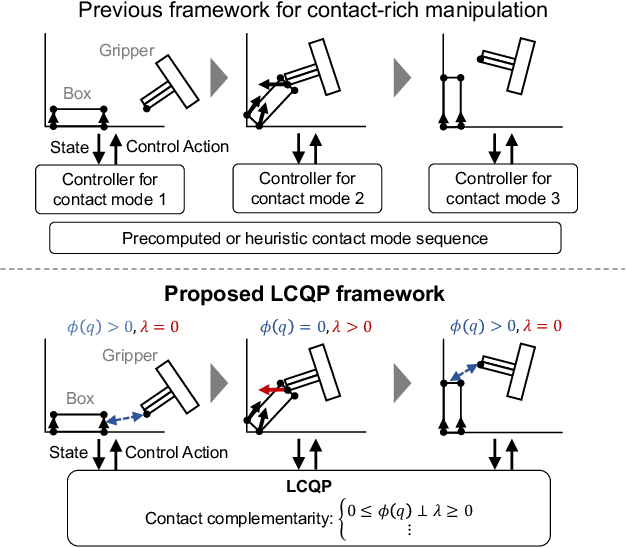
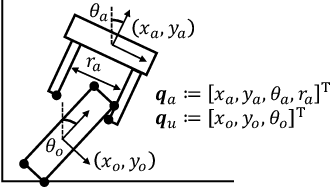
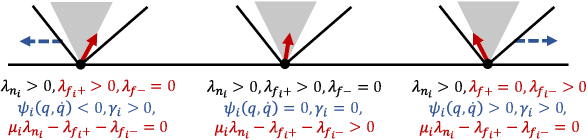
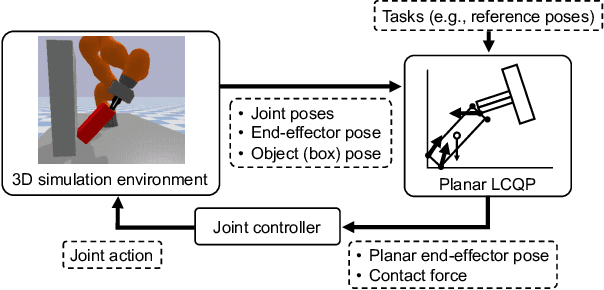
Contact-rich manipulation is challenging due to dynamically-changing physical constraints by the contact mode changes undergone during manipulation. This paper proposes a versatile local planning and control framework for contact-rich manipulation that determines the continuous control action under variable contact modes online. We model the physical characteristics of contact-rich manipulation by quasistatic dynamics and complementarity constraints. We then propose a linear complementarity quadratic program (LCQP) to efficiently determine the control action that implicitly includes the decisions on the contact modes under these constraints. In the LCQP, we relax the complementarity constraints to alleviate ill-conditioned problems that are typically caused by measure noises or model miss-matches. We conduct dynamical simulations on a 3D physical simulator and demonstrate that the proposed method can achieve various contact-rich manipulation tasks by determining the control action including the contact modes in real-time.

Whole-body model predictive control with rigid contacts via online switching time optimization

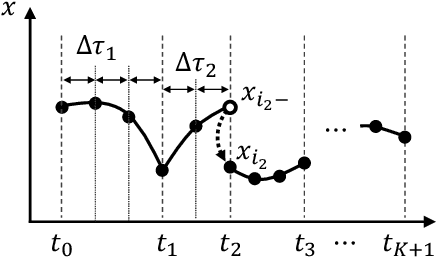
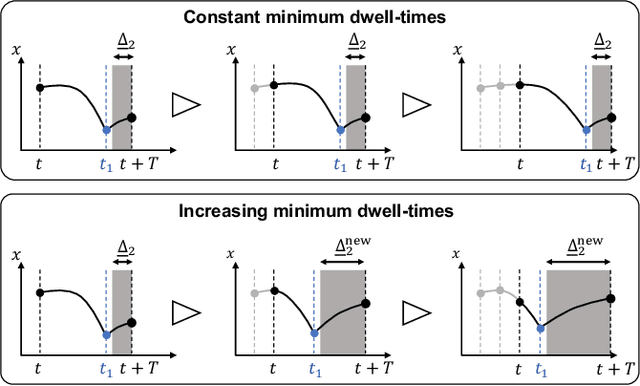
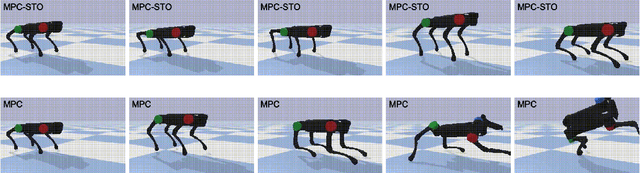
This study presents a whole-body model predictive control (MPC) of robotic systems with rigid contacts, under a given contact sequence using online switching time optimization (STO). We treat robot dynamics with rigid contacts as a switched system and formulate an optimal control problem of switched systems to implement the MPC. We utilize an efficient solution algorithm for the MPC problem that optimizes the switching times and trajectory simultaneously. The present efficient algorithm, unlike inefficient existing methods, enables online optimization as well as switching times. The proposed MPC with online STO is compared over the conventional MPC with fixed switching times, through numerical simulations of dynamic jumping motions of a quadruped robot. In the simulation comparison, the proposed MPC successfully controls the dynamic jumping motions in twice as many cases as the conventional MPC, which indicates that the proposed method extends the ability of the whole-body MPC. We further conduct hardware experiments on the quadrupedal robot Unitree A1 and prove that the proposed method achieves dynamic motions on the real robot.

Structure-Exploiting Newton-Type Method for Optimal Control of Switched Systems

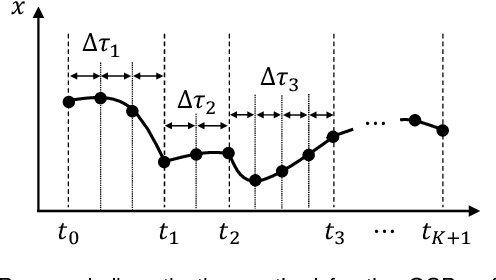
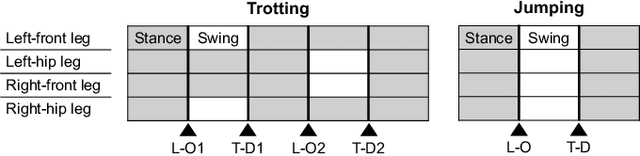
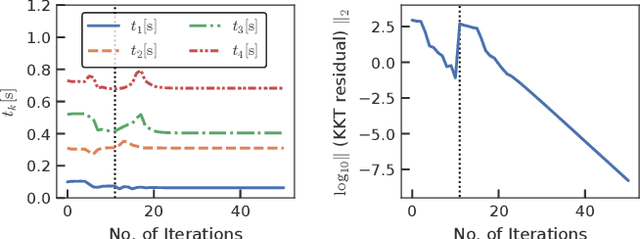
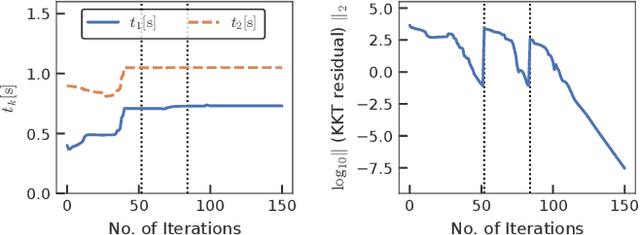
This study proposes an efficient Newton-type method for the optimal control of switched systems under a given mode sequence. A mesh-refinement-based approach is utilized to discretize continuous-time optimal control problems (OCPs) and formulate a nonlinear program (NLP), which guarantees the local convergence of a Newton-type method. A dedicated structure-exploiting algorithm (Riccati recursion) is proposed to perform a Newton-type method for the NLP efficiently because its sparsity structure is different from a standard OCP. The proposed method computes each Newton step with linear time-complexity for the total number of discretization grids as the standard Riccati recursion algorithm. Additionally, the computation is always successful if the solution is sufficiently close to a local minimum. Conversely, general quadratic programming (QP) solvers cannot accomplish this because the Hessian matrix is inherently indefinite. Moreover, a modification on the reduced Hessian matrix is proposed using the nature of the Riccati recursion algorithm as the dynamic programming for a QP subproblem to enhance the convergence. A numerical comparison is conducted with off-the-shelf NLP solvers, which demonstrates that the proposed method is up to two orders of magnitude faster. Whole-body optimal control of quadrupedal gaits is also demonstrated and shows that the proposed method can achieve the whole-body model predictive control (MPC) of robotic systems with rigid contacts.

Lifted contact dynamics for efficient direct optimal control of rigid body systems with contacts

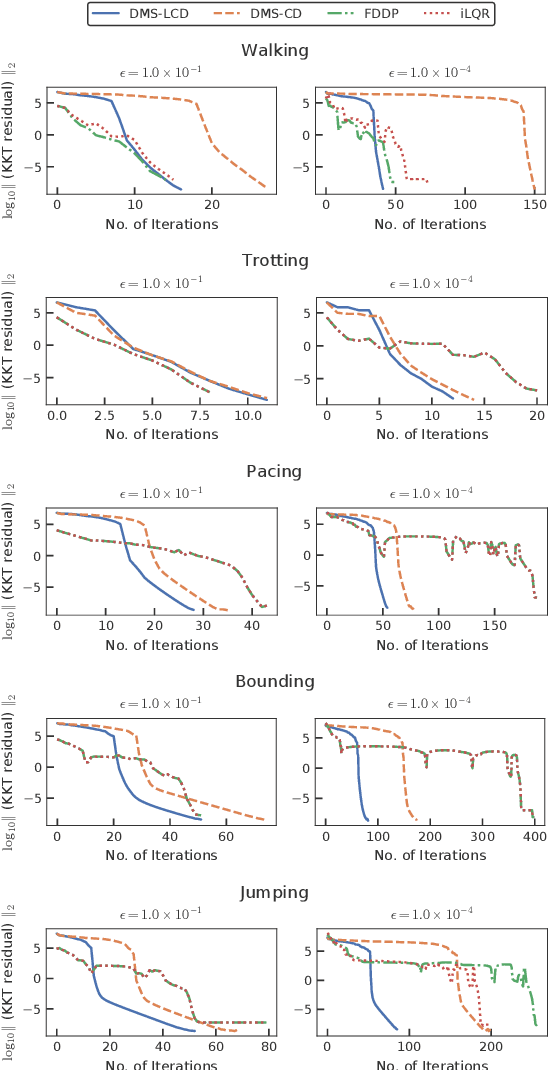
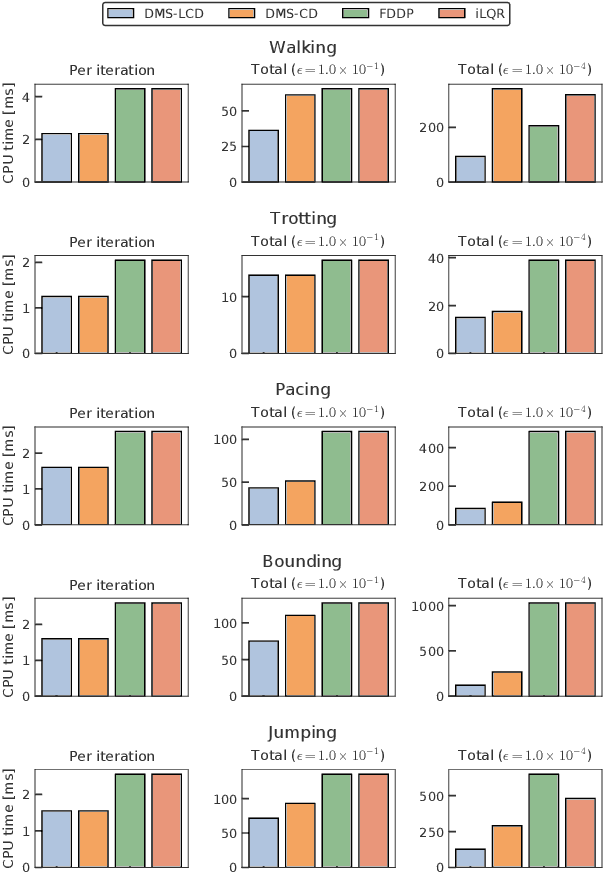
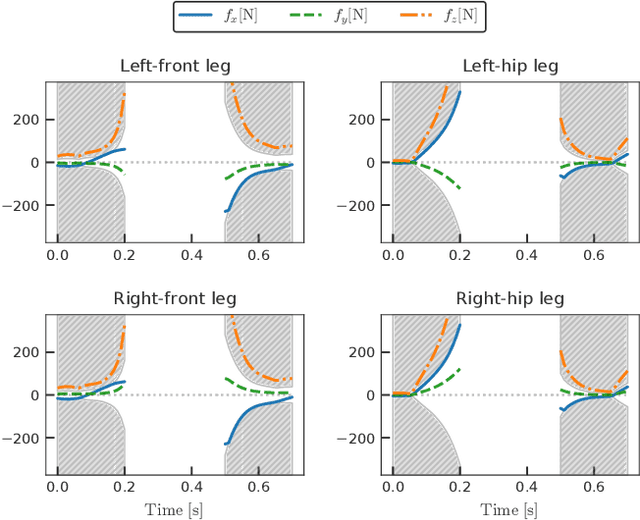
We propose a novel and efficient lifting approach for the direct optimal control of rigid-body systems with contacts to improve the convergence properties of Newton-type methods. To relax the high nonlinearity, we consider all variables, including the state, acceleration, contact forces, and control input torques, as optimization variables and the inverse dynamics and acceleration-level contact constraints as equality constraints. We eliminate the update of the acceleration, contact forces, and their dual variables from the linear equation to be solved in each Newton-type iteration in an efficient manner. As a result, the computational cost per Newton-type iteration is almost identical to that of the conventional non-lifted Newton-type iteration that embeds contact dynamics in the state equation. We conducted numerical experiments on the whole-body optimal control of various quadrupedal gaits subject to the friction cone constraints considered in interior-point methods and demonstrated that the proposed method can significantly increase the convergence speed to more than twice that of the conventional non-lifted approach.

Efficient solution method based on inverse dynamics for optimal control problems of rigid body systems

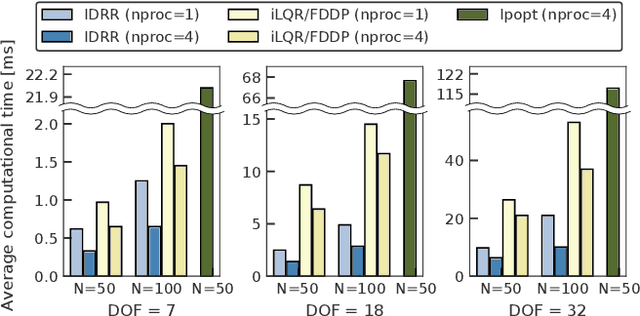
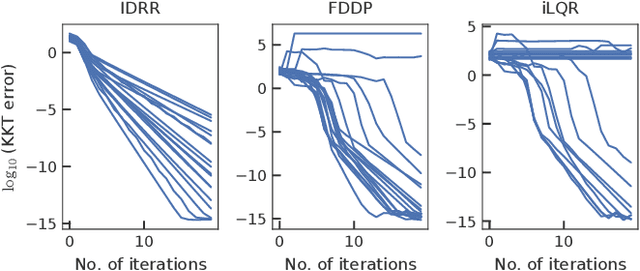
We propose an efficient way of solving optimal control problems for rigid-body systems on the basis of inverse dynamics and the multiple-shooting method. We treat all variables, including the state, acceleration, and control input torques, as optimization variables and treat the inverse dynamics as an equality constraint. We eliminate the update of the control input torques from the linear equation of Newton's method by applying condensing for inverse dynamics. The size of the resultant linear equation is the same as that of the multiple-shooting method based on forward dynamics except for the variables related to the passive joints and contacts. Compared with the conventional methods based on forward dynamics, the proposed method reduces the computational cost of the dynamics and their sensitivities by utilizing the recursive Newton-Euler algorithm (RNEA) and its partial derivatives. In addition, it increases the sparsity of the Hessian of the Karush-Kuhn-Tucker conditions, which reduces the computational cost, e.g., of Riccati recursion. Numerical experiments show that the proposed method outperforms state-of-the-art implementations of differential dynamic programming based on forward dynamics in terms of computational time and numerical robustness.

Efficient Riccati recursion for optimal control problems with pure-state equality constraints

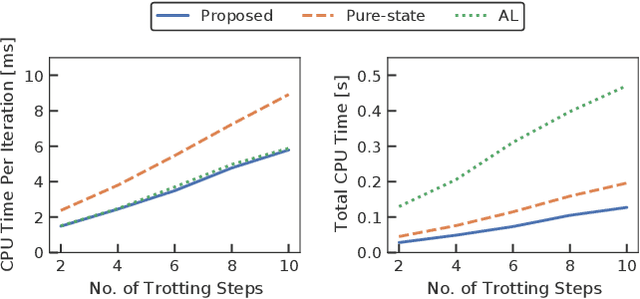
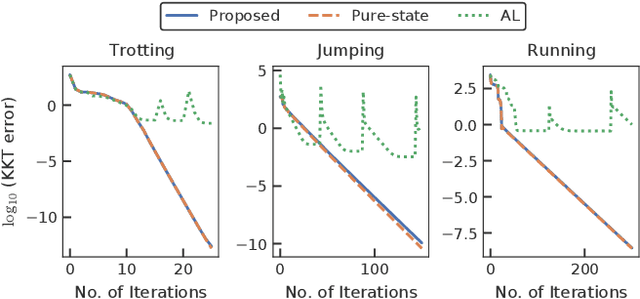
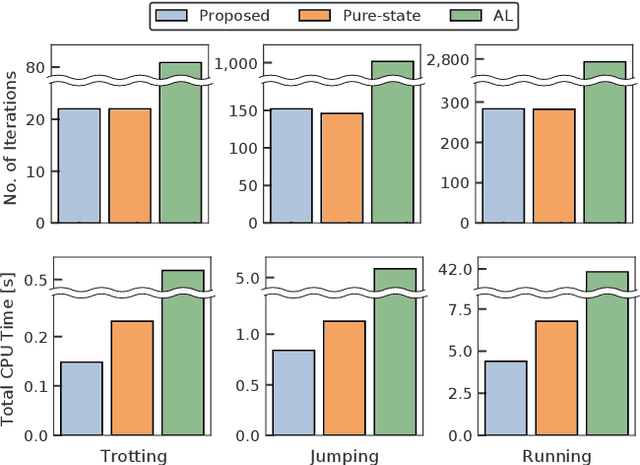
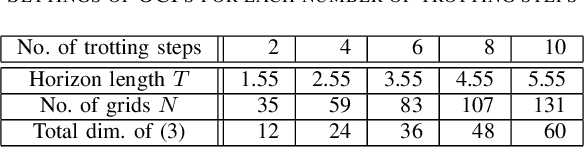
A novel approach to efficiently treat pure-state equality constraints in optimal control problems (OCPs) using a Riccati recursion algorithm is proposed. The proposed method transforms a pure-state equality constraint into a mixed state-control constraint such that the constraint is expressed by variables at a certain previous time stage. It is showed that if the solution satisfies the second-order sufficient conditions of the OCP with the transformed mixed state-control constraints, it is a local minimum of the OCP with the original pure-state constraints. A Riccati recursion algorithm is derived to solve the OCP using the transformed constraints with linear time complexity in the grid number of the horizon, in contrast to a previous approach that scales cubically with respect to the total dimension of the pure-state equality constraints. Numerical experiments on the whole-body optimal control of quadrupedal gaits that involve pure-state equality constraints owing to contact switches demonstrate the effectiveness of the proposed method over existing approaches.