STLCCP: An Efficient Convex Optimization-based Framework for Signal Temporal Logic Specifications

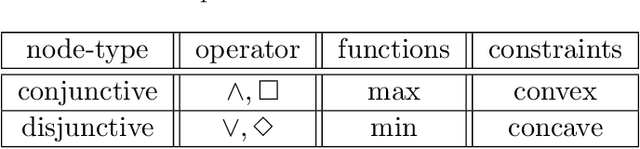
Signal Temporal Logic (STL) is capable of expressing a broad range of temporal properties that controlled dynamical systems must satisfy. In the literature, both mixed-integer programming (MIP) and nonlinear programming (NLP) methods have been applied to solve optimal control problems with STL specifications. However, neither approach has succeeded in solving problems with complex long-horizon STL specifications within a realistic timeframe. This study proposes a new optimization framework, called \textit{STLCCP}, which explicitly incorporates several structures of STL to mitigate this issue. The core of our framework is a structure-aware decomposition of STL formulas, which converts the original program into a difference of convex (DC) programs. This program is then solved as a convex quadratic program sequentially, based on the convex-concave procedure (CCP). Our numerical experiments on several commonly used benchmarks demonstrate that this framework can effectively handle complex scenarios over long horizons, which have been challenging to address even using state-of-the-art optimization methods.

Signal Temporal Logic Meets Convex-Concave Programming: A Structure-Exploiting SQP Algorithm for STL Specifications

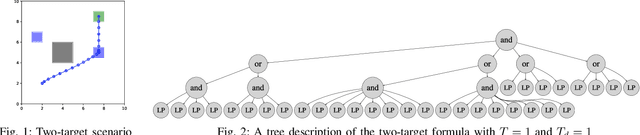
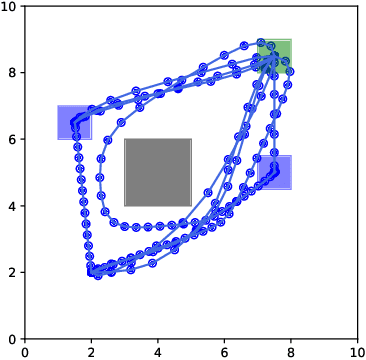
This study considers the control problem with signal temporal logic (STL) specifications. Prior works have adopted smoothing techniques to address this problem within a feasible time frame and solve the problem by applying sequential quadratic programming (SQP) methods naively. However, one of the drawbacks of this approach is that solutions can easily become trapped in local minima that do not satisfy the specification. In this study, we propose a new optimization method, termed CCP-based SQP, based on the convex-concave procedure (CCP). Our framework includes a new robustness decomposition method that decomposes the robustness function into a set of constraints, resulting in a form of difference of convex (DC) program that can be solved efficiently. We solve this DC program sequentially as a quadratic program by only approximating the disjunctive parts of the specifications. Our experimental results demonstrate that our method has a superior performance compared to the state-of-the-art SQP methods in terms of both robustness and computational time.