Physics-Informed Machine Learning for Modeling and Control of Dynamical Systems

Physics-informed machine learning (PIML) is a set of methods and tools that systematically integrate machine learning (ML) algorithms with physical constraints and abstract mathematical models developed in scientific and engineering domains. As opposed to purely data-driven methods, PIML models can be trained from additional information obtained by enforcing physical laws such as energy and mass conservation. More broadly, PIML models can include abstract properties and conditions such as stability, convexity, or invariance. The basic premise of PIML is that the integration of ML and physics can yield more effective, physically consistent, and data-efficient models. This paper aims to provide a tutorial-like overview of the recent advances in PIML for dynamical system modeling and control. Specifically, the paper covers an overview of the theory, fundamental concepts and methods, tools, and applications on topics of: 1) physics-informed learning for system identification; 2) physics-informed learning for control; 3) analysis and verification of PIML models; and 4) physics-informed digital twins. The paper is concluded with a perspective on open challenges and future research opportunities.

Stability Verification of Neural Network Controllers using Mixed-Integer Programming

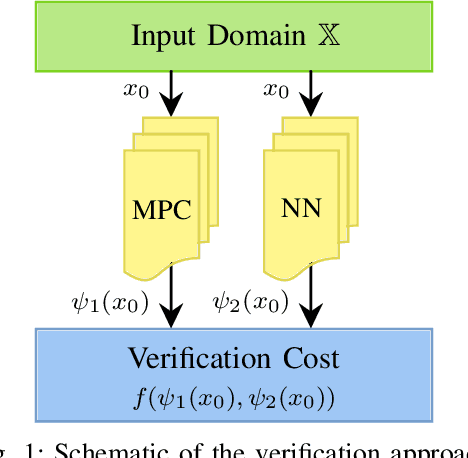
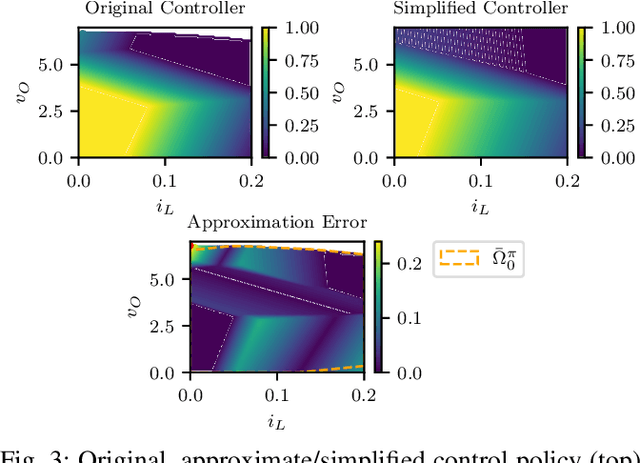
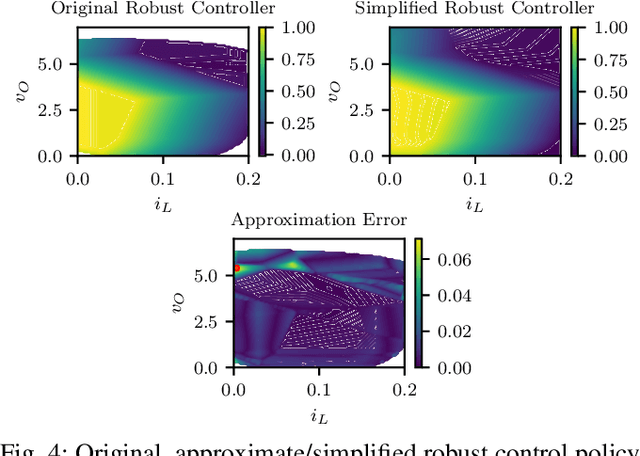
We propose a framework for the stability verification of Mixed-Integer Linear Programming (MILP) representable control policies. This framework compares a fixed candidate policy, which admits an efficient parameterization and can be evaluated at a low computational cost, against a fixed baseline policy, which is known to be stable but expensive to evaluate. We provide sufficient conditions for the closed-loop stability of the candidate policy in terms of the worst-case approximation error with respect to the baseline policy, and we show that these conditions can be checked by solving a Mixed-Integer Quadratic Program (MIQP). Additionally, we demonstrate that an outer approximation of the stability region of the candidate policy can be computed by solving an MILP. The proposed framework is sufficiently general to accommodate a broad range of candidate policies including ReLU Neural Networks (NNs), optimal solution maps of parametric quadratic programs, and Model Predictive Control (MPC) policies. We also present an open-source toolbox in Python based on the proposed framework, which allows for the easy verification of custom NN architectures and MPC formulations. We showcase the flexibility and reliability of our framework in the context of a DC-DC power convertor case study and investigate the computational complexity.