Bayesian Optimization of Partially Known Systems using Hybrid Models

Bayesian optimization (BO) has gained attention as an efficient algorithm for black-box optimization of expensive-to-evaluate systems, where the BO algorithm iteratively queries the system and suggests new trials based on a probabilistic model fitted to previous samples. Still, the standard BO loop may require a prohibitively large number of experiments to converge to the optimum, especially for high-dimensional and nonlinear systems. We present a hybrid model-based BO formulation that combines the iterative Bayesian learning of BO with partially known mechanistic physical models. Instead of learning a direct mapping from inputs to the objective, we write all known equations for a physics-based model and infer expressions for variables missing equations using a probabilistic model, in our case, a Gaussian process (GP). The final formulation then includes the GP as a constraint in the hybrid model, thereby allowing other physics-based nonlinear and implicit model constraints. This hybrid model formulation yields a constrained, nonlinear stochastic program, which we discretize using the sample-average approximation. In an in-silico optimization of a single-stage distillation, the hybrid BO model based on mass conservation laws yields significantly better designs than a standard BO loop. Furthermore, the hybrid model converges in as few as one iteration, depending on the initial samples, whereas, the standard BO does not converge within 25 for any of the seeds. Overall, the proposed hybrid BO scheme presents a promising optimization method for partially known systems, leveraging the strengths of both mechanistic modeling and data-driven optimization.

Generative Multi-Objective Bayesian Optimization with Scalable Batch Evaluations for Sample-Efficient De Novo Molecular Design

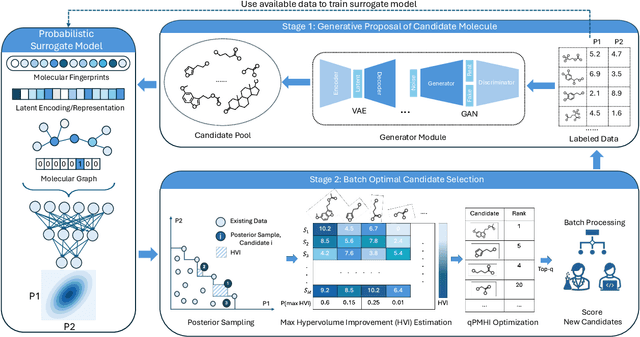
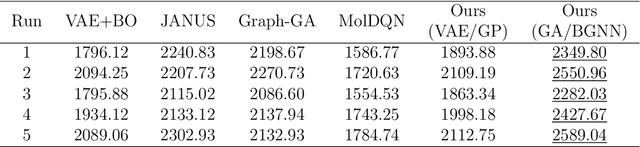
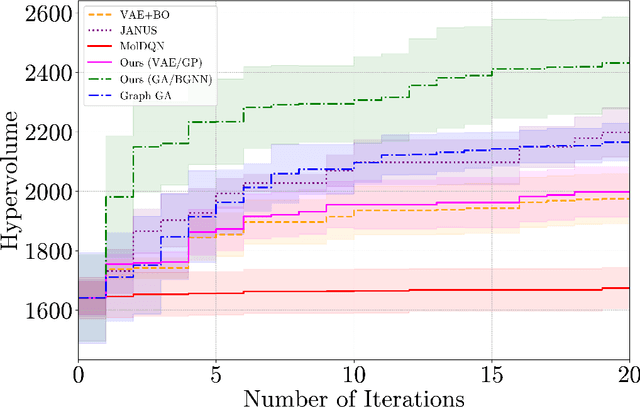
Designing molecules that must satisfy multiple, often conflicting objectives is a central challenge in molecular discovery. The enormous size of chemical space and the cost of high-fidelity simulations have driven the development of machine learning-guided strategies for accelerating design with limited data. Among these, Bayesian optimization (BO) offers a principled framework for sample-efficient search, while generative models provide a mechanism to propose novel, diverse candidates beyond fixed libraries. However, existing methods that couple the two often rely on continuous latent spaces, which introduces both architectural entanglement and scalability challenges. This work introduces an alternative, modular "generate-then-optimize" framework for de novo multi-objective molecular design/discovery. At each iteration, a generative model is used to construct a large, diverse pool of candidate molecules, after which a novel acquisition function, qPMHI (multi-point Probability of Maximum Hypervolume Improvement), is used to optimally select a batch of candidates most likely to induce the largest Pareto front expansion. The key insight is that qPMHI decomposes additively, enabling exact, scalable batch selection via only simple ranking of probabilities that can be easily estimated with Monte Carlo sampling. We benchmark the framework against state-of-the-art latent-space and discrete molecular optimization methods, demonstrating significant improvements across synthetic benchmarks and application-driven tasks. Specifically, in a case study related to sustainable energy storage, we show that our approach quickly uncovers novel, diverse, and high-performing organic (quinone-based) cathode materials for aqueous redox flow battery applications.

Multi-Objective Bayesian Optimization for Networked Black-Box Systems: A Path to Greener Profits and Smarter Designs

Designing modern industrial systems requires balancing several competing objectives, such as profitability, resilience, and sustainability, while accounting for complex interactions between technological, economic, and environmental factors. Multi-objective optimization (MOO) methods are commonly used to navigate these tradeoffs, but selecting the appropriate algorithm to tackle these problems is often unclear, particularly when system representations vary from fully equation-based (white-box) to entirely data-driven (black-box) models. While grey-box MOO methods attempt to bridge this gap, they typically impose rigid assumptions on system structure, requiring models to conform to the underlying structural assumptions of the solver rather than the solver adapting to the natural representation of the system of interest. In this chapter, we introduce a unifying approach to grey-box MOO by leveraging network representations, which provide a general and flexible framework for modeling interconnected systems as a series of function nodes that share various inputs and outputs. Specifically, we propose MOBONS, a novel Bayesian optimization-inspired algorithm that can efficiently optimize general function networks, including those with cyclic dependencies, enabling the modeling of feedback loops, recycle streams, and multi-scale simulations - features that existing methods fail to capture. Furthermore, MOBONS incorporates constraints, supports parallel evaluations, and preserves the sample efficiency of Bayesian optimization while leveraging network structure for improved scalability. We demonstrate the effectiveness of MOBONS through two case studies, including one related to sustainable process design. By enabling efficient MOO under general graph representations, MOBONS has the potential to significantly enhance the design of more profitable, resilient, and sustainable engineering systems.

SyMANTIC: An Efficient Symbolic Regression Method for Interpretable and Parsimonious Model Discovery in Science and Beyond

Symbolic regression (SR) is an emerging branch of machine learning focused on discovering simple and interpretable mathematical expressions from data. Although a wide-variety of SR methods have been developed, they often face challenges such as high computational cost, poor scalability with respect to the number of input dimensions, fragility to noise, and an inability to balance accuracy and complexity. This work introduces SyMANTIC, a novel SR algorithm that addresses these challenges. SyMANTIC efficiently identifies (potentially several) low-dimensional descriptors from a large set of candidates (from $\sim 10^5$ to $\sim 10^{10}$ or more) through a unique combination of mutual information-based feature selection, adaptive feature expansion, and recursively applied $\ell_0$-based sparse regression. In addition, it employs an information-theoretic measure to produce an approximate set of Pareto-optimal equations, each offering the best-found accuracy for a given complexity. Furthermore, our open-source implementation of SyMANTIC, built on the PyTorch ecosystem, facilitates easy installation and GPU acceleration. We demonstrate the effectiveness of SyMANTIC across a range of problems, including synthetic examples, scientific benchmarks, real-world material property predictions, and chaotic dynamical system identification from small datasets. Extensive comparisons show that SyMANTIC uncovers similar or more accurate models at a fraction of the cost of existing SR methods.

TorchSISSO: A PyTorch-Based Implementation of the Sure Independence Screening and Sparsifying Operator for Efficient and Interpretable Model Discovery

Symbolic regression (SR) is a powerful machine learning approach that searches for both the structure and parameters of algebraic models, offering interpretable and compact representations of complex data. Unlike traditional regression methods, SR explores progressively complex feature spaces, which can uncover simple models that generalize well, even from small datasets. Among SR algorithms, the Sure Independence Screening and Sparsifying Operator (SISSO) has proven particularly effective in the natural sciences, helping to rediscover fundamental physical laws as well as discover new interpretable equations for materials property modeling. However, its widespread adoption has been limited by performance inefficiencies and the challenges posed by its FORTRAN-based implementation, especially in modern computing environments. In this work, we introduce TorchSISSO, a native Python implementation built in the PyTorch framework. TorchSISSO leverages GPU acceleration, easy integration, and extensibility, offering a significant speed-up and improved accuracy over the original. We demonstrate that TorchSISSO matches or exceeds the performance of the original SISSO across a range of tasks, while dramatically reducing computational time and improving accessibility for broader scientific applications.

BEACON: A Bayesian Optimization Strategy for Novelty Search in Expensive Black-Box Systems

Novelty search (NS) refers to a class of exploration algorithms that automatically uncover diverse system behaviors through simulations or experiments. Systematically obtaining diverse outcomes is a key component in many real-world design problems such as material and drug discovery, neural architecture search, reinforcement learning, and robot navigation. Since the relationship between the inputs and outputs (i.e., behaviors) of these complex systems is typically not available in closed form, NS requires a black-box perspective. Consequently, popular NS algorithms rely on evolutionary optimization and other meta-heuristics that require intensive sampling of the input space, which is impractical when the system is expensive to evaluate. We propose a Bayesian optimization inspired algorithm for sample-efficient NS that is specifically designed for such expensive black-box systems. Our approach models the input-to-behavior mapping with multi-output Gaussian processes (MOGP) and selects the next point to evaluate by maximizing a novelty metric that depends on a posterior sample drawn from the MOGP that promotes both exploration and exploitation. By leveraging advances in efficient posterior sampling and high-dimensional Gaussian process modeling, we discuss how our approach can be made scalable with respect to both amount of data and number of inputs. We test our approach on ten synthetic benchmark problems and eight real-world problems (with up to 2133 inputs) including new applications such as discovery of diverse metal organic frameworks for use in clean energy technology. We show that our approach greatly outperforms existing NS algorithms by finding substantially larger sets of diverse behaviors under limited sample budgets.

BO4IO: A Bayesian optimization approach to inverse optimization with uncertainty quantification

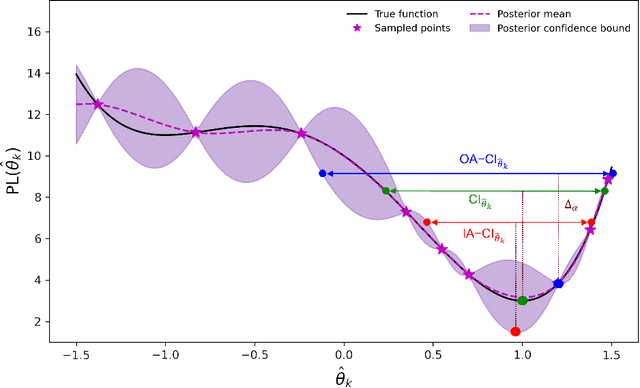
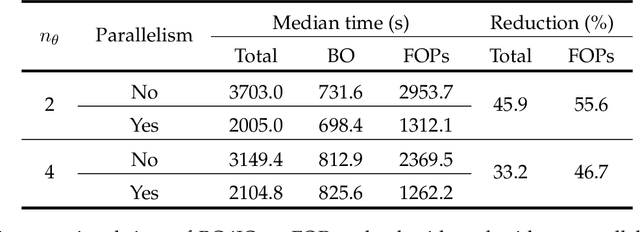
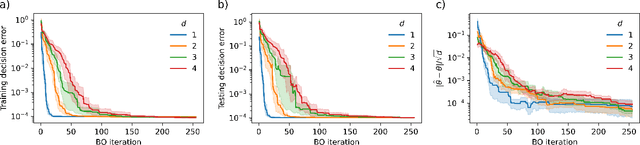
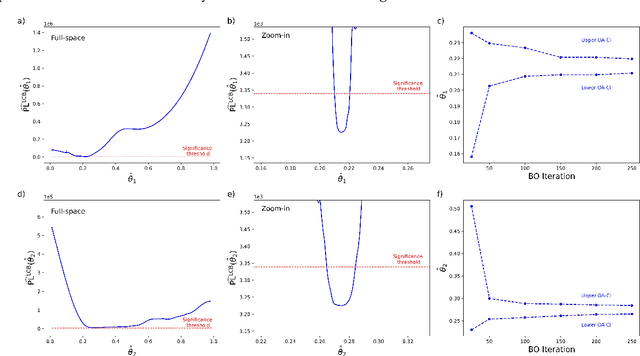
This work addresses data-driven inverse optimization (IO), where the goal is to estimate unknown parameters in an optimization model from observed decisions that can be assumed to be optimal or near-optimal solutions to the optimization problem. The IO problem is commonly formulated as a large-scale bilevel program that is notoriously difficult to solve. Deviating from traditional exact solution methods, we propose a derivative-free optimization approach based on Bayesian optimization, which we call BO4IO, to solve general IO problems. We treat the IO loss function as a black box and approximate it with a Gaussian process model. Using the predicted posterior function, an acquisition function is minimized at each iteration to query new candidate solutions and sequentially converge to the optimal parameter estimates. The main advantages of using Bayesian optimization for IO are two-fold: (i) it circumvents the need of complex reformulations of the bilevel program or specialized algorithms and can hence enable computational tractability even when the underlying optimization problem is nonconvex or involves discrete variables, and (ii) it allows approximations of the profile likelihood, which provide uncertainty quantification on the IO parameter estimates. We apply the proposed method to three computational case studies, covering different classes of forward optimization problems ranging from convex nonlinear to nonconvex mixed-integer nonlinear programs. Our extensive computational results demonstrate the efficacy and robustness of BO4IO to accurately estimate unknown model parameters from small and noisy datasets. In addition, the proposed profile likelihood analysis has proven to be effective in providing good approximations of the confidence intervals on the parameter estimates and assessing the identifiability of the unknown parameters.

CAGES: Cost-Aware Gradient Entropy Search for Efficient Local Multi-Fidelity Bayesian Optimization

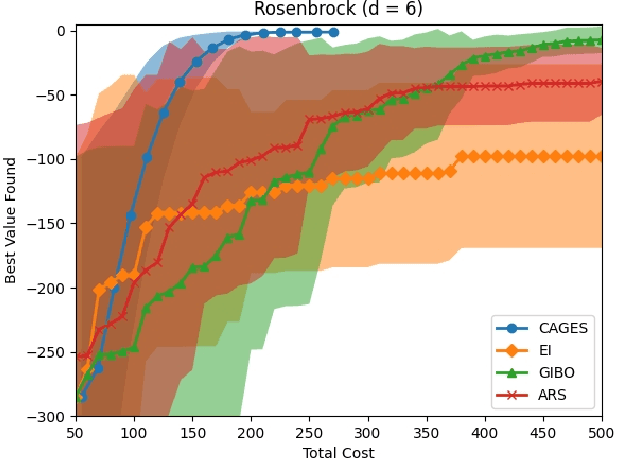
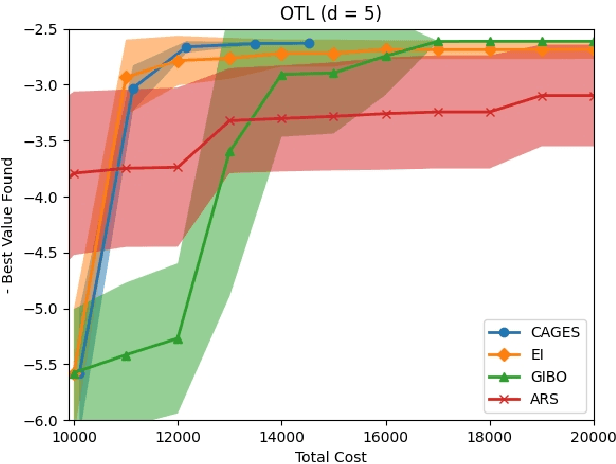
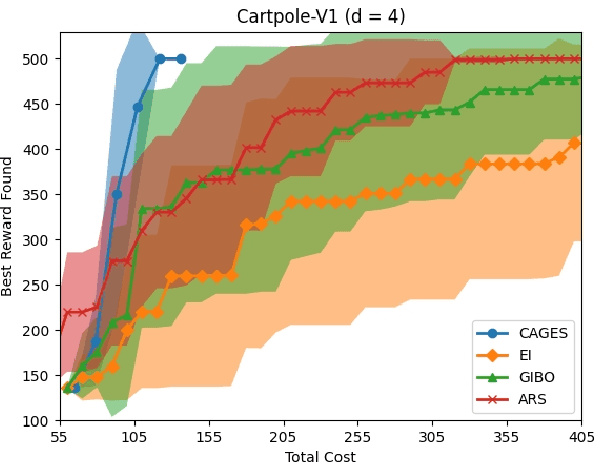
Bayesian optimization (BO) is a popular approach for optimizing expensive-to-evaluate black-box objective functions. An important challenge in BO is its application to high-dimensional search spaces due in large part to the curse of dimensionality. One way to overcome this challenge is to focus on local BO methods that aim to efficiently learn gradients, which have shown strong empirical performance on a variety of high-dimensional problems including policy search in reinforcement learning (RL). However, current local BO methods assume access to only a single high-fidelity information source whereas, in many engineering and control problems, one has access to multiple cheaper approximations of the objective. We propose a novel algorithm, Cost-Aware Gradient Entropy Search (CAGES), for local BO of multi-fidelity black-box functions. CAGES makes no assumption about the relationship between different information sources, making it more flexible than other multi-fidelity methods. It also employs a new type of information-theoretic acquisition function, which enables systematic identification of samples that maximize the information gain about the unknown gradient per cost of the evaluation. We demonstrate CAGES can achieve significant performance improvements compared to other state-of-the-art methods on a variety of synthetic and benchmark RL problems.

Bayesian optimization as a flexible and efficient design framework for sustainable process systems

Bayesian optimization (BO) is a powerful technology for optimizing noisy expensive-to-evaluate black-box functions, with a broad range of real-world applications in science, engineering, economics, manufacturing, and beyond. In this paper, we provide an overview of recent developments, challenges, and opportunities in BO for design of next-generation process systems. After describing several motivating applications, we discuss how advanced BO methods have been developed to more efficiently tackle important problems in these applications. We conclude the paper with a summary of challenges and opportunities related to improving the quality of the probabilistic model, the choice of internal optimization procedure used to select the next sample point, and the exploitation of problem structure to improve sample efficiency.

Accelerating Black-Box Molecular Property Optimization by Adaptively Learning Sparse Subspaces

Molecular property optimization (MPO) problems are inherently challenging since they are formulated over discrete, unstructured spaces and the labeling process involves expensive simulations or experiments, which fundamentally limits the amount of available data. Bayesian optimization (BO) is a powerful and popular framework for efficient optimization of noisy, black-box objective functions (e.g., measured property values), thus is a potentially attractive framework for MPO. To apply BO to MPO problems, one must select a structured molecular representation that enables construction of a probabilistic surrogate model. Many molecular representations have been developed, however, they are all high-dimensional, which introduces important challenges in the BO process -- mainly because the curse of dimensionality makes it difficult to define and perform inference over a suitable class of surrogate models. This challenge has been recently addressed by learning a lower-dimensional encoding of a SMILE or graph representation of a molecule in an unsupervised manner and then performing BO in the encoded space. In this work, we show that such methods have a tendency to "get stuck," which we hypothesize occurs since the mapping from the encoded space to property values is not necessarily well-modeled by a Gaussian process. We argue for an alternative approach that combines numerical molecular descriptors with a sparse axis-aligned Gaussian process model, which is capable of rapidly identifying sparse subspaces that are most relevant to modeling the unknown property function. We demonstrate that our proposed method substantially outperforms existing MPO methods on a variety of benchmark and real-world problems. Specifically, we show that our method can routinely find near-optimal molecules out of a set of more than $>100$k alternatives within 100 or fewer expensive queries.