CAGES: Cost-Aware Gradient Entropy Search for Efficient Local Multi-Fidelity Bayesian Optimization
Paper and Code
May 13, 2024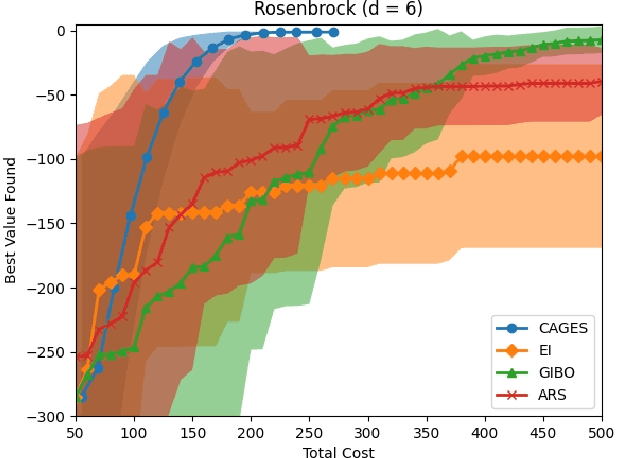
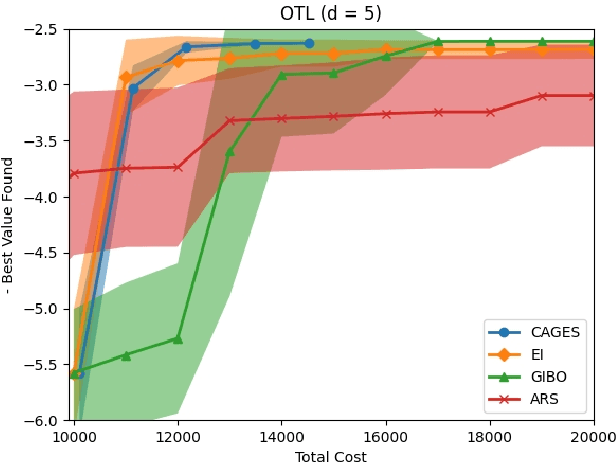
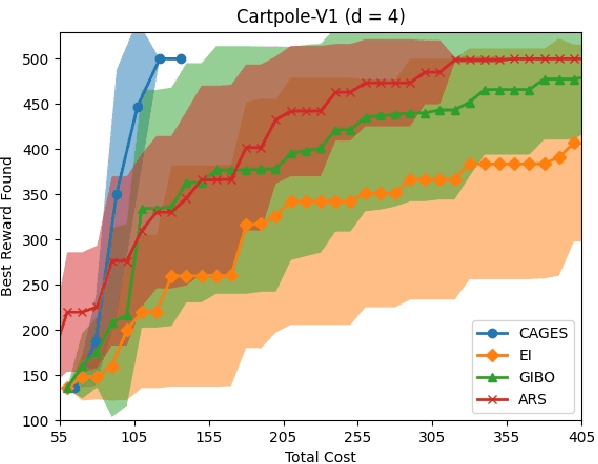
Bayesian optimization (BO) is a popular approach for optimizing expensive-to-evaluate black-box objective functions. An important challenge in BO is its application to high-dimensional search spaces due in large part to the curse of dimensionality. One way to overcome this challenge is to focus on local BO methods that aim to efficiently learn gradients, which have shown strong empirical performance on a variety of high-dimensional problems including policy search in reinforcement learning (RL). However, current local BO methods assume access to only a single high-fidelity information source whereas, in many engineering and control problems, one has access to multiple cheaper approximations of the objective. We propose a novel algorithm, Cost-Aware Gradient Entropy Search (CAGES), for local BO of multi-fidelity black-box functions. CAGES makes no assumption about the relationship between different information sources, making it more flexible than other multi-fidelity methods. It also employs a new type of information-theoretic acquisition function, which enables systematic identification of samples that maximize the information gain about the unknown gradient per cost of the evaluation. We demonstrate CAGES can achieve significant performance improvements compared to other state-of-the-art methods on a variety of synthetic and benchmark RL problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge