Multi-Objective Bayesian Optimization for Networked Black-Box Systems: A Path to Greener Profits and Smarter Designs

Designing modern industrial systems requires balancing several competing objectives, such as profitability, resilience, and sustainability, while accounting for complex interactions between technological, economic, and environmental factors. Multi-objective optimization (MOO) methods are commonly used to navigate these tradeoffs, but selecting the appropriate algorithm to tackle these problems is often unclear, particularly when system representations vary from fully equation-based (white-box) to entirely data-driven (black-box) models. While grey-box MOO methods attempt to bridge this gap, they typically impose rigid assumptions on system structure, requiring models to conform to the underlying structural assumptions of the solver rather than the solver adapting to the natural representation of the system of interest. In this chapter, we introduce a unifying approach to grey-box MOO by leveraging network representations, which provide a general and flexible framework for modeling interconnected systems as a series of function nodes that share various inputs and outputs. Specifically, we propose MOBONS, a novel Bayesian optimization-inspired algorithm that can efficiently optimize general function networks, including those with cyclic dependencies, enabling the modeling of feedback loops, recycle streams, and multi-scale simulations - features that existing methods fail to capture. Furthermore, MOBONS incorporates constraints, supports parallel evaluations, and preserves the sample efficiency of Bayesian optimization while leveraging network structure for improved scalability. We demonstrate the effectiveness of MOBONS through two case studies, including one related to sustainable process design. By enabling efficient MOO under general graph representations, MOBONS has the potential to significantly enhance the design of more profitable, resilient, and sustainable engineering systems.

BEACON: A Bayesian Optimization Strategy for Novelty Search in Expensive Black-Box Systems

Novelty search (NS) refers to a class of exploration algorithms that automatically uncover diverse system behaviors through simulations or experiments. Systematically obtaining diverse outcomes is a key component in many real-world design problems such as material and drug discovery, neural architecture search, reinforcement learning, and robot navigation. Since the relationship between the inputs and outputs (i.e., behaviors) of these complex systems is typically not available in closed form, NS requires a black-box perspective. Consequently, popular NS algorithms rely on evolutionary optimization and other meta-heuristics that require intensive sampling of the input space, which is impractical when the system is expensive to evaluate. We propose a Bayesian optimization inspired algorithm for sample-efficient NS that is specifically designed for such expensive black-box systems. Our approach models the input-to-behavior mapping with multi-output Gaussian processes (MOGP) and selects the next point to evaluate by maximizing a novelty metric that depends on a posterior sample drawn from the MOGP that promotes both exploration and exploitation. By leveraging advances in efficient posterior sampling and high-dimensional Gaussian process modeling, we discuss how our approach can be made scalable with respect to both amount of data and number of inputs. We test our approach on ten synthetic benchmark problems and eight real-world problems (with up to 2133 inputs) including new applications such as discovery of diverse metal organic frameworks for use in clean energy technology. We show that our approach greatly outperforms existing NS algorithms by finding substantially larger sets of diverse behaviors under limited sample budgets.

CAGES: Cost-Aware Gradient Entropy Search for Efficient Local Multi-Fidelity Bayesian Optimization

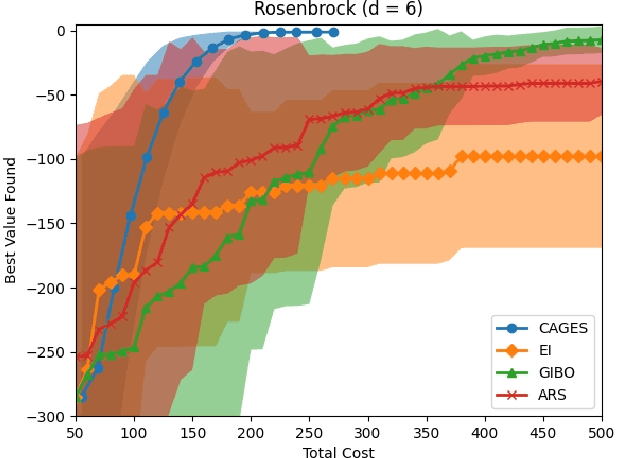
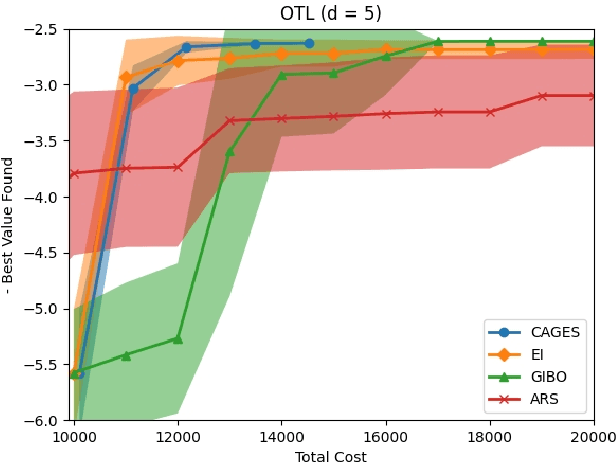
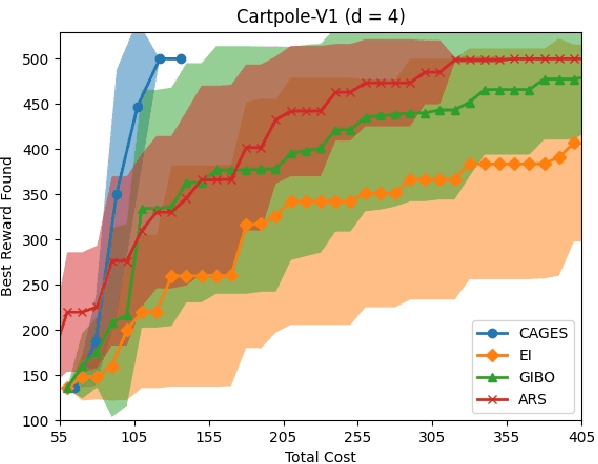
Bayesian optimization (BO) is a popular approach for optimizing expensive-to-evaluate black-box objective functions. An important challenge in BO is its application to high-dimensional search spaces due in large part to the curse of dimensionality. One way to overcome this challenge is to focus on local BO methods that aim to efficiently learn gradients, which have shown strong empirical performance on a variety of high-dimensional problems including policy search in reinforcement learning (RL). However, current local BO methods assume access to only a single high-fidelity information source whereas, in many engineering and control problems, one has access to multiple cheaper approximations of the objective. We propose a novel algorithm, Cost-Aware Gradient Entropy Search (CAGES), for local BO of multi-fidelity black-box functions. CAGES makes no assumption about the relationship between different information sources, making it more flexible than other multi-fidelity methods. It also employs a new type of information-theoretic acquisition function, which enables systematic identification of samples that maximize the information gain about the unknown gradient per cost of the evaluation. We demonstrate CAGES can achieve significant performance improvements compared to other state-of-the-art methods on a variety of synthetic and benchmark RL problems.