BO4IO: A Bayesian optimization approach to inverse optimization with uncertainty quantification
Paper and Code
May 28, 2024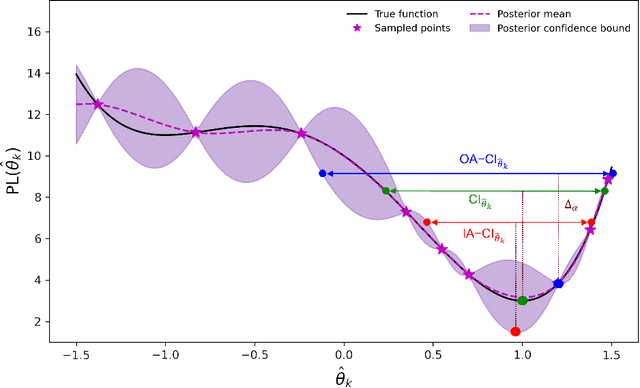
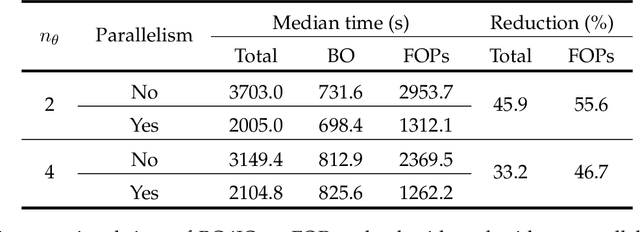
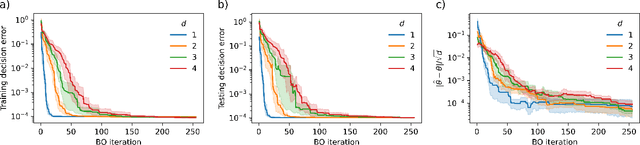
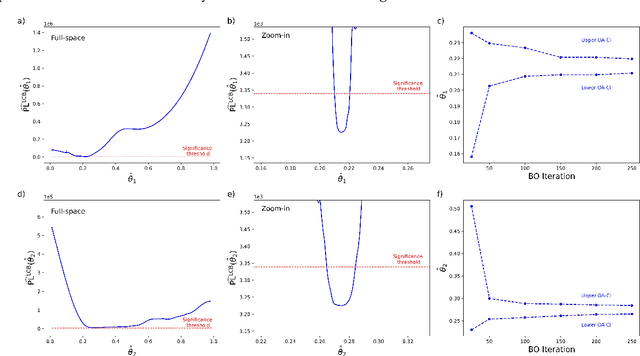
This work addresses data-driven inverse optimization (IO), where the goal is to estimate unknown parameters in an optimization model from observed decisions that can be assumed to be optimal or near-optimal solutions to the optimization problem. The IO problem is commonly formulated as a large-scale bilevel program that is notoriously difficult to solve. Deviating from traditional exact solution methods, we propose a derivative-free optimization approach based on Bayesian optimization, which we call BO4IO, to solve general IO problems. We treat the IO loss function as a black box and approximate it with a Gaussian process model. Using the predicted posterior function, an acquisition function is minimized at each iteration to query new candidate solutions and sequentially converge to the optimal parameter estimates. The main advantages of using Bayesian optimization for IO are two-fold: (i) it circumvents the need of complex reformulations of the bilevel program or specialized algorithms and can hence enable computational tractability even when the underlying optimization problem is nonconvex or involves discrete variables, and (ii) it allows approximations of the profile likelihood, which provide uncertainty quantification on the IO parameter estimates. We apply the proposed method to three computational case studies, covering different classes of forward optimization problems ranging from convex nonlinear to nonconvex mixed-integer nonlinear programs. Our extensive computational results demonstrate the efficacy and robustness of BO4IO to accurately estimate unknown model parameters from small and noisy datasets. In addition, the proposed profile likelihood analysis has proven to be effective in providing good approximations of the confidence intervals on the parameter estimates and assessing the identifiability of the unknown parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge