The Catechol Benchmark: Time-series Solvent Selection Data for Few-shot Machine Learning

Machine learning has promised to change the landscape of laboratory chemistry, with impressive results in molecular property prediction and reaction retro-synthesis. However, chemical datasets are often inaccessible to the machine learning community as they tend to require cleaning, thorough understanding of the chemistry, or are simply not available. In this paper, we introduce a novel dataset for yield prediction, providing the first-ever transient flow dataset for machine learning benchmarking, covering over 1200 process conditions. While previous datasets focus on discrete parameters, our experimental set-up allow us to sample a large number of continuous process conditions, generating new challenges for machine learning models. We focus on solvent selection, a task that is particularly difficult to model theoretically and therefore ripe for machine learning applications. We showcase benchmarking for regression algorithms, transfer-learning approaches, feature engineering, and active learning, with important applications towards solvent replacement and sustainable manufacturing.

Global optimization of graph acquisition functions for neural architecture search

Graph Bayesian optimization (BO) has shown potential as a powerful and data-efficient tool for neural architecture search (NAS). Most existing graph BO works focus on developing graph surrogates models, i.e., metrics of networks and/or different kernels to quantify the similarity between networks. However, the acquisition optimization, as a discrete optimization task over graph structures, is not well studied due to the complexity of formulating the graph search space and acquisition functions. This paper presents explicit optimization formulations for graph input space including properties such as reachability and shortest paths, which are used later to formulate graph kernels and the acquisition function. We theoretically prove that the proposed encoding is an equivalent representation of the graph space and provide restrictions for the NAS domain with either node or edge labels. Numerical results over several NAS benchmarks show that our method efficiently finds the optimal architecture for most cases, highlighting its efficacy.

Training Neural ODEs Using Fully Discretized Simultaneous Optimization

Neural Ordinary Differential Equations (Neural ODEs) represent continuous-time dynamics with neural networks, offering advancements for modeling and control tasks. However, training Neural ODEs requires solving differential equations at each epoch, leading to high computational costs. This work investigates simultaneous optimization methods as a faster training alternative. In particular, we employ a collocation-based, fully discretized formulation and use IPOPT--a solver for large-scale nonlinear optimization--to simultaneously optimize collocation coefficients and neural network parameters. Using the Van der Pol Oscillator as a case study, we demonstrate faster convergence compared to traditional training methods. Furthermore, we introduce a decomposition framework utilizing Alternating Direction Method of Multipliers (ADMM) to effectively coordinate sub-models among data batches. Our results show significant potential for (collocation-based) simultaneous Neural ODE training pipelines.

EARL-BO: Reinforcement Learning for Multi-Step Lookahead, High-Dimensional Bayesian Optimization

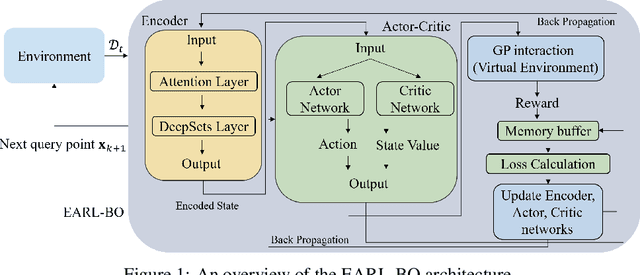
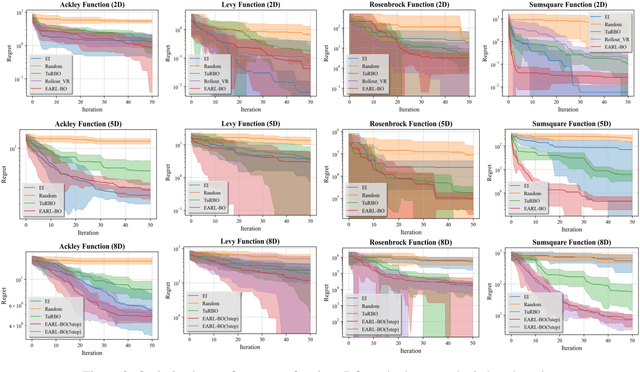
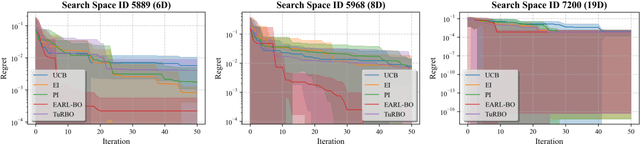
Conventional methods for Bayesian optimization (BO) primarily involve one-step optimal decisions (e.g., maximizing expected improvement of the next step). To avoid myopic behavior, multi-step lookahead BO algorithms such as rollout strategies consider the sequential decision-making nature of BO, i.e., as a stochastic dynamic programming (SDP) problem, demonstrating promising results in recent years. However, owing to the curse of dimensionality, most of these methods make significant approximations or suffer scalability issues, e.g., being limited to two-step lookahead. This paper presents a novel reinforcement learning (RL)-based framework for multi-step lookahead BO in high-dimensional black-box optimization problems. The proposed method enhances the scalability and decision-making quality of multi-step lookahead BO by efficiently solving the SDP of the BO process in a near-optimal manner using RL. We first introduce an Attention-DeepSets encoder to represent the state of knowledge to the RL agent and employ off-policy learning to accelerate its initial training. We then propose a multi-task, fine-tuning procedure based on end-to-end (encoder-RL) on-policy learning. We evaluate the proposed method, EARL-BO (Encoder Augmented RL for Bayesian Optimization), on both synthetic benchmark functions and real-world hyperparameter optimization problems, demonstrating significantly improved performance compared to existing multi-step lookahead and high-dimensional BO methods.

Global Optimization of Gaussian Process Acquisition Functions Using a Piecewise-Linear Kernel Approximation

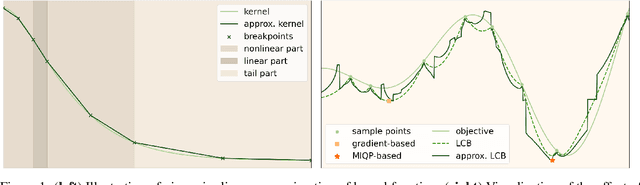
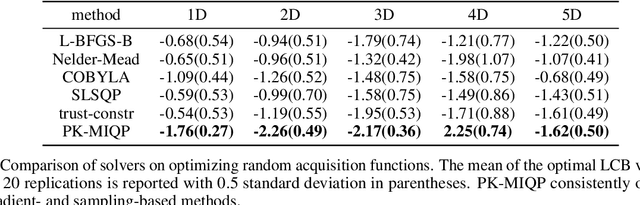
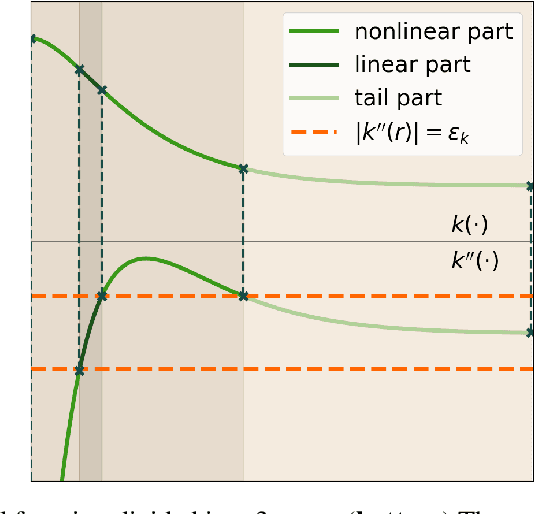
Bayesian optimization relies on iteratively constructing and optimizing an acquisition function. The latter turns out to be a challenging, non-convex optimization problem itself. Despite the relative importance of this step, most algorithms employ sampling- or gradient-based methods, which do not provably converge to global optima. This work investigates mixed-integer programming (MIP) as a paradigm for \textit{global} acquisition function optimization. Specifically, our Piecewise-linear Kernel Mixed Integer Quadratic Programming (PK-MIQP) formulation introduces a piecewise-linear approximation for Gaussian process kernels and admits a corresponding MIQP representation for acquisition functions. We analyze the theoretical regret bounds of the proposed approximation, and empirically demonstrate the framework on synthetic functions, constrained benchmarks, and a hyperparameter tuning task.

Certificates of Differential Privacy and Unlearning for Gradient-Based Training

Proper data stewardship requires that model owners protect the privacy of individuals' data used during training. Whether through anonymization with differential privacy or the use of unlearning in non-anonymized settings, the gold-standard techniques for providing privacy guarantees can come with significant performance penalties or be too weak to provide practical assurances. In part, this is due to the fact that the guarantee provided by differential privacy represents the worst-case privacy leakage for any individual, while the true privacy leakage of releasing the prediction for a given individual might be substantially smaller or even, as we show, non-existent. This work provides a novel framework based on convex relaxations and bounds propagation that can compute formal guarantees (certificates) that releasing specific predictions satisfies $\epsilon=0$ privacy guarantees or do not depend on data that is subject to an unlearning request. Our framework offers a new verification-centric approach to privacy and unlearning guarantees, that can be used to further engender user trust with tighter privacy guarantees, provide formal proofs of robustness to certain membership inference attacks, identify potentially vulnerable records, and enhance current unlearning approaches. We validate the effectiveness of our approach on tasks from financial services, medical imaging, and natural language processing.

Certified Robustness to Data Poisoning in Gradient-Based Training

Modern machine learning pipelines leverage large amounts of public data, making it infeasible to guarantee data quality and leaving models open to poisoning and backdoor attacks. However, provably bounding model behavior under such attacks remains an open problem. In this work, we address this challenge and develop the first framework providing provable guarantees on the behavior of models trained with potentially manipulated data. In particular, our framework certifies robustness against untargeted and targeted poisoning as well as backdoor attacks for both input and label manipulations. Our method leverages convex relaxations to over-approximate the set of all possible parameter updates for a given poisoning threat model, allowing us to bound the set of all reachable parameters for any gradient-based learning algorithm. Given this set of parameters, we provide bounds on worst-case behavior, including model performance and backdoor success rate. We demonstrate our approach on multiple real-world datasets from applications including energy consumption, medical imaging, and autonomous driving.

System-Aware Neural ODE Processes for Few-Shot Bayesian Optimization

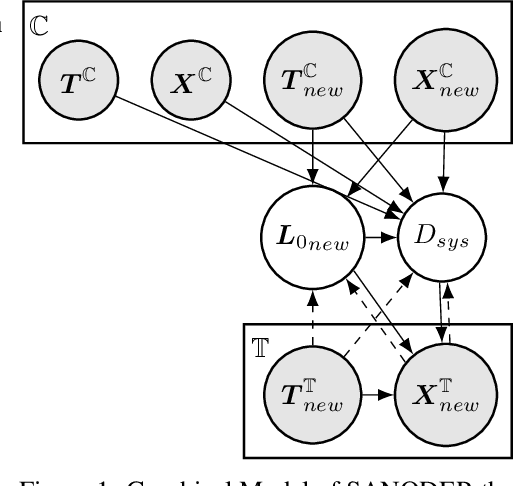
We consider the problem of optimizing initial conditions and timing in dynamical systems governed by unknown ordinary differential equations (ODEs), where evaluating different initial conditions is costly and there are constraints on observation times. To identify the optimal conditions within several trials, we introduce a few-shot Bayesian Optimization (BO) framework based on the system's prior information. At the core of our approach is the System-Aware Neural ODE Processes (SANODEP), an extension of Neural ODE Processes (NODEP) designed to meta-learn ODE systems from multiple trajectories using a novel context embedding block. Additionally, we propose a multi-scenario loss function specifically for optimization purposes. Our two-stage BO framework effectively incorporates search space constraints, enabling efficient optimization of both initial conditions and observation timings. We conduct extensive experiments showcasing SANODEP's potential for few-shot BO. We also explore SANODEP's adaptability to varying levels of prior information, highlighting the trade-off between prior flexibility and model fitting accuracy.

Transition Constrained Bayesian Optimization via Markov Decision Processes

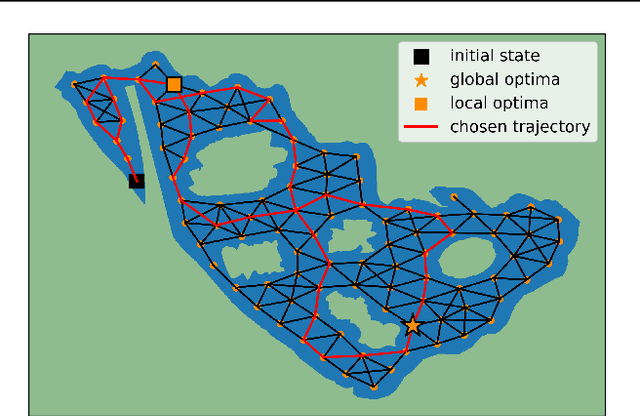
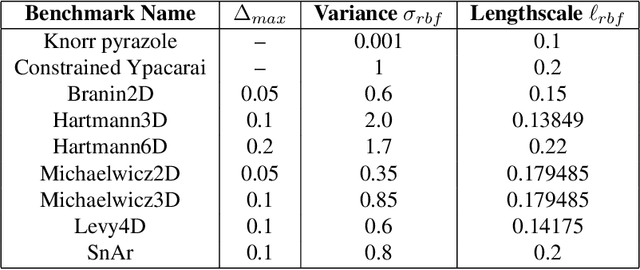
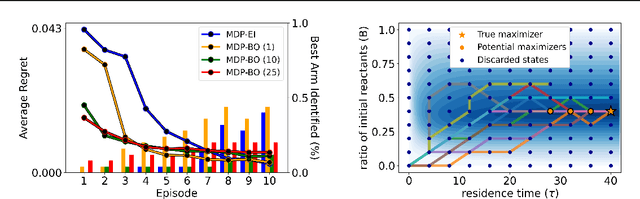
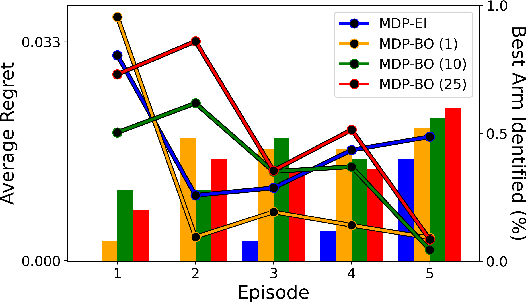
Bayesian optimization is a methodology to optimize black-box functions. Traditionally, it focuses on the setting where you can arbitrarily query the search space. However, many real-life problems do not offer this flexibility; in particular, the search space of the next query may depend on previous ones. Example challenges arise in the physical sciences in the form of local movement constraints, required monotonicity in certain variables, and transitions influencing the accuracy of measurements. Altogether, such transition constraints necessitate a form of planning. This work extends Bayesian optimization via the framework of Markov Decision Processes, iteratively solving a tractable linearization of our objective using reinforcement learning to obtain a policy that plans ahead over long horizons. The resulting policy is potentially history-dependent and non-Markovian. We showcase applications in chemical reactor optimization, informative path planning, machine calibration, and other synthetic examples.

Bayesian optimization as a flexible and efficient design framework for sustainable process systems

Bayesian optimization (BO) is a powerful technology for optimizing noisy expensive-to-evaluate black-box functions, with a broad range of real-world applications in science, engineering, economics, manufacturing, and beyond. In this paper, we provide an overview of recent developments, challenges, and opportunities in BO for design of next-generation process systems. After describing several motivating applications, we discuss how advanced BO methods have been developed to more efficiently tackle important problems in these applications. We conclude the paper with a summary of challenges and opportunities related to improving the quality of the probabilistic model, the choice of internal optimization procedure used to select the next sample point, and the exploitation of problem structure to improve sample efficiency.