Becky D Langdon
System-Aware Neural ODE Processes for Few-Shot Bayesian Optimization
Jun 04, 2024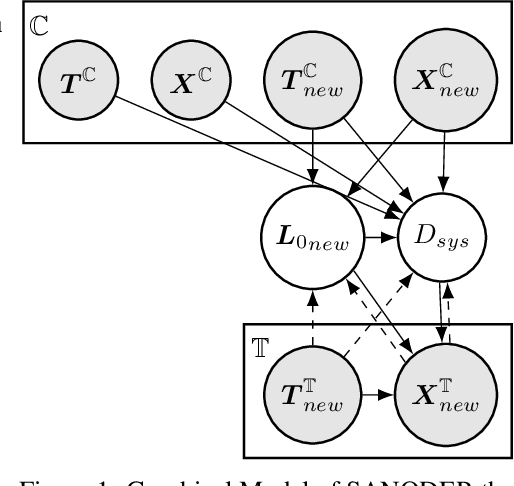



Abstract:We consider the problem of optimizing initial conditions and timing in dynamical systems governed by unknown ordinary differential equations (ODEs), where evaluating different initial conditions is costly and there are constraints on observation times. To identify the optimal conditions within several trials, we introduce a few-shot Bayesian Optimization (BO) framework based on the system's prior information. At the core of our approach is the System-Aware Neural ODE Processes (SANODEP), an extension of Neural ODE Processes (NODEP) designed to meta-learn ODE systems from multiple trajectories using a novel context embedding block. Additionally, we propose a multi-scenario loss function specifically for optimization purposes. Our two-stage BO framework effectively incorporates search space constraints, enabling efficient optimization of both initial conditions and observation timings. We conduct extensive experiments showcasing SANODEP's potential for few-shot BO. We also explore SANODEP's adaptability to varying levels of prior information, highlighting the trade-off between prior flexibility and model fitting accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge