System-Aware Neural ODE Processes for Few-Shot Bayesian Optimization

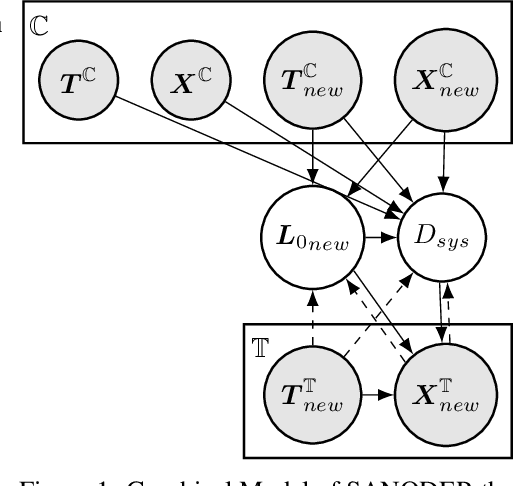
We consider the problem of optimizing initial conditions and timing in dynamical systems governed by unknown ordinary differential equations (ODEs), where evaluating different initial conditions is costly and there are constraints on observation times. To identify the optimal conditions within several trials, we introduce a few-shot Bayesian Optimization (BO) framework based on the system's prior information. At the core of our approach is the System-Aware Neural ODE Processes (SANODEP), an extension of Neural ODE Processes (NODEP) designed to meta-learn ODE systems from multiple trajectories using a novel context embedding block. Additionally, we propose a multi-scenario loss function specifically for optimization purposes. Our two-stage BO framework effectively incorporates search space constraints, enabling efficient optimization of both initial conditions and observation timings. We conduct extensive experiments showcasing SANODEP's potential for few-shot BO. We also explore SANODEP's adaptability to varying levels of prior information, highlighting the trade-off between prior flexibility and model fitting accuracy.

Trieste: Efficiently Exploring The Depths of Black-box Functions with TensorFlow

We present Trieste, an open-source Python package for Bayesian optimization and active learning benefiting from the scalability and efficiency of TensorFlow. Our library enables the plug-and-play of popular TensorFlow-based models within sequential decision-making loops, e.g. Gaussian processes from GPflow or GPflux, or neural networks from Keras. This modular mindset is central to the package and extends to our acquisition functions and the internal dynamics of the decision-making loop, both of which can be tailored and extended by researchers or engineers when tackling custom use cases. Trieste is a research-friendly and production-ready toolkit backed by a comprehensive test suite, extensive documentation, and available at https://github.com/secondmind-labs/trieste.

$\{\text{PF}\}^2\text{ES}$: Parallel Feasible Pareto Frontier Entropy Search for Multi-Objective Bayesian Optimization Under Unknown Constraints

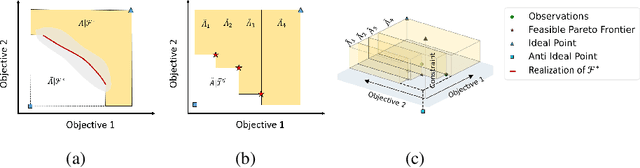
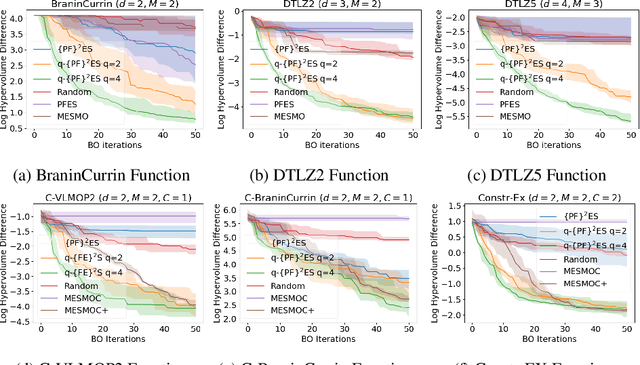
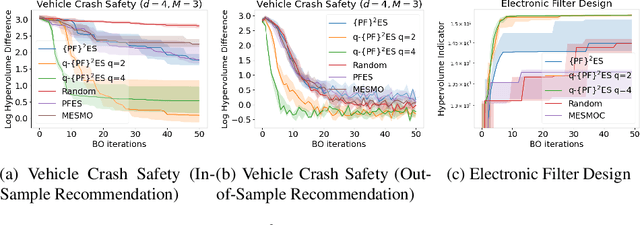
We present Parallel Feasible Pareto Frontier Entropy Search ($\{\text{PF}\}^2$ES) -- a novel information-theoretic acquisition function for multi-objective Bayesian optimization. Although information-theoretic approaches regularly provide state-of-the-art optimization, they are not yet widely used in the context of constrained multi-objective optimization. Due to the complexity of characterizing mutual information between candidate evaluations and (feasible) Pareto frontiers, existing approaches must employ severe approximations that significantly hamper their performance. By instead using a variational lower bound, $\{\text{PF}\}^2$ES provides a low cost and accurate estimate of the mutual information for the parallel setting (where multiple evaluations must be chosen for each optimization step). Moreover, we are able to interpret our proposed acquisition function by exploring direct links with other popular multi-objective acquisition functions. We benchmark $\{\text{PF}\}^2$ES across synthetic and real-life problems, demonstrating its competitive performance for batch optimization across synthetic and real-world problems including vehicle and electronic filter design.