MONGOOSE: Path-wise Smooth Bayesian Optimisation via Meta-learning

In Bayesian optimisation, we often seek to minimise the black-box objective functions that arise in real-world physical systems. A primary contributor to the cost of evaluating such black-box objective functions is often the effort required to prepare the system for measurement. We consider a common scenario where preparation costs grow as the distance between successive evaluations increases. In this setting, smooth optimisation trajectories are preferred and the jumpy paths produced by the standard myopic (i.e.\ one-step-optimal) Bayesian optimisation methods are sub-optimal. Our algorithm, MONGOOSE, uses a meta-learnt parametric policy to generate smooth optimisation trajectories, achieving performance gains over existing methods when optimising functions with large movement costs.

Trieste: Efficiently Exploring The Depths of Black-box Functions with TensorFlow

We present Trieste, an open-source Python package for Bayesian optimization and active learning benefiting from the scalability and efficiency of TensorFlow. Our library enables the plug-and-play of popular TensorFlow-based models within sequential decision-making loops, e.g. Gaussian processes from GPflow or GPflux, or neural networks from Keras. This modular mindset is central to the package and extends to our acquisition functions and the internal dynamics of the decision-making loop, both of which can be tailored and extended by researchers or engineers when tackling custom use cases. Trieste is a research-friendly and production-ready toolkit backed by a comprehensive test suite, extensive documentation, and available at https://github.com/secondmind-labs/trieste.

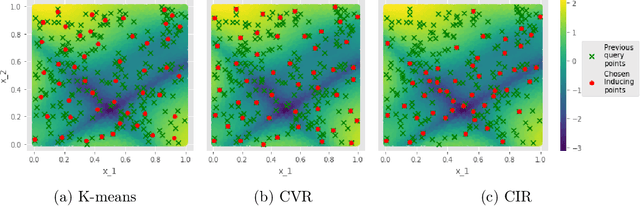
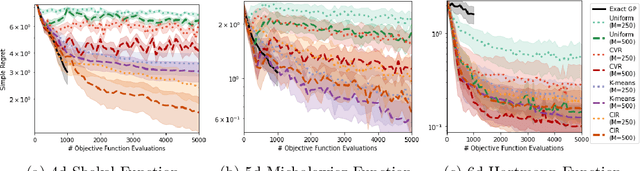
Inducing Point Allocation for Sparse Gaussian Processes in High-Throughput Bayesian Optimisation

Sparse Gaussian Processes are a key component of high-throughput Bayesian Optimisation (BO) loops; however, we show that existing methods for allocating their inducing points severely hamper optimisation performance. By exploiting the quality-diversity decomposition of Determinantal Point Processes, we propose the first inducing point allocation strategy designed specifically for use in BO. Unlike existing methods which seek only to reduce global uncertainty in the objective function, our approach provides the local high-fidelity modelling of promising regions required for precise optimisation. More generally, we demonstrate that our proposed framework provides a flexible way to allocate modelling capacity in sparse models and so is suitable broad range of downstream sequential decision making tasks.

GAUCHE: A Library for Gaussian Processes in Chemistry

We introduce GAUCHE, a library for GAUssian processes in CHEmistry. Gaussian processes have long been a cornerstone of probabilistic machine learning, affording particular advantages for uncertainty quantification and Bayesian optimisation. Extending Gaussian processes to chemical representations, however, is nontrivial, necessitating kernels defined over structured inputs such as graphs, strings and bit vectors. By defining such kernels in GAUCHE, we seek to open the door to powerful tools for uncertainty quantification and Bayesian optimisation in chemistry. Motivated by scenarios frequently encountered in experimental chemistry, we showcase applications for GAUCHE in molecular discovery and chemical reaction optimisation. The codebase is made available at https://github.com/leojklarner/gauche

A penalisation method for batch multi-objective Bayesian optimisation with application in heat exchanger design

We present HIghly Parallelisable Pareto Optimisation (HIPPO) -- a batch acquisition function that enables multi-objective Bayesian optimisation methods to efficiently exploit parallel processing resources. Multi-Objective Bayesian Optimisation (MOBO) is a very efficient tool for tackling expensive black-box problems. However, most MOBO algorithms are designed as purely sequential strategies, and existing batch approaches are prohibitively expensive for all but the smallest of batch sizes. We show that by encouraging batch diversity through penalising evaluations with similar predicted objective values, HIPPO is able to cheaply build large batches of informative points. Our extensive experimental validation demonstrates that HIPPO is at least as efficient as existing alternatives whilst incurring an order of magnitude lower computational overhead and scaling easily to batch sizes considerably higher than currently supported in the literature. Additionally, we demonstrate the application of HIPPO to a challenging heat exchanger design problem, stressing the real-world utility of our highly parallelisable approach to MOBO.

Information-theoretic Inducing Point Placement for High-throughput Bayesian Optimisation

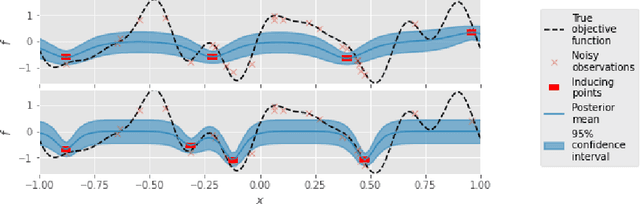
Sparse Gaussian Processes are a key component of high-throughput Bayesian optimisation (BO) loops -- an increasingly common setting where evaluation budgets are large and highly parallelised. By using representative subsets of the available data to build approximate posteriors, sparse models dramatically reduce the computational costs of surrogate modelling by relying on a small set of pseudo-observations, the so-called inducing points, in lieu of the full data set. However, current approaches to design inducing points are not appropriate within BO loops as they seek to reduce global uncertainty in the objective function. Thus, the high-fidelity modelling of promising and data-dense regions required for precise optimisation is sacrificed and computational resources are instead wasted on modelling areas of the space already known to be sub-optimal. Inspired by entropy-based BO methods, we propose a novel inducing point design that uses a principled information-theoretic criterion to select inducing points. By choosing inducing points to maximally reduce both global uncertainty and uncertainty in the maximum value of the objective function, we build surrogate models able to support high-precision high-throughput BO.

$\{\text{PF}\}^2\text{ES}$: Parallel Feasible Pareto Frontier Entropy Search for Multi-Objective Bayesian Optimization Under Unknown Constraints

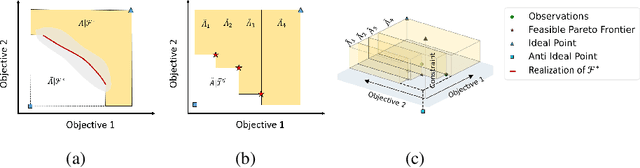
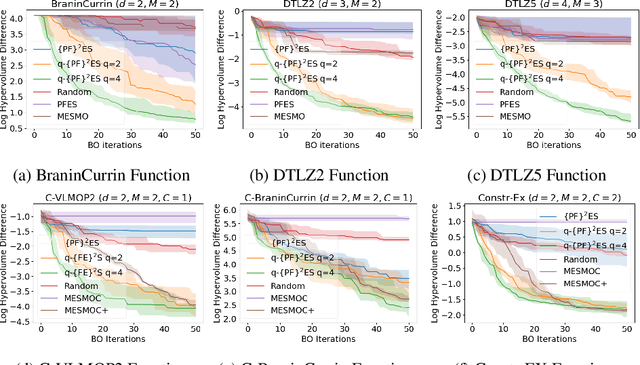
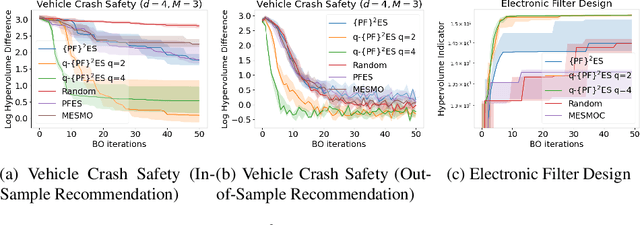
We present Parallel Feasible Pareto Frontier Entropy Search ($\{\text{PF}\}^2$ES) -- a novel information-theoretic acquisition function for multi-objective Bayesian optimization. Although information-theoretic approaches regularly provide state-of-the-art optimization, they are not yet widely used in the context of constrained multi-objective optimization. Due to the complexity of characterizing mutual information between candidate evaluations and (feasible) Pareto frontiers, existing approaches must employ severe approximations that significantly hamper their performance. By instead using a variational lower bound, $\{\text{PF}\}^2$ES provides a low cost and accurate estimate of the mutual information for the parallel setting (where multiple evaluations must be chosen for each optimization step). Moreover, we are able to interpret our proposed acquisition function by exploring direct links with other popular multi-objective acquisition functions. We benchmark $\{\text{PF}\}^2$ES across synthetic and real-life problems, demonstrating its competitive performance for batch optimization across synthetic and real-world problems including vehicle and electronic filter design.

GIBBON: General-purpose Information-Based Bayesian OptimisatioN

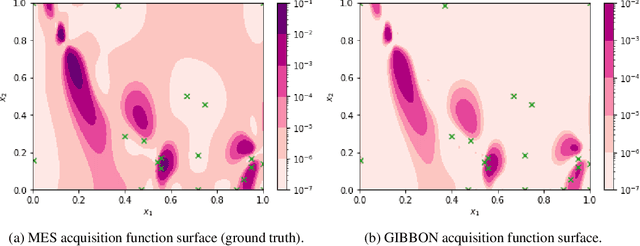
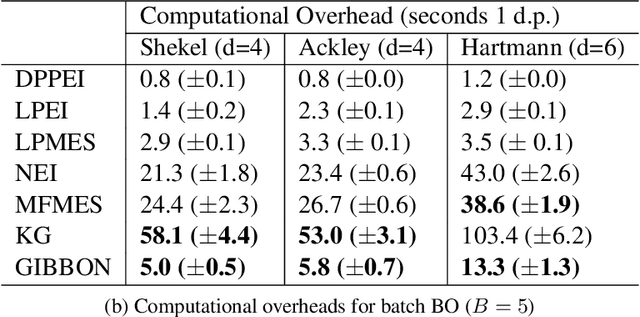
This paper describes a general-purpose extension of max-value entropy search, a popular approach for Bayesian Optimisation (BO). A novel approximation is proposed for the information gain -- an information-theoretic quantity central to solving a range of BO problems, including noisy, multi-fidelity and batch optimisations across both continuous and highly-structured discrete spaces. Previously, these problems have been tackled separately within information-theoretic BO, each requiring a different sophisticated approximation scheme, except for batch BO, for which no computationally-lightweight information-theoretic approach has previously been proposed. GIBBON (General-purpose Information-Based Bayesian OptimisatioN) provides a single principled framework suitable for all the above, out-performing existing approaches whilst incurring substantially lower computational overheads. In addition, GIBBON does not require the problem's search space to be Euclidean and so is the first high-performance yet computationally light-weight acquisition function that supports batch BO over general highly structured input spaces like molecular search and gene design. Moreover, our principled derivation of GIBBON yields a natural interpretation of a popular batch BO heuristic based on determinantal point processes. Finally, we analyse GIBBON across a suite of synthetic benchmark tasks, a molecular search loop, and as part of a challenging batch multi-fidelity framework for problems with controllable experimental noise.

Gaussian Process Molecule Property Prediction with FlowMO

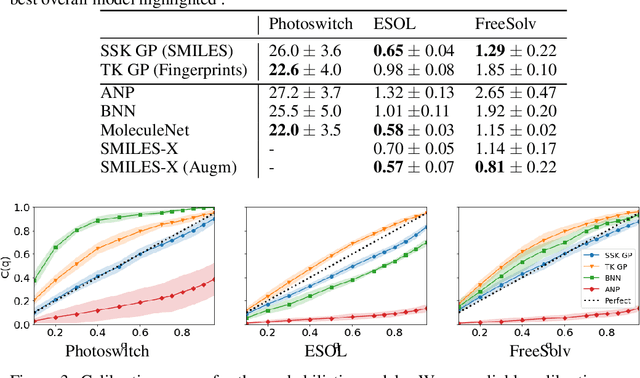
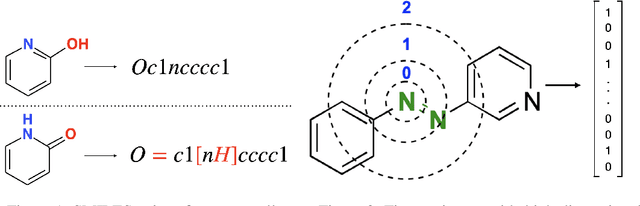
We present FlowMO: an open-source Python library for molecular property prediction with Gaussian Processes. Built upon GPflow and RDKit, FlowMO enables the user to make predictions with well-calibrated uncertainty estimates, an output central to active learning and molecular design applications. Gaussian Processes are particularly attractive for modelling small molecular datasets, a characteristic of many real-world virtual screening campaigns where high-quality experimental data is scarce. Computational experiments across three small datasets demonstrate comparable predictive performance to deep learning methods but with superior uncertainty calibration.