Aviary: training language agents on challenging scientific tasks

Solving complex real-world tasks requires cycles of actions and observations. This is particularly true in science, where tasks require many cycles of analysis, tool use, and experimentation. Language agents are promising for automating intellectual tasks in science because they can interact with tools via natural language or code. Yet their flexibility creates conceptual and practical challenges for software implementations, since agents may comprise non-standard components such as internal reasoning, planning, tool usage, as well as the inherent stochasticity of temperature-sampled language models. Here, we introduce Aviary, an extensible gymnasium for language agents. We formalize agents as policies solving language-grounded partially observable Markov decision processes, which we term language decision processes. We then implement five environments, including three challenging scientific environments: (1) manipulating DNA constructs for molecular cloning, (2) answering research questions by accessing scientific literature, and (3) engineering protein stability. These environments were selected for their focus on multi-step reasoning and their relevance to contemporary biology research. Finally, with online training and scaling inference-time compute, we show that language agents backed by open-source, non-frontier LLMs can match and exceed both frontier LLM agents and human experts on multiple tasks at up to 100x lower inference cost.

Data for Mathematical Copilots: Better Ways of Presenting Proofs for Machine Learning

The suite of datasets commonly used to train and evaluate the mathematical capabilities of AI-based mathematical copilots (primarily large language models) exhibit several shortcomings. These limitations include a restricted scope of mathematical complexity, typically not exceeding lower undergraduate-level mathematics, binary rating protocols and other issues, which makes comprehensive proof-based evaluation suites difficult. We systematically explore these limitations and contend that enhancing the capabilities of large language models, or any forthcoming advancements in AI-based mathematical assistants (copilots or "thought partners"), necessitates a paradigm shift in the design of mathematical datasets and the evaluation criteria of mathematical ability: It is necessary to move away from result-based datasets (theorem statement to theorem proof) and convert the rich facets of mathematical research practice to data LLMs can train on. Examples of these are mathematical workflows (sequences of atomic, potentially subfield-dependent tasks that are often performed when creating new mathematics), which are an important part of the proof-discovery process. Additionally, we advocate for mathematical dataset developers to consider the concept of "motivated proof", introduced by G. P\'olya in 1949, which can serve as a blueprint for datasets that offer a better proof learning signal, alleviating some of the mentioned limitations. Lastly, we introduce math datasheets for datasets, extending the general, dataset-agnostic variants of datasheets: We provide a questionnaire designed specifically for math datasets that we urge dataset creators to include with their datasets. This will make creators aware of potential limitations of their datasets while at the same time making it easy for readers to assess it from the point of view of training and evaluating mathematical copilots.

RealMedQA: A pilot biomedical question answering dataset containing realistic clinical questions

Clinical question answering systems have the potential to provide clinicians with relevant and timely answers to their questions. Nonetheless, despite the advances that have been made, adoption of these systems in clinical settings has been slow. One issue is a lack of question-answering datasets which reflect the real-world needs of health professionals. In this work, we present RealMedQA, a dataset of realistic clinical questions generated by humans and an LLM. We describe the process for generating and verifying the QA pairs and assess several QA models on BioASQ and RealMedQA to assess the relative difficulty of matching answers to questions. We show that the LLM is more cost-efficient for generating "ideal" QA pairs. Additionally, we achieve a lower lexical similarity between questions and answers than BioASQ which provides an additional challenge to the top two QA models, as per the results. We release our code and our dataset publicly to encourage further research.

Applications of Gaussian Processes at Extreme Lengthscales: From Molecules to Black Holes

In many areas of the observational and experimental sciences data is scarce. Data observation in high-energy astrophysics is disrupted by celestial occlusions and limited telescope time while data derived from laboratory experiments in synthetic chemistry and materials science is time and cost-intensive to collect. On the other hand, knowledge about the data-generation mechanism is often available in the sciences, such as the measurement error of a piece of laboratory apparatus. Both characteristics, small data and knowledge of the underlying physics, make Gaussian processes (GPs) ideal candidates for fitting such datasets. GPs can make predictions with consideration of uncertainty, for example in the virtual screening of molecules and materials, and can also make inferences about incomplete data such as the latent emission signature from a black hole accretion disc. Furthermore, GPs are currently the workhorse model for Bayesian optimisation, a methodology foreseen to be a guide for laboratory experiments in scientific discovery campaigns. The first contribution of this thesis is to use GP modelling to reason about the latent emission signature from the Seyfert galaxy Markarian 335, and by extension, to reason about the applicability of various theoretical models of black hole accretion discs. The second contribution is to extend the GP framework to molecular and chemical reaction representations and to provide an open-source software library to enable the framework to be used by scientists. The third contribution is to leverage GPs to discover novel and performant photoswitch molecules. The fourth contribution is to introduce a Bayesian optimisation scheme capable of modelling aleatoric uncertainty to facilitate the identification of material compositions that possess intrinsic robustness to large scale fabrication processes.

Mathematical Capabilities of ChatGPT

We investigate the mathematical capabilities of ChatGPT by testing it on publicly available datasets, as well as hand-crafted ones, and measuring its performance against other models trained on a mathematical corpus, such as Minerva. We also test whether ChatGPT can be a useful assistant to professional mathematicians by emulating various use cases that come up in the daily professional activities of mathematicians (question answering, theorem searching). In contrast to formal mathematics, where large databases of formal proofs are available (e.g., the Lean Mathematical Library), current datasets of natural-language mathematics, used to benchmark language models, only cover elementary mathematics. We address this issue by introducing a new dataset: GHOSTS. It is the first natural-language dataset made and curated by working researchers in mathematics that (1) aims to cover graduate-level mathematics and (2) provides a holistic overview of the mathematical capabilities of language models. We benchmark ChatGPT on GHOSTS and evaluate performance against fine-grained criteria. We make this new dataset publicly available to assist a community-driven comparison of ChatGPT with (future) large language models in terms of advanced mathematical comprehension. We conclude that contrary to many positive reports in the media (a potential case of selection bias), ChatGPT's mathematical abilities are significantly below those of an average mathematics graduate student. Our results show that ChatGPT often understands the question but fails to provide correct solutions. Hence, if your goal is to use it to pass a university exam, you would be better off copying from your average peer!

GAUCHE: A Library for Gaussian Processes in Chemistry

We introduce GAUCHE, a library for GAUssian processes in CHEmistry. Gaussian processes have long been a cornerstone of probabilistic machine learning, affording particular advantages for uncertainty quantification and Bayesian optimisation. Extending Gaussian processes to chemical representations, however, is nontrivial, necessitating kernels defined over structured inputs such as graphs, strings and bit vectors. By defining such kernels in GAUCHE, we seek to open the door to powerful tools for uncertainty quantification and Bayesian optimisation in chemistry. Motivated by scenarios frequently encountered in experimental chemistry, we showcase applications for GAUCHE in molecular discovery and chemical reaction optimisation. The codebase is made available at https://github.com/leojklarner/gauche

Extracting associations and meanings of objects depicted in artworks through bi-modal deep networks

We present a novel bi-modal system based on deep networks to address the problem of learning associations and simple meanings of objects depicted in "authored" images, such as fine art paintings and drawings. Our overall system processes both the images and associated texts in order to learn associations between images of individual objects, their identities and the abstract meanings they signify. Unlike past deep nets that describe depicted objects and infer predicates, our system identifies meaning-bearing objects ("signifiers") and their associations ("signifieds") as well as basic overall meanings for target artworks. Our system had precision of 48% and recall of 78% with an F1 metric of 0.6 on a curated set of Dutch vanitas paintings, a genre celebrated for its concentration on conveying a meaning of great import at the time of their execution. We developed and tested our system on fine art paintings but our general methods can be applied to other authored images.

Hierarchical Graph-Convolutional Variational AutoEncoding for Generative Modelling of Human Motion

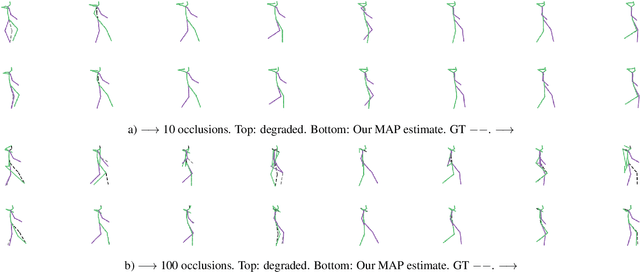
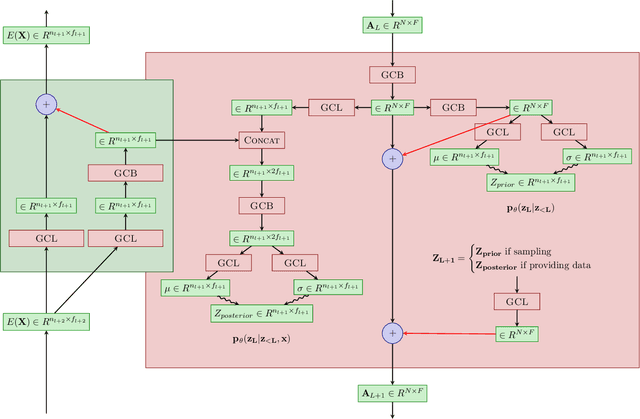
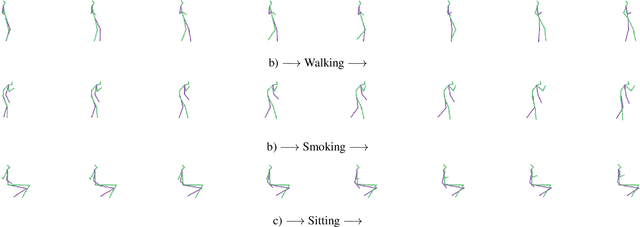
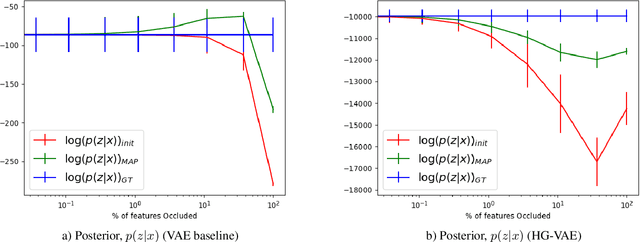
Models of human motion commonly focus either on trajectory prediction or action classification but rarely both. The marked heterogeneity and intricate compositionality of human motion render each task vulnerable to the data degradation and distributional shift common to real-world scenarios. A sufficiently expressive generative model of action could in theory enable data conditioning and distributional resilience within a unified framework applicable to both tasks. Here we propose a novel architecture based on hierarchical variational autoencoders and deep graph convolutional neural networks for generating a holistic model of action over multiple time-scales. We show this Hierarchical Graph-convolutional Variational Autoencoder (HG-VAE) to be capable of generating coherent actions, detecting out-of-distribution data, and imputing missing data by gradient ascent on the model's posterior. Trained and evaluated on H3.6M and the largest collection of open source human motion data, AMASS, we show HG-VAE can facilitate downstream discriminative learning better than baseline models.

Data Considerations in Graph Representation Learning for Supply Chain Networks

Supply chain network data is a valuable asset for businesses wishing to understand their ethical profile, security of supply, and efficiency. Possession of a dataset alone however is not a sufficient enabler of actionable decisions due to incomplete information. In this paper, we present a graph representation learning approach to uncover hidden dependency links that focal companies may not be aware of. To the best of our knowledge, our work is the first to represent a supply chain as a heterogeneous knowledge graph with learnable embeddings. We demonstrate that our representation facilitates state-of-the-art performance on link prediction of a global automotive supply chain network using a relational graph convolutional network. It is anticipated that our method will be directly applicable to businesses wishing to sever links with nefarious entities and mitigate risk of supply failure. More abstractly, it is anticipated that our method will be useful to inform representation learning of supply chain networks for downstream tasks beyond link prediction.

High-Dimensional Bayesian Optimisation with Variational Autoencoders and Deep Metric Learning

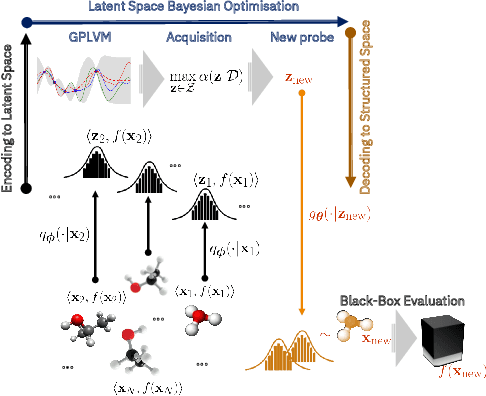
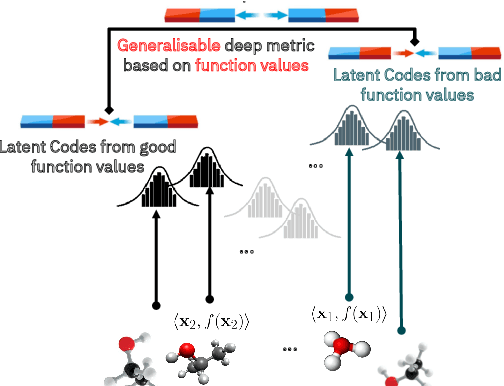
We introduce a method based on deep metric learning to perform Bayesian optimisation over high-dimensional, structured input spaces using variational autoencoders (VAEs). By extending ideas from supervised deep metric learning, we address a longstanding problem in high-dimensional VAE Bayesian optimisation, namely how to enforce a discriminative latent space as an inductive bias. Importantly, we achieve such an inductive bias using just 1% of the available labelled data relative to previous work, highlighting the sample efficiency of our approach. As a theoretical contribution, we present a proof of vanishing regret for our method. As an empirical contribution, we present state-of-the-art results on real-world high-dimensional black-box optimisation problems including property-guided molecule generation. It is the hope that the results presented in this paper can act as a guiding principle for realising effective high-dimensional Bayesian optimisation.