Reasoning over mathematical objects: on-policy reward modeling and test time aggregation

The ability to precisely derive mathematical objects is a core requirement for downstream STEM applications, including mathematics, physics, and chemistry, where reasoning must culminate in formally structured expressions. Yet, current LM evaluations of mathematical and scientific reasoning rely heavily on simplified answer formats such as numerical values or multiple choice options due to the convenience of automated assessment. In this paper we provide three contributions for improving reasoning over mathematical objects: (i) we build and release training data and benchmarks for deriving mathematical objects, the Principia suite; (ii) we provide training recipes with strong LLM-judges and verifiers, where we show that on-policy judge training boosts performance; (iii) we show how on-policy training can also be used to scale test-time compute via aggregation. We find that strong LMs such as Qwen3-235B and o3 struggle on Principia, while our training recipes can bring significant improvements over different LLM backbones, while simultaneously improving results on existing numerical and MCQA tasks, demonstrating cross-format generalization of reasoning abilities.

Argument Reconstruction as Supervision for Critical Thinking in LLMs

To think critically about arguments, human learners are trained to identify, reconstruct, and evaluate arguments. Argument reconstruction is especially important because it makes an argument's underlying inferences explicit. However, it remains unclear whether LLMs can similarly enhance their critical thinking ability by learning to reconstruct arguments. To address this question, we introduce a holistic framework with three contributions. We (1) propose an engine that automatically reconstructs arbitrary arguments (GAAR), (2) synthesize a new high-quality argument reconstruction dataset (Arguinas) using the GAAR engine, and (3) investigate whether learning argument reconstruction benefits downstream critical thinking tasks. Our experimental results show that, across seven critical thinking tasks, models trained to learn argument reconstruction outperform models that do not, with the largest performance gains observed when training on the proposed Arguinas dataset. The source code and dataset will be publicly available.

Mind the Sim2Real Gap in User Simulation for Agentic Tasks

As NLP evaluation shifts from static benchmarks to multi-turn interactive settings, LLM-based simulators have become widely used as user proxies, serving two roles: generating user turns and providing evaluation signals. Yet, these simulations are frequently assumed to be faithful to real human behaviors, often without rigorous verification. We formalize the Sim2Real gap in user simulation and present the first study running the full $τ$-bench protocol with real humans (451 participants, 165 tasks), benchmarking 31 LLM simulators across proprietary, open-source, and specialized families using the User-Sim Index (USI), a metric we introduce to quantify how well LLM simulators resemble real user interactive behaviors and feedback. Behaviorally, LLM simulators are excessively cooperative, stylistically uniform, and lack realistic frustration or ambiguity, creating an "easy mode" that inflates agent success rates above the human baseline. In evaluations, real humans provide nuanced judgments across eight quality dimensions while simulated users produce uniformly more positive feedback; rule-based rewards are failing to capture rich feedback signals generated by human users. Overall, higher general model capability does not necessarily yield more faithful user simulation. These findings highlight the importance of human validation when using LLM-based user simulators in the agent development cycle and motivate improved models for user simulation.

GradAlign: Gradient-Aligned Data Selection for LLM Reinforcement Learning

Reinforcement learning (RL) has become a central post-training paradigm for large language models (LLMs), but its performance is highly sensitive to the quality of training problems. This sensitivity stems from the non-stationarity of RL: rollouts are generated by an evolving policy, and learning is shaped by exploration and reward feedback, unlike supervised fine-tuning (SFT) with fixed trajectories. As a result, prior work often relies on manual curation or simple heuristic filters (e.g., accuracy), which can admit incorrect or low-utility problems. We propose GradAlign, a gradient-aligned data selection method for LLM reinforcement learning that uses a small, trusted validation set to prioritize training problems whose policy gradients align with validation gradients, yielding an adaptive curriculum. We evaluate GradAlign across three challenging data regimes: unreliable reward signals, distribution imbalance, and low-utility training corpus, showing that GradAlign consistently outperforms existing baselines, underscoring the importance of directional gradient signals in navigating non-stationary policy optimization and yielding more stable training and improved final performance. We release our implementation at https://github.com/StigLidu/GradAlign

Reasoning with Latent Tokens in Diffusion Language Models

Discrete diffusion models have recently become competitive with autoregressive models for language modeling, even outperforming them on reasoning tasks requiring planning and global coherence, but they require more computation at inference time. We trace this trade-off to a key mechanism: diffusion models are trained to jointly predict a distribution over all unknown tokens, including those that will not actually be decoded in the current step. Ablating this joint prediction yields faster inference but degrades performance, revealing that accurate prediction at the decoded position relies on joint reasoning about the distribution of undecoded tokens. We interpret these as latent tokens and introduce a method for modulating their number, demonstrating empirically that this enables a smooth tradeoff between inference speed and sample quality. Furthermore, we demonstrate that latent tokens can be introduced into autoregressive models through an auxiliary multi-token prediction objective, yielding substantial improvements on the same reasoning tasks where they have traditionally struggled. Our results suggest that latent tokens, while arising naturally in diffusion, represent a general mechanism for improving performance on tasks requiring global coherence or lookahead.

Propose, Solve, Verify: Self-Play Through Formal Verification

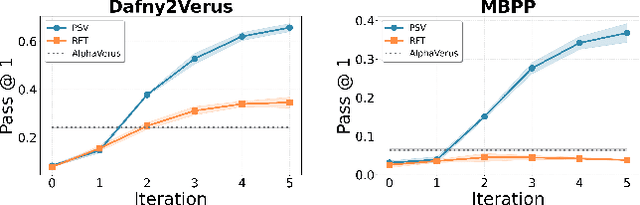
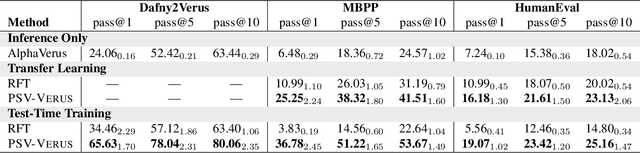
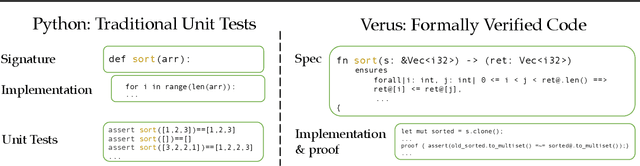
Training models through self-play alone (without any human data) has been a longstanding goal in AI, but its effectiveness for training large language models remains unclear, particularly in code generation where rewards based on unit tests are brittle and prone to error propagation. We study self-play in the verified code generation setting, where formal verification provides reliable correctness signals. We introduce Propose, Solve, Verify (PSV) a simple self-play framework where formal verification signals are used to create a proposer capable of generating challenging synthetic problems and a solver trained via expert iteration. We use PSV to train PSV-Verus, which across three benchmarks improves pass@1 by up to 9.6x over inference-only and expert-iteration baselines. We show that performance scales with the number of generated questions and training iterations, and through ablations identify formal verification and difficulty-aware proposal as essential ingredients for successful self-play.

OptimalThinkingBench: Evaluating Over and Underthinking in LLMs

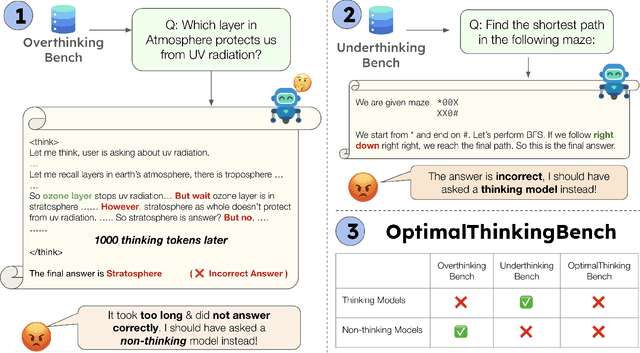
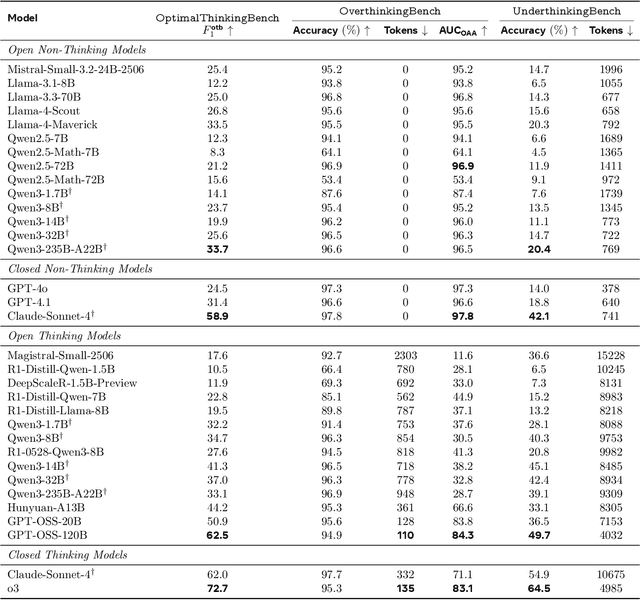
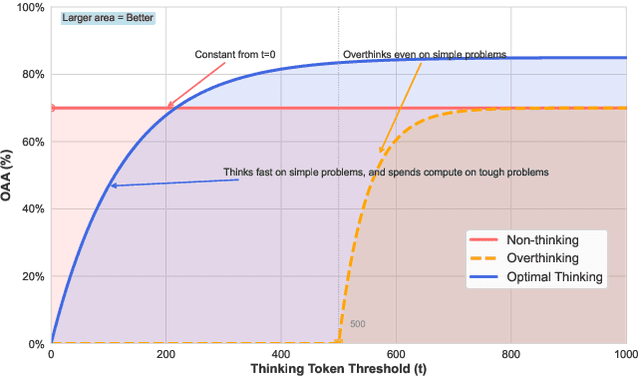
Thinking LLMs solve complex tasks at the expense of increased compute and overthinking on simpler problems, while non-thinking LLMs are faster and cheaper but underthink on harder reasoning problems. This has led to the development of separate thinking and non-thinking LLM variants, leaving the onus of selecting the optimal model for each query on the end user. In this work, we introduce OptimalThinkingBench, a unified benchmark that jointly evaluates overthinking and underthinking in LLMs and also encourages the development of optimally-thinking models that balance performance and efficiency. Our benchmark comprises two sub-benchmarks: OverthinkingBench, featuring simple queries in 72 domains, and UnderthinkingBench, containing 11 challenging reasoning tasks. Using novel thinking-adjusted accuracy metrics, we perform extensive evaluation of 33 different thinking and non-thinking models and show that no model is able to optimally think on our benchmark. Thinking models often overthink for hundreds of tokens on the simplest user queries without improving performance. In contrast, large non-thinking models underthink, often falling short of much smaller thinking models. We further explore several methods to encourage optimal thinking, but find that these approaches often improve on one sub-benchmark at the expense of the other, highlighting the need for better unified and optimal models in the future.

Premise Selection for a Lean Hammer

Neural methods are transforming automated reasoning for proof assistants, yet integrating these advances into practical verification workflows remains challenging. Hammers are tools that interface with external automatic theorem provers to automate tedious reasoning steps. They have dramatically improved productivity in proof assistants, but the Lean proof assistant still does not have a hammer despite its growing popularity. We present LeanHammer, the first end-to-end domain-general hammer for Lean, built on a novel neural premise selection system for a hammer in dependent type theory. Unlike existing Lean premise selectors, our approach dynamically adapts to user-specific contexts and combines with symbolic proof search and reconstruction to create a practical hammer. With comprehensive evaluations, we show that our premise selector enables LeanHammer to solve 21\% more goals relative to existing premise selectors, and generalize well to diverse domains. Our work bridges the gap between neural retrieval and symbolic reasoning, making formal verification more accessible to researchers and practitioners.

The CoT Encyclopedia: Analyzing, Predicting, and Controlling how a Reasoning Model will Think

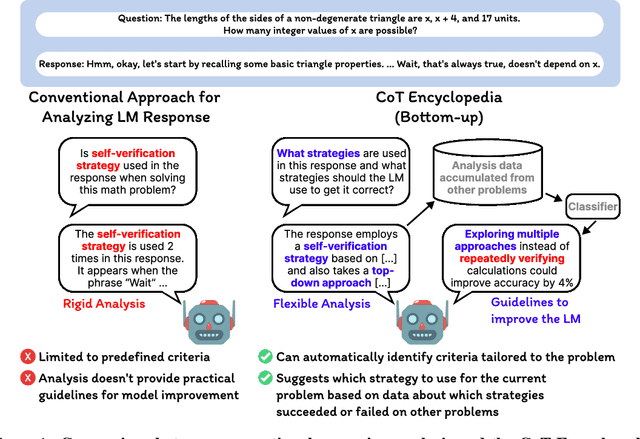
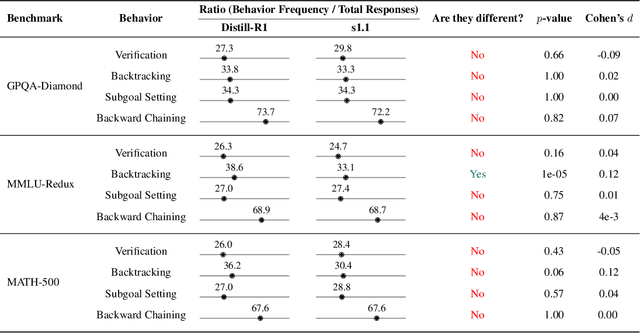
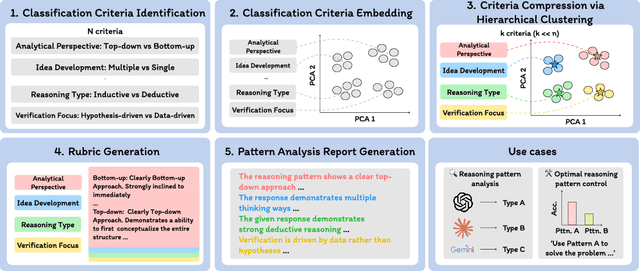
Long chain-of-thought (CoT) is an essential ingredient in effective usage of modern large language models, but our understanding of the reasoning strategies underlying these capabilities remains limited. While some prior works have attempted to categorize CoTs using predefined strategy types, such approaches are constrained by human intuition and fail to capture the full diversity of model behaviors. In this work, we introduce the CoT Encyclopedia, a bottom-up framework for analyzing and steering model reasoning. Our method automatically extracts diverse reasoning criteria from model-generated CoTs, embeds them into a semantic space, clusters them into representative categories, and derives contrastive rubrics to interpret reasoning behavior. Human evaluations show that this framework produces more interpretable and comprehensive analyses than existing methods. Moreover, we demonstrate that this understanding enables performance gains: we can predict which strategy a model is likely to use and guide it toward more effective alternatives. Finally, we provide practical insights, such as that training data format (e.g., free-form vs. multiple-choice) has a far greater impact on reasoning behavior than data domain, underscoring the importance of format-aware model design.

Scaling Evaluation-time Compute with Reasoning Models as Process Evaluators

As language model (LM) outputs get more and more natural, it is becoming more difficult than ever to evaluate their quality. Simultaneously, increasing LMs' "thinking" time through scaling test-time compute has proven an effective technique to solve challenging problems in domains such as math and code. This raises a natural question: can an LM's evaluation capability also be improved by spending more test-time compute? To answer this, we investigate employing reasoning models-LMs that natively generate long chain-of-thought reasoning-as evaluators. Specifically, we examine methods to leverage more test-time compute by (1) using reasoning models, and (2) prompting these models to evaluate not only the response as a whole (i.e., outcome evaluation) but also assess each step in the response separately (i.e., process evaluation). In experiments, we observe that the evaluator's performance improves monotonically when generating more reasoning tokens, similar to the trends observed in LM-based generation. Furthermore, we use these more accurate evaluators to rerank multiple generations, and demonstrate that spending more compute at evaluation time can be as effective as using more compute at generation time in improving an LM's problem-solving capability.