Bryan Parno
Propose, Solve, Verify: Self-Play Through Formal Verification
Dec 20, 2025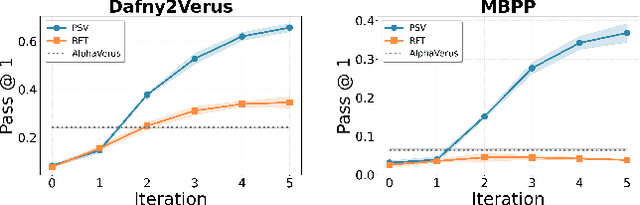
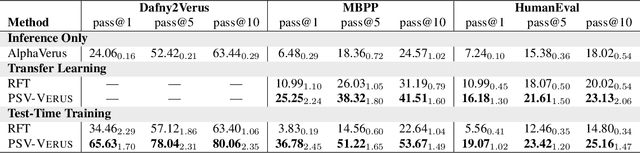
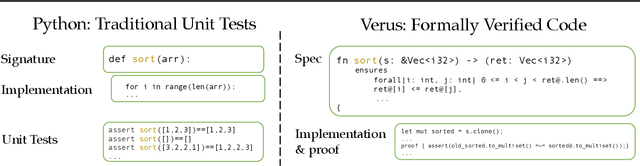

Abstract:Training models through self-play alone (without any human data) has been a longstanding goal in AI, but its effectiveness for training large language models remains unclear, particularly in code generation where rewards based on unit tests are brittle and prone to error propagation. We study self-play in the verified code generation setting, where formal verification provides reliable correctness signals. We introduce Propose, Solve, Verify (PSV) a simple self-play framework where formal verification signals are used to create a proposer capable of generating challenging synthetic problems and a solver trained via expert iteration. We use PSV to train PSV-Verus, which across three benchmarks improves pass@1 by up to 9.6x over inference-only and expert-iteration baselines. We show that performance scales with the number of generated questions and training iterations, and through ablations identify formal verification and difficulty-aware proposal as essential ingredients for successful self-play.
AlphaVerus: Bootstrapping Formally Verified Code Generation through Self-Improving Translation and Treefinement
Dec 09, 2024Abstract:Automated code generation with large language models has gained significant traction, but there remains no guarantee on the correctness of generated code. We aim to use formal verification to provide mathematical guarantees that the generated code is correct. However, generating formally verified code with LLMs is hindered by the scarcity of training data and the complexity of formal proofs. To tackle this challenge, we introduce AlphaVerus, a self-improving framework that bootstraps formally verified code generation by iteratively translating programs from a higher-resource language and leveraging feedback from a verifier. AlphaVerus operates in three phases: exploration of candidate translations, Treefinement -- a novel tree search algorithm for program refinement using verifier feedback, and filtering misaligned specifications and programs to prevent reward hacking. Through this iterative process, AlphaVerus enables a LLaMA-3.1-70B model to generate verified code without human intervention or model finetuning. AlphaVerus shows an ability to generate formally verified solutions for HumanEval and MBPP, laying the groundwork for truly trustworthy code-generation agents.
Self-Repairing Neural Networks: Provable Safety for Deep Networks via Dynamic Repair
Jul 23, 2021


Abstract:Neural networks are increasingly being deployed in contexts where safety is a critical concern. In this work, we propose a way to construct neural network classifiers that dynamically repair violations of non-relational safety constraints called safe ordering properties. Safe ordering properties relate requirements on the ordering of a network's output indices to conditions on their input, and are sufficient to express most useful notions of non-relational safety for classifiers. Our approach is based on a novel self-repairing layer, which provably yields safe outputs regardless of the characteristics of its input. We compose this layer with an existing network to construct a self-repairing network (SR-Net), and show that in addition to providing safe outputs, the SR-Net is guaranteed to preserve the accuracy of the original network. Notably, our approach is independent of the size and architecture of the network being repaired, depending only on the specified property and the dimension of the network's output; thus it is scalable to large state-of-the-art networks. We show that our approach can be implemented using vectorized computations that execute efficiently on a GPU, introducing run-time overhead of less than one millisecond on current hardware -- even on large, widely-used networks containing hundreds of thousands of neurons and millions of parameters.
Fast Geometric Projections for Local Robustness Certification
Feb 12, 2020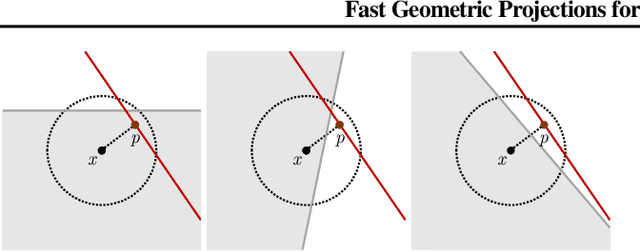
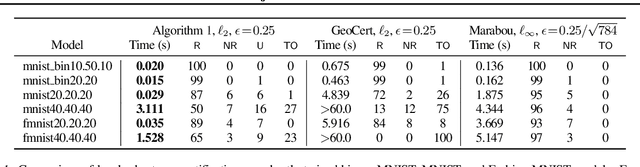
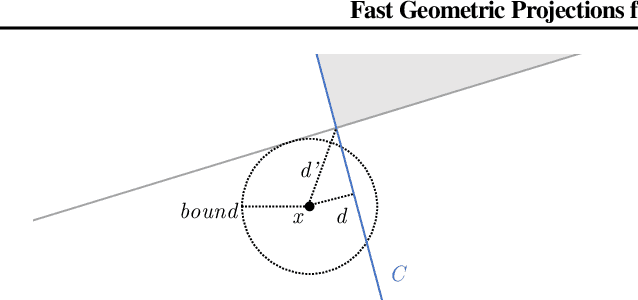
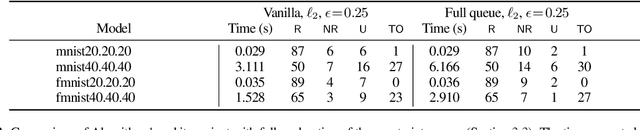
Abstract:Local robustness ensures that a model classifies all inputs within an $\epsilon$-ball consistently, which precludes various forms of adversarial inputs. In this paper, we present a fast procedure for checking local robustness in feed-forward neural networks with piecewise linear activation functions. The key insight is that such networks partition the input space into a polyhedral complex such that the network is linear inside each polyhedral region; hence, a systematic search for decision boundaries within the regions around a given input is sufficient for assessing robustness. Crucially, we show how these regions can be analyzed using geometric projections instead of expensive constraint solving, thus admitting an efficient, highly-parallel GPU implementation at the price of incompleteness, which can be addressed by falling back on prior approaches. Empirically, we find that incompleteness is not often an issue, and that our method performs one to two orders of magnitude faster than existing robustness-certification techniques based on constraint solving.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge