Fast Geometric Projections for Local Robustness Certification

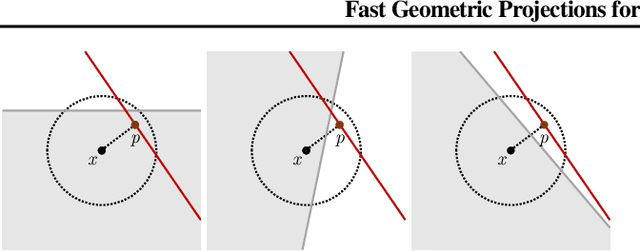
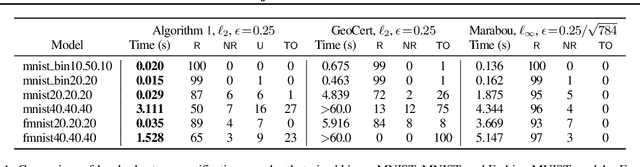
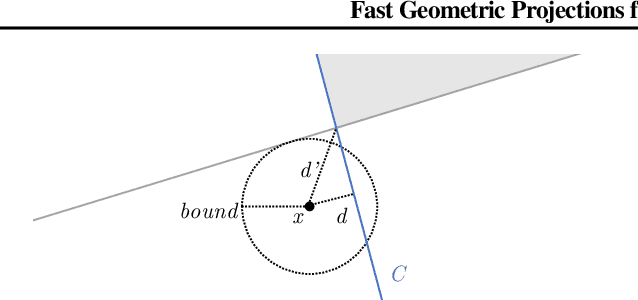
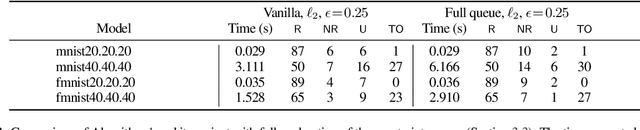
Local robustness ensures that a model classifies all inputs within an $\epsilon$-ball consistently, which precludes various forms of adversarial inputs. In this paper, we present a fast procedure for checking local robustness in feed-forward neural networks with piecewise linear activation functions. The key insight is that such networks partition the input space into a polyhedral complex such that the network is linear inside each polyhedral region; hence, a systematic search for decision boundaries within the regions around a given input is sufficient for assessing robustness. Crucially, we show how these regions can be analyzed using geometric projections instead of expensive constraint solving, thus admitting an efficient, highly-parallel GPU implementation at the price of incompleteness, which can be addressed by falling back on prior approaches. Empirically, we find that incompleteness is not often an issue, and that our method performs one to two orders of magnitude faster than existing robustness-certification techniques based on constraint solving.