Characterizing initial human-AI proof formalization workflows

For centuries, human mathematicians have written proofs to substantiate their mathematical arguments; yet, the ability to automatically verify the validity of proofs has long been a challenge. Advances in AI systems' ability to generate code and engage in increasingly high-level mathematical reasoning promise to transform people's ability to formalize and thereby verify proofs. While many works focus on benchmarking the current frontier, we instead study how people use these tools. We conduct a mixed-methods analysis into the initial impact of AI on people's formalization workflows: what people claim they want, what they see as the barriers to those visions, and how they actually use and adapt AI in practice. A qualitative survey shows that people's preferences are diverse, but with a general desire for AI assistance in formalization that preserves high-level human control over the proof discovery process. To assess how people actually engage with AI for formalization under such limitations, we conduct a controlled user study in which participants formalize informal math problems and their proofs, with and without AI, across a range of mathematical problems at varying levels of difficulty and domains. Despite limitations of the tools at the time for autoformalization, participants tend to attain higher formalization accuracy when allowed access to AI tools than when formalizing on their own, with most participants flexibly choosing to use multiple different AI tools. Taken together, our work sheds light on the early stages of AI integration into formalization workflows, involving an intimate interplay of human and AI engagement.

Faster Predictive Coding Networks via Better Initialization

Research aimed at scaling up neuroscience inspired learning algorithms for neural networks is accelerating. Recently, a key research area has been the study of energy-based learning algorithms such as predictive coding, due to their versatility and mathematical grounding. However, the applicability of such methods is held back by the large computational requirements caused by their iterative nature. In this work, we address this problem by showing that the choice of initialization of the neurons in a predictive coding network matters significantly and can notably reduce the required training times. Consequently, we propose a new initialization technique for predictive coding networks that aims to preserve the iterative progress made on previous training samples. Our approach suggests a promising path toward reconciling the disparities between predictive coding and backpropagation in terms of computational efficiency and final performance. In fact, our experiments demonstrate substantial improvements in convergence speed and final test loss in both supervised and unsupervised settings.

Data for Mathematical Copilots: Better Ways of Presenting Proofs for Machine Learning

The suite of datasets commonly used to train and evaluate the mathematical capabilities of AI-based mathematical copilots (primarily large language models) exhibit several shortcomings. These limitations include a restricted scope of mathematical complexity, typically not exceeding lower undergraduate-level mathematics, binary rating protocols and other issues, which makes comprehensive proof-based evaluation suites difficult. We systematically explore these limitations and contend that enhancing the capabilities of large language models, or any forthcoming advancements in AI-based mathematical assistants (copilots or "thought partners"), necessitates a paradigm shift in the design of mathematical datasets and the evaluation criteria of mathematical ability: It is necessary to move away from result-based datasets (theorem statement to theorem proof) and convert the rich facets of mathematical research practice to data LLMs can train on. Examples of these are mathematical workflows (sequences of atomic, potentially subfield-dependent tasks that are often performed when creating new mathematics), which are an important part of the proof-discovery process. Additionally, we advocate for mathematical dataset developers to consider the concept of "motivated proof", introduced by G. P\'olya in 1949, which can serve as a blueprint for datasets that offer a better proof learning signal, alleviating some of the mentioned limitations. Lastly, we introduce math datasheets for datasets, extending the general, dataset-agnostic variants of datasheets: We provide a questionnaire designed specifically for math datasets that we urge dataset creators to include with their datasets. This will make creators aware of potential limitations of their datasets while at the same time making it easy for readers to assess it from the point of view of training and evaluating mathematical copilots.

Newclid: A User-Friendly Replacement for AlphaGeometry

We introduce a new symbolic solver for geometry, called Newclid, which is based on AlphaGeometry. Newclid contains a symbolic solver called DDARN (derived from DDAR-Newclid), which is a significant refactoring and upgrade of AlphaGeometry's DDAR symbolic solver by being more user-friendly - both for the end user as well as for a programmer wishing to extend the codebase. For the programmer, improvements include a modularized codebase and new debugging and visualization tools. For the user, Newclid contains a new command line interface (CLI) that provides interfaces for agents to guide DDARN. DDARN is flexible with respect to its internal reasoning, which can be steered by agents. Further, we support input from GeoGebra to make Newclid accessible for educational contexts. Further, the scope of problems that Newclid can solve has been expanded to include the ability to have an improved understanding of metric geometry concepts (length, angle) and to use theorems such as the Pythagorean theorem in proofs. Bugs have been fixed, and reproducibility has been improved. Lastly, we re-evaluated the five remaining problems from the original AG-30 dataset that AlphaGeometry was not able to solve and contrasted them with the abilities of DDARN, running in breadth-first-search agentic mode (which corresponds to how DDARN runs by default), finding that DDARN solves an additional problem. We have open-sourced our code under: https://github.com/LMCRC/Newclid

Dimension-independent learning rates for high-dimensional classification problems

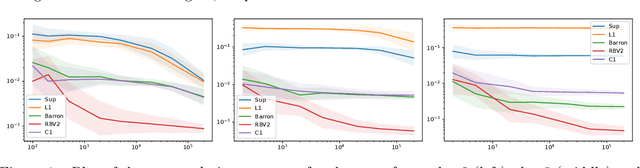
We study the problem of approximating and estimating classification functions that have their decision boundary in the $RBV^2$ space. Functions of $RBV^2$ type arise naturally as solutions of regularized neural network learning problems and neural networks can approximate these functions without the curse of dimensionality. We modify existing results to show that every $RBV^2$ function can be approximated by a neural network with bounded weights. Thereafter, we prove the existence of a neural network with bounded weights approximating a classification function. And we leverage these bounds to quantify the estimation rates. Finally, we present a numerical study that analyzes the effect of different regularity conditions on the decision boundaries.

Benchmarking Predictive Coding Networks -- Made Simple

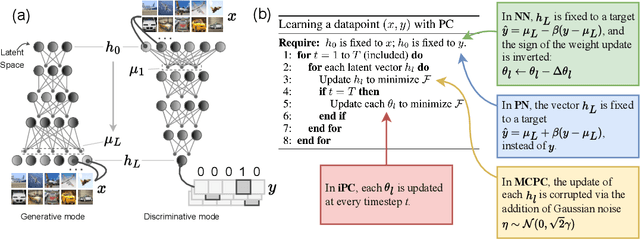
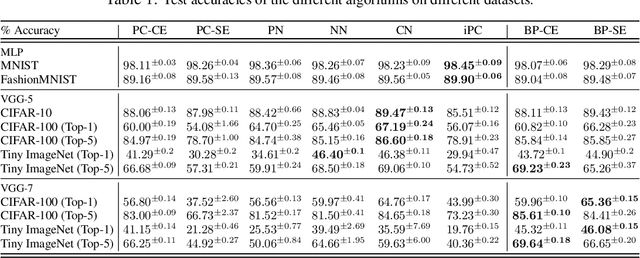
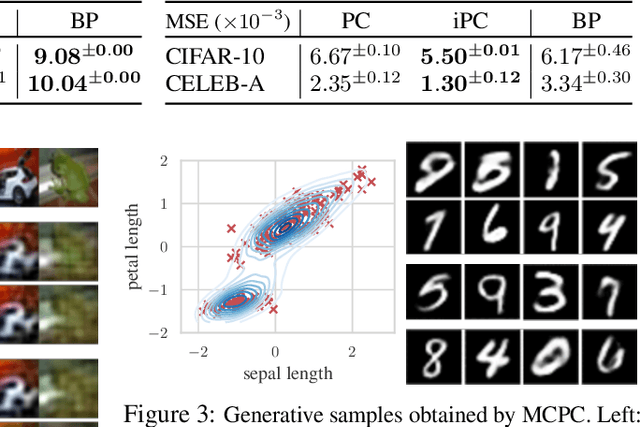
In this work, we tackle the problems of efficiency and scalability for predictive coding networks in machine learning. To do so, we first propose a library called PCX, whose focus lies on performance and simplicity, and provides a user-friendly, deep-learning oriented interface. Second, we use PCX to implement a large set of benchmarks for the community to use for their experiments. As most works propose their own tasks and architectures, do not compare one against each other, and focus on small-scale tasks, a simple and fast open-source library adopted by the whole community would address all of these concerns. Third, we perform extensive benchmarks using multiple algorithms, setting new state-of-the-art results in multiple tasks and datasets, as well as highlighting limitations inherent to PC that should be addressed. Thanks to the efficiency of PCX, we are able to analyze larger architectures than commonly used, providing baselines to galvanize community efforts towards one of the main open problems in the field: scalability. The code for PCX is available at \textit{https://github.com/liukidar/pcax}.

Language Models as Science Tutors

NLP has recently made exciting progress toward training language models (LMs) with strong scientific problem-solving skills. However, model development has not focused on real-life use-cases of LMs for science, including applications in education that require processing long scientific documents. To address this, we introduce TutorEval and TutorChat. TutorEval is a diverse question-answering benchmark consisting of questions about long chapters from STEM textbooks, written by experts. TutorEval helps measure real-life usability of LMs as scientific assistants, and it is the first benchmark combining long contexts, free-form generation, and multi-disciplinary scientific knowledge. Moreover, we show that fine-tuning base models with existing dialogue datasets leads to poor performance on TutorEval. Therefore, we create TutorChat, a dataset of 80,000 long synthetic dialogues about textbooks. We use TutorChat to fine-tune Llemma models with 7B and 34B parameters. These LM tutors specialized in math have a 32K-token context window, and they excel at TutorEval while performing strongly on GSM8K and MATH. Our datasets build on open-source materials, and we release our models, data, and evaluations.

Large Language Models for Mathematicians

Large language models (LLMs) such as ChatGPT have received immense interest for their general-purpose language understanding and, in particular, their ability to generate high-quality text or computer code. For many professions, LLMs represent an invaluable tool that can speed up and improve the quality of work. In this note, we discuss to what extent they can aid professional mathematicians. We first provide a mathematical description of the transformer model used in all modern language models. Based on recent studies, we then outline best practices and potential issues and report on the mathematical abilities of language models. Finally, we shed light on the potential of LMMs to change how mathematicians work.

The ARRT of Language-Models-as-a-Service: Overview of a New Paradigm and its Challenges

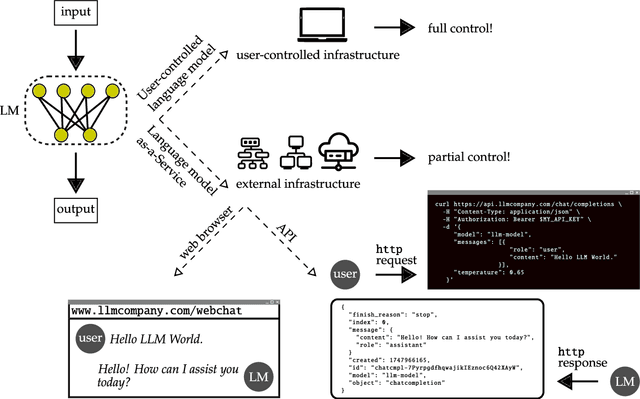
Some of the most powerful language models currently are proprietary systems, accessible only via (typically restrictive) web or software programming interfaces. This is the Language-Models-as-a-Service (LMaaS) paradigm. Contrasting with scenarios where full model access is available, as in the case of open-source models, such closed-off language models create specific challenges for evaluating, benchmarking, and testing them. This paper has two goals: on the one hand, we delineate how the aforementioned challenges act as impediments to the accessibility, replicability, reliability, and trustworthiness (ARRT) of LMaaS. We systematically examine the issues that arise from a lack of information about language models for each of these four aspects. We shed light on current solutions, provide some recommendations, and highlight the directions for future advancements. On the other hand, it serves as a one-stop-shop for the extant knowledge about current, major LMaaS, offering a synthesized overview of the licences and capabilities their interfaces offer.

Evaluating Language Models for Mathematics through Interactions

The standard methodology of evaluating large language models (LLMs) based on static pairs of inputs and outputs is insufficient for developing assistants: this kind of assessments fails to take into account the essential interactive element in their deployment, and therefore limits how we understand language model capabilities. We introduce CheckMate, an adaptable prototype platform for humans to interact with and evaluate LLMs. We conduct a study with CheckMate to evaluate three language models~(InstructGPT, ChatGPT, and GPT-4) as assistants in proving undergraduate-level mathematics, with a mixed cohort of participants from undergraduate students to professors of mathematics. We release the resulting interaction and rating dataset, MathConverse. By analysing MathConverse, we derive a preliminary taxonomy of human behaviours and uncover that despite a generally positive correlation, there are notable instances of divergence between correctness and perceived helpfulness in LLM generations, amongst other findings. Further, we identify useful scenarios and existing issues of GPT-4 in mathematical reasoning through a series of case studies contributed by expert mathematicians. We conclude with actionable takeaways for ML practitioners and mathematicians: models which communicate uncertainty, respond well to user corrections, are more interpretable and concise may constitute better assistants; interactive evaluation is a promising way to continually navigate the capability of these models; humans should be aware of language models' algebraic fallibility, and for that reason discern where they should be used.