Bidirectional predictive coding

Predictive coding (PC) is an influential computational model of visual learning and inference in the brain. Classical PC was proposed as a top-down generative model, where the brain actively predicts upcoming visual inputs, and inference minimises the prediction errors. Recent studies have also shown that PC can be formulated as a discriminative model, where sensory inputs predict neural activities in a feedforward manner. However, experimental evidence suggests that the brain employs both generative and discriminative inference, while unidirectional PC models show degraded performance in tasks requiring bidirectional processing. In this work, we propose bidirectional PC (bPC), a PC model that incorporates both generative and discriminative inference while maintaining a biologically plausible circuit implementation. We show that bPC matches or outperforms unidirectional models in their specialised generative or discriminative tasks, by developing an energy landscape that simultaneously suits both tasks. We also demonstrate bPC's superior performance in two biologically relevant tasks including multimodal learning and inference with missing information, suggesting that bPC resembles biological visual inference more closely.

Neural Associative Skill Memories for safer robotics and modelling human sensorimotor repertoires

Modern robots face challenges shared by humans, where machines must learn multiple sensorimotor skills and express them adaptively. Equipping robots with a human-like memory of how it feels to do multiple stereotypical movements can make robots more aware of normal operational states and help develop self-preserving safer robots. Associative Skill Memories (ASMs) aim to address this by linking movement primitives to sensory feedback, but existing implementations rely on hard-coded libraries of individual skills. A key unresolved problem is how a single neural network can learn a repertoire of skills while enabling fault detection and context-aware execution. Here we introduce Neural Associative Skill Memories (ASMs), a framework that utilises self-supervised predictive coding for temporal prediction to unify skill learning and expression, using biologically plausible learning rules. Unlike traditional ASMs which require explicit skill selection, Neural ASMs implicitly recognize and express skills through contextual inference, enabling fault detection across learned behaviours without an explicit skill selection mechanism. Compared to recurrent neural networks trained via backpropagation through time, our model achieves comparable qualitative performance in skill memory expression while using local learning rules and predicts a biologically relevant speed-accuracy trade-off during skill memory expression. This work advances the field of neurorobotics by demonstrating how predictive coding principles can model adaptive robot control and human motor preparation. By unifying fault detection, reactive control, skill memorisation and expression into a single energy-based architecture, Neural ASMs contribute to safer robotics and provide a computational lens to study biological sensorimotor learning.

Benchmarking Predictive Coding Networks -- Made Simple

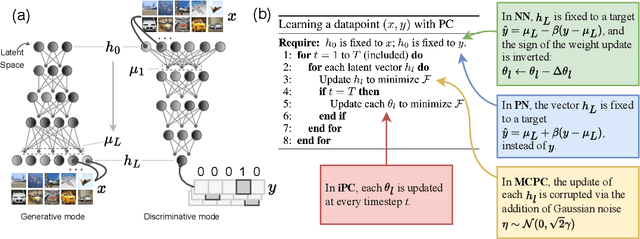
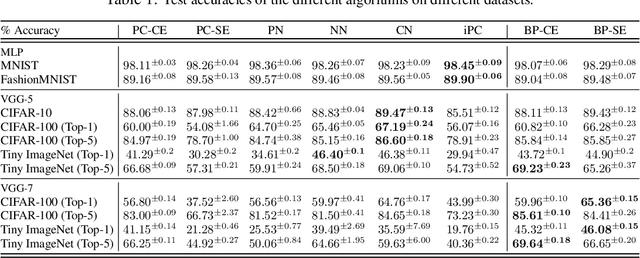
In this work, we tackle the problems of efficiency and scalability for predictive coding networks in machine learning. To do so, we first propose a library called PCX, whose focus lies on performance and simplicity, and provides a user-friendly, deep-learning oriented interface. Second, we use PCX to implement a large set of benchmarks for the community to use for their experiments. As most works propose their own tasks and architectures, do not compare one against each other, and focus on small-scale tasks, a simple and fast open-source library adopted by the whole community would address all of these concerns. Third, we perform extensive benchmarks using multiple algorithms, setting new state-of-the-art results in multiple tasks and datasets, as well as highlighting limitations inherent to PC that should be addressed. Thanks to the efficiency of PCX, we are able to analyze larger architectures than commonly used, providing baselines to galvanize community efforts towards one of the main open problems in the field: scalability. The code for PCX is available at \textit{https://github.com/liukidar/pcax}.

Sequential Memory with Temporal Predictive Coding

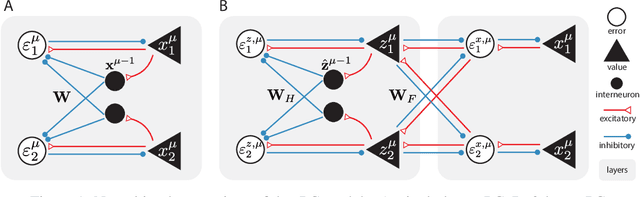
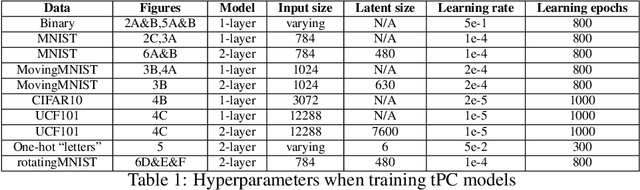
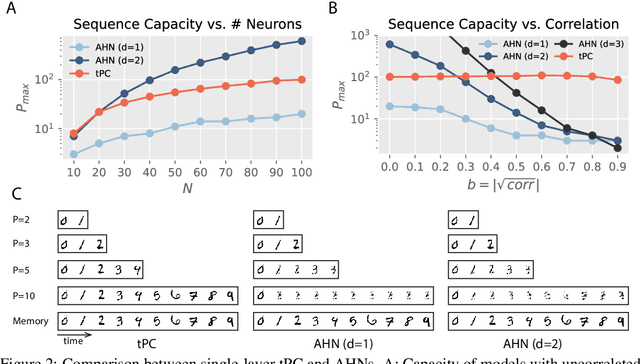
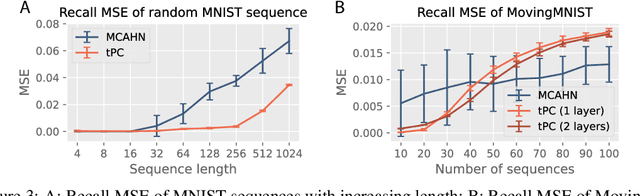
Memorizing the temporal order of event sequences is critical for the survival of biological agents. However, the computational mechanism underlying sequential memory in the brain remains unclear. Inspired by neuroscience theories and recent successes in applying predictive coding (PC) to static memory tasks, in this work we propose a novel PC-based model for sequential memory, called temporal predictive coding (tPC). We show that our tPC models can memorize and retrieve sequential inputs accurately with a biologically plausible neural implementation. Importantly, our analytical study reveals that tPC can be viewed as a classical Asymmetric Hopfield Network (AHN) with an implicit statistical whitening process, which leads to more stable performance in sequential memory tasks of structured inputs. Moreover, we find that tPC with a multi-layer structure can encode context-dependent information, thus distinguishing between repeating elements appearing in a sequence, a computation attributed to the hippocampus. Our work establishes a possible computational mechanism underlying sequential memory in the brain that can also be theoretically interpreted using existing memory model frameworks.

Biologically Plausible Training Mechanisms for Self-Supervised Learning in Deep Networks

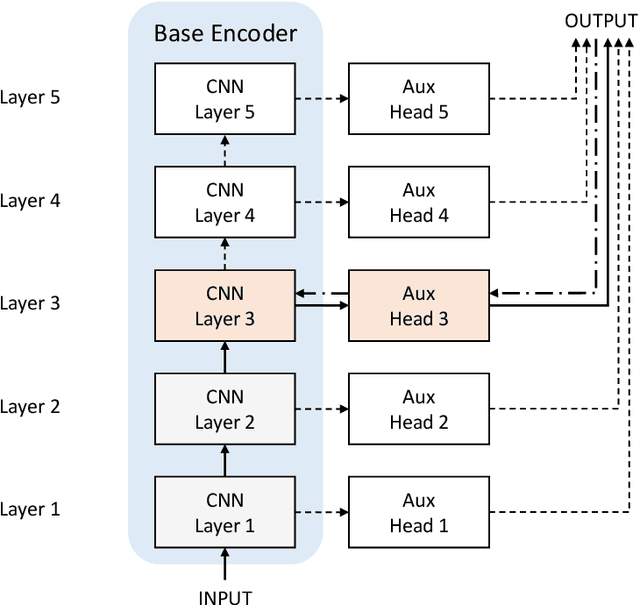
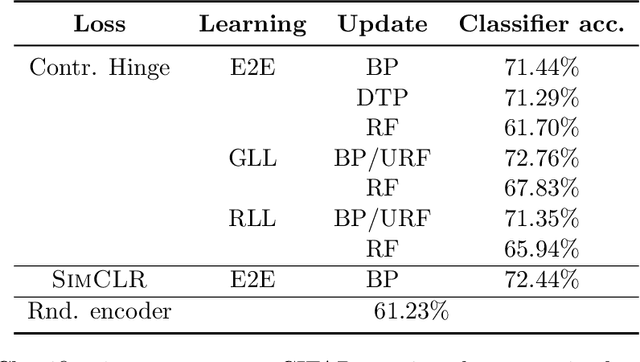
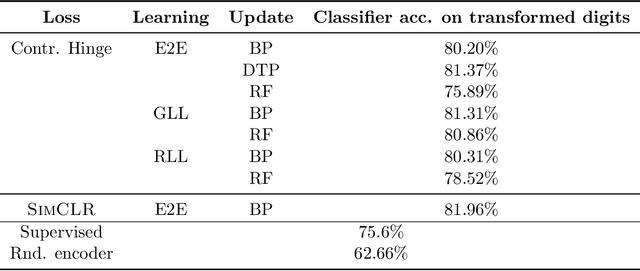
We develop biologically plausible training mechanisms for self-supervised learning (SSL) in deep networks. SSL, with a contrastive loss, is more natural as it does not require labelled data and its robustness to perturbations yields more adaptable embeddings. Moreover the perturbation of data required to create positive pairs for SSL is easily produced in a natural environment by observing objects in motion and with variable lighting over time. We propose a contrastive hinge based loss whose error involves simple local computations as opposed to the standard contrastive losses employed in the literature, which do not lend themselves easily to implementation in a network architecture due to complex computations involving ratios and inner products. Furthermore we show that learning can be performed with one of two more plausible alternatives to backpropagation. The first is difference target propagation (DTP), which trains network parameters using target-based local losses and employs a Hebbian learning rule, thus overcoming the biologically implausible symmetric weight problem in backpropagation. The second is simply layer-wise learning, where each layer is directly connected to a layer computing the loss error. The layers are either updated sequentially in a greedy fashion (GLL) or in random order (RLL), and each training stage involves a single hidden layer network. The one step backpropagation needed for each such network can either be altered with fixed random feedback weights as proposed in Lillicrap et al. (2016), or using updated random feedback as in Amit (2019). Both methods represent alternatives to the symmetric weight issue of backpropagation. By training convolutional neural networks (CNNs) with SSL and DTP, GLL or RLL, we find that our proposed framework achieves comparable performance to its implausible counterparts in both linear evaluation and transfer learning tasks.