Benchmarking Predictive Coding Networks -- Made Simple

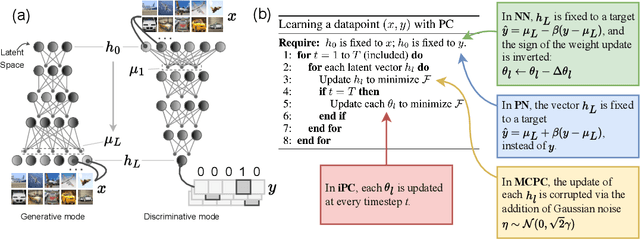
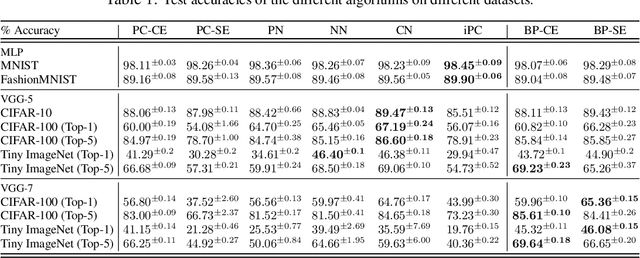
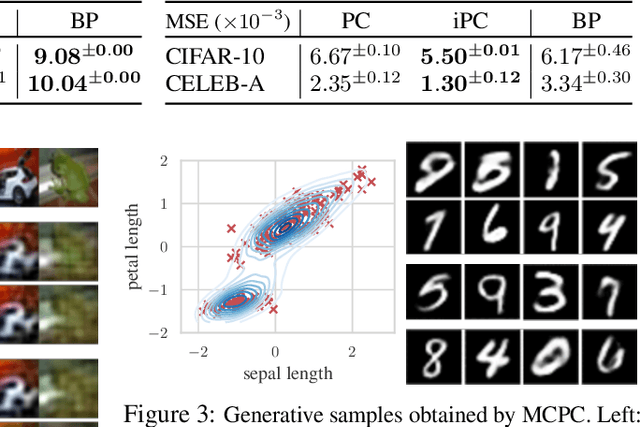
In this work, we tackle the problems of efficiency and scalability for predictive coding networks in machine learning. To do so, we first propose a library called PCX, whose focus lies on performance and simplicity, and provides a user-friendly, deep-learning oriented interface. Second, we use PCX to implement a large set of benchmarks for the community to use for their experiments. As most works propose their own tasks and architectures, do not compare one against each other, and focus on small-scale tasks, a simple and fast open-source library adopted by the whole community would address all of these concerns. Third, we perform extensive benchmarks using multiple algorithms, setting new state-of-the-art results in multiple tasks and datasets, as well as highlighting limitations inherent to PC that should be addressed. Thanks to the efficiency of PCX, we are able to analyze larger architectures than commonly used, providing baselines to galvanize community efforts towards one of the main open problems in the field: scalability. The code for PCX is available at \textit{https://github.com/liukidar/pcax}.

Causal Inference via Predictive Coding

Bayesian and causal inference are fundamental processes for intelligence. Bayesian inference models observations: what can be inferred about y if we observe a related variable x? Causal inference models interventions: if we directly change x, how will y change? Predictive coding is a neuroscience-inspired method for performing Bayesian inference on continuous state variables using local information only. In this work, we go beyond Bayesian inference, and show how a simple change in the inference process of predictive coding enables interventional and counterfactual inference in scenarios where the causal graph is known. We then extend our results, and show how predictive coding can be generalized to cases where this graph is unknown, and has to be inferred from data, hence performing causal discovery. What results is a novel and straightforward technique that allows us to perform end-to-end causal inference on predictive-coding-based structural causal models, and demonstrate its utility for potential applications in machine learning.

Mathematical Capabilities of ChatGPT

We investigate the mathematical capabilities of ChatGPT by testing it on publicly available datasets, as well as hand-crafted ones, and measuring its performance against other models trained on a mathematical corpus, such as Minerva. We also test whether ChatGPT can be a useful assistant to professional mathematicians by emulating various use cases that come up in the daily professional activities of mathematicians (question answering, theorem searching). In contrast to formal mathematics, where large databases of formal proofs are available (e.g., the Lean Mathematical Library), current datasets of natural-language mathematics, used to benchmark language models, only cover elementary mathematics. We address this issue by introducing a new dataset: GHOSTS. It is the first natural-language dataset made and curated by working researchers in mathematics that (1) aims to cover graduate-level mathematics and (2) provides a holistic overview of the mathematical capabilities of language models. We benchmark ChatGPT on GHOSTS and evaluate performance against fine-grained criteria. We make this new dataset publicly available to assist a community-driven comparison of ChatGPT with (future) large language models in terms of advanced mathematical comprehension. We conclude that contrary to many positive reports in the media (a potential case of selection bias), ChatGPT's mathematical abilities are significantly below those of an average mathematics graduate student. Our results show that ChatGPT often understands the question but fails to provide correct solutions. Hence, if your goal is to use it to pass a university exam, you would be better off copying from your average peer!

Predictive Coding beyond Gaussian Distributions

A large amount of recent research has the far-reaching goal of finding training methods for deep neural networks that can serve as alternatives to backpropagation (BP). A prominent example is predictive coding (PC), which is a neuroscience-inspired method that performs inference on hierarchical Gaussian generative models. These methods, however, fail to keep up with modern neural networks, as they are unable to replicate the dynamics of complex layers and activation functions. In this work, we solve this problem by generalizing PC to arbitrary probability distributions, enabling the training of architectures, such as transformers, that are hard to approximate with only Gaussian assumptions. We perform three experimental analyses. First, we study the gap between our method and the standard formulation of PC on multiple toy examples. Second, we test the reconstruction quality on variational autoencoders, where our method reaches the same reconstruction quality as BP. Third, we show that our method allows us to train transformer networks and achieve a performance comparable with BP on conditional language models. More broadly, this method allows neuroscience-inspired learning to be applied to multiple domains, since the internal distributions can be flexibly adapted to the data, tasks, and architectures used.

Learning on Arbitrary Graph Topologies via Predictive Coding

Training with backpropagation (BP) in standard deep learning consists of two main steps: a forward pass that maps a data point to its prediction, and a backward pass that propagates the error of this prediction back through the network. This process is highly effective when the goal is to minimize a specific objective function. However, it does not allow training on networks with cyclic or backward connections. This is an obstacle to reaching brain-like capabilities, as the highly complex heterarchical structure of the neural connections in the neocortex are potentially fundamental for its effectiveness. In this paper, we show how predictive coding (PC), a theory of information processing in the cortex, can be used to perform inference and learning on arbitrary graph topologies. We experimentally show how this formulation, called PC graphs, can be used to flexibly perform different tasks with the same network by simply stimulating specific neurons, and investigate how the topology of the graph influences the final performance. We conclude by comparing against simple baselines trained~with~BP.