AXIOM: Learning to Play Games in Minutes with Expanding Object-Centric Models

Current deep reinforcement learning (DRL) approaches achieve state-of-the-art performance in various domains, but struggle with data efficiency compared to human learning, which leverages core priors about objects and their interactions. Active inference offers a principled framework for integrating sensory information with prior knowledge to learn a world model and quantify the uncertainty of its own beliefs and predictions. However, active inference models are usually crafted for a single task with bespoke knowledge, so they lack the domain flexibility typical of DRL approaches. To bridge this gap, we propose a novel architecture that integrates a minimal yet expressive set of core priors about object-centric dynamics and interactions to accelerate learning in low-data regimes. The resulting approach, which we call AXIOM, combines the usual data efficiency and interpretability of Bayesian approaches with the across-task generalization usually associated with DRL. AXIOM represents scenes as compositions of objects, whose dynamics are modeled as piecewise linear trajectories that capture sparse object-object interactions. The structure of the generative model is expanded online by growing and learning mixture models from single events and periodically refined through Bayesian model reduction to induce generalization. AXIOM masters various games within only 10,000 interaction steps, with both a small number of parameters compared to DRL, and without the computational expense of gradient-based optimization.

Tight Stability, Convergence, and Robustness Bounds for Predictive Coding Networks

Energy-based learning algorithms, such as predictive coding (PC), have garnered significant attention in the machine learning community due to their theoretical properties, such as local operations and biologically plausible mechanisms for error correction. In this work, we rigorously analyze the stability, robustness, and convergence of PC through the lens of dynamical systems theory. We show that, first, PC is Lyapunov stable under mild assumptions on its loss and residual energy functions, which implies intrinsic robustness to small random perturbations due to its well-defined energy-minimizing dynamics. Second, we formally establish that the PC updates approximate quasi-Newton methods by incorporating higher-order curvature information, which makes them more stable and able to converge with fewer iterations compared to models trained via backpropagation (BP). Furthermore, using this dynamical framework, we provide new theoretical bounds on the similarity between PC and other algorithms, i.e., BP and target propagation (TP), by precisely characterizing the role of higher-order derivatives. These bounds, derived through detailed analysis of the Hessian structures, show that PC is significantly closer to quasi-Newton updates than TP, providing a deeper understanding of the stability and efficiency of PC compared to conventional learning methods.

Divide-and-Conquer Predictive Coding: a structured Bayesian inference algorithm

Unexpected stimuli induce "error" or "surprise" signals in the brain. The theory of predictive coding promises to explain these observations in terms of Bayesian inference by suggesting that the cortex implements variational inference in a probabilistic graphical model. However, when applied to machine learning tasks, this family of algorithms has yet to perform on par with other variational approaches in high-dimensional, structured inference problems. To address this, we introduce a novel predictive coding algorithm for structured generative models, that we call divide-and-conquer predictive coding (DCPC). DCPC differs from other formulations of predictive coding, as it respects the correlation structure of the generative model and provably performs maximum-likelihood updates of model parameters, all without sacrificing biological plausibility. Empirically, DCPC achieves better numerical performance than competing algorithms and provides accurate inference in a number of problems not previously addressed with predictive coding. We provide an open implementation of DCPC in Pyro on Github.

From pixels to planning: scale-free active inference

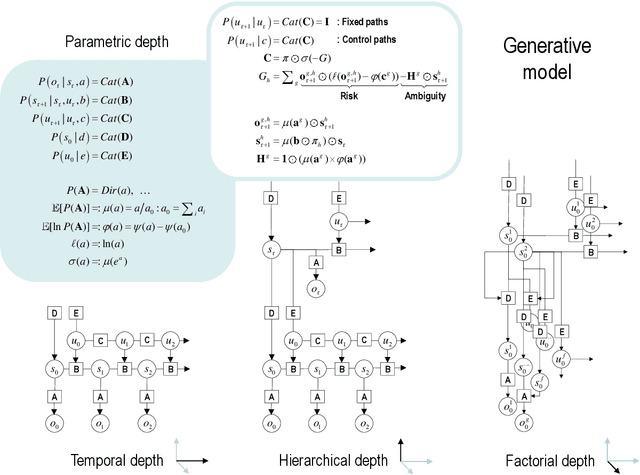
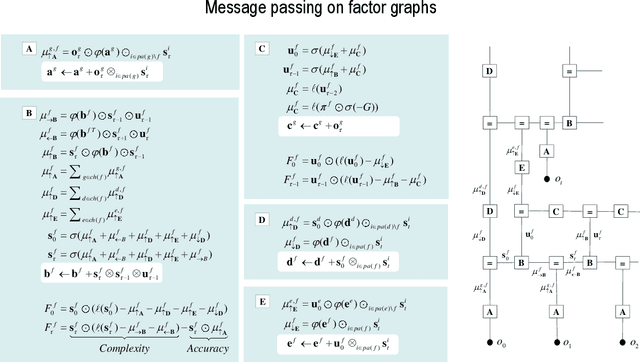
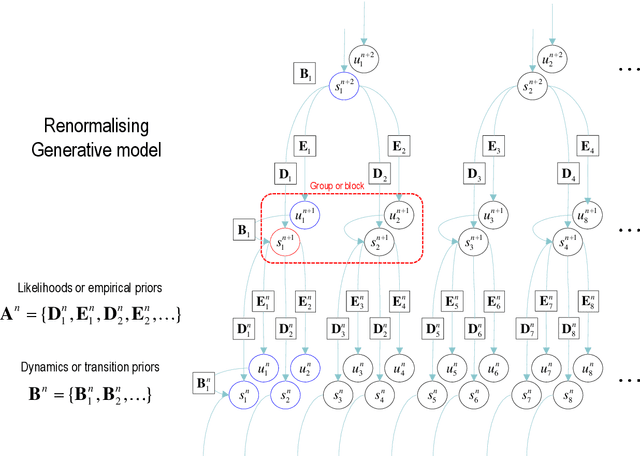
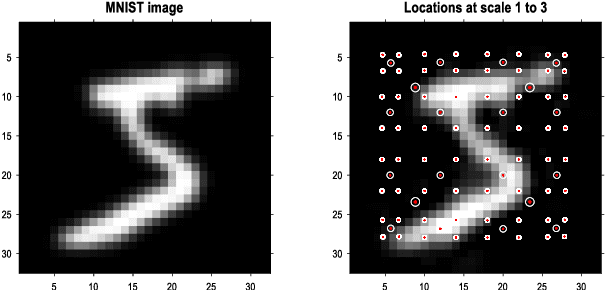
This paper describes a discrete state-space model -- and accompanying methods -- for generative modelling. This model generalises partially observed Markov decision processes to include paths as latent variables, rendering it suitable for active inference and learning in a dynamic setting. Specifically, we consider deep or hierarchical forms using the renormalisation group. The ensuing renormalising generative models (RGM) can be regarded as discrete homologues of deep convolutional neural networks or continuous state-space models in generalised coordinates of motion. By construction, these scale-invariant models can be used to learn compositionality over space and time, furnishing models of paths or orbits; i.e., events of increasing temporal depth and itinerancy. This technical note illustrates the automatic discovery, learning and deployment of RGMs using a series of applications. We start with image classification and then consider the compression and generation of movies and music. Finally, we apply the same variational principles to the learning of Atari-like games.

Benchmarking Predictive Coding Networks -- Made Simple

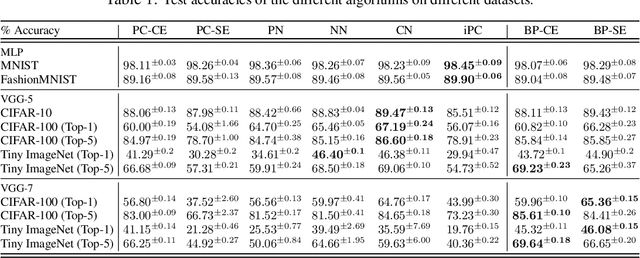
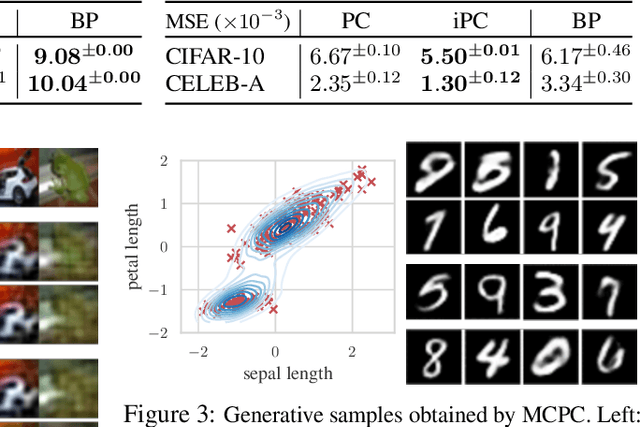
In this work, we tackle the problems of efficiency and scalability for predictive coding networks in machine learning. To do so, we first propose a library called PCX, whose focus lies on performance and simplicity, and provides a user-friendly, deep-learning oriented interface. Second, we use PCX to implement a large set of benchmarks for the community to use for their experiments. As most works propose their own tasks and architectures, do not compare one against each other, and focus on small-scale tasks, a simple and fast open-source library adopted by the whole community would address all of these concerns. Third, we perform extensive benchmarks using multiple algorithms, setting new state-of-the-art results in multiple tasks and datasets, as well as highlighting limitations inherent to PC that should be addressed. Thanks to the efficiency of PCX, we are able to analyze larger architectures than commonly used, providing baselines to galvanize community efforts towards one of the main open problems in the field: scalability. The code for PCX is available at \textit{https://github.com/liukidar/pcax}.

Associative Memories in the Feature Space

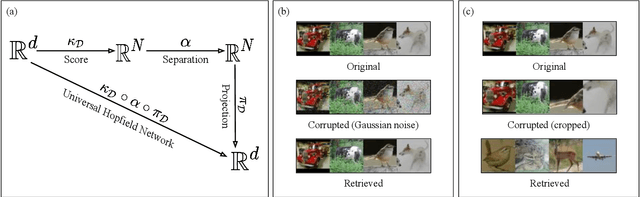
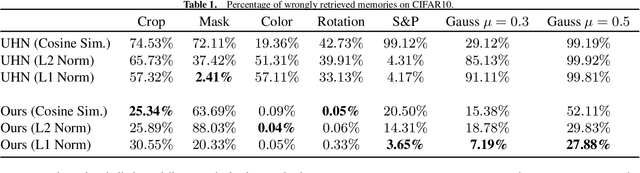
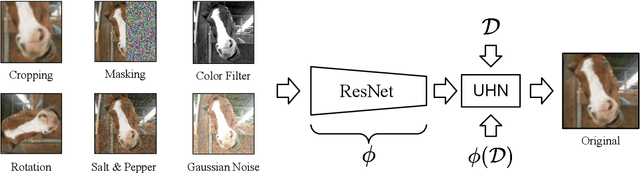
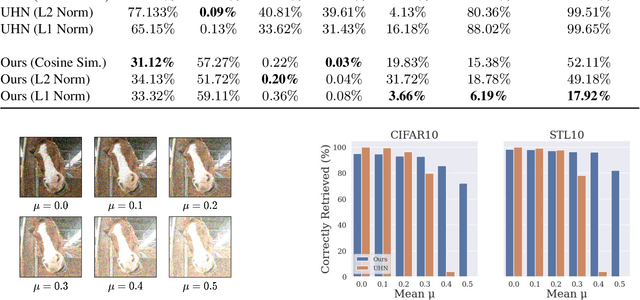
An autoassociative memory model is a function that, given a set of data points, takes as input an arbitrary vector and outputs the most similar data point from the memorized set. However, popular memory models fail to retrieve images even when the corruption is mild and easy to detect for a human evaluator. This is because similarities are evaluated in the raw pixel space, which does not contain any semantic information about the images. This problem can be easily solved by computing \emph{similarities} in an embedding space instead of the pixel space. We show that an effective way of computing such embeddings is via a network pretrained with a contrastive loss. As the dimension of embedding spaces is often significantly smaller than the pixel space, we also have a faster computation of similarity scores. We test this method on complex datasets such as CIFAR10 and STL10. An additional drawback of current models is the need of storing the whole dataset in the pixel space, which is often extremely large. We relax this condition and propose a class of memory models that only stores low-dimensional semantic embeddings, and uses them to retrieve similar, but not identical, memories. We demonstrate a proof of concept of this method on a simple task on the MNIST dataset.

Active Inference and Intentional Behaviour

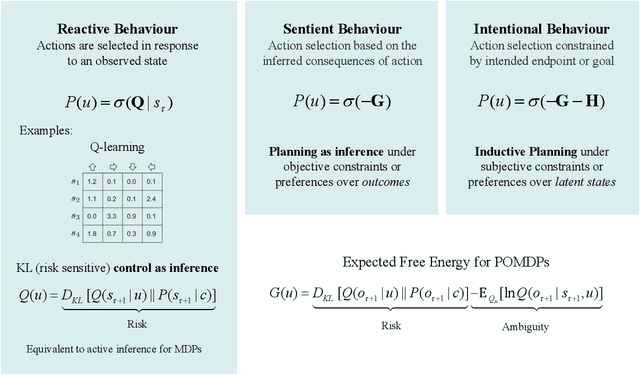
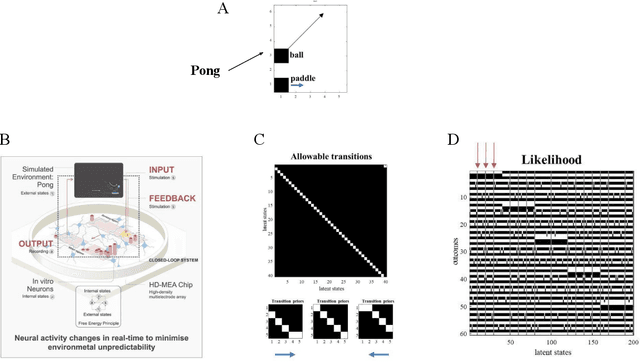
Recent advances in theoretical biology suggest that basal cognition and sentient behaviour are emergent properties of in vitro cell cultures and neuronal networks, respectively. Such neuronal networks spontaneously learn structured behaviours in the absence of reward or reinforcement. In this paper, we characterise this kind of self-organisation through the lens of the free energy principle, i.e., as self-evidencing. We do this by first discussing the definitions of reactive and sentient behaviour in the setting of active inference, which describes the behaviour of agents that model the consequences of their actions. We then introduce a formal account of intentional behaviour, that describes agents as driven by a preferred endpoint or goal in latent state-spaces. We then investigate these forms of (reactive, sentient, and intentional) behaviour using simulations. First, we simulate the aforementioned in vitro experiments, in which neuronal cultures spontaneously learn to play Pong, by implementing nested, free energy minimising processes. The simulations are then used to deconstruct the ensuing predictive behaviour, leading to the distinction between merely reactive, sentient, and intentional behaviour, with the latter formalised in terms of inductive planning. This distinction is further studied using simple machine learning benchmarks (navigation in a grid world and the Tower of Hanoi problem), that show how quickly and efficiently adaptive behaviour emerges under an inductive form of active inference.

Supervised structure learning

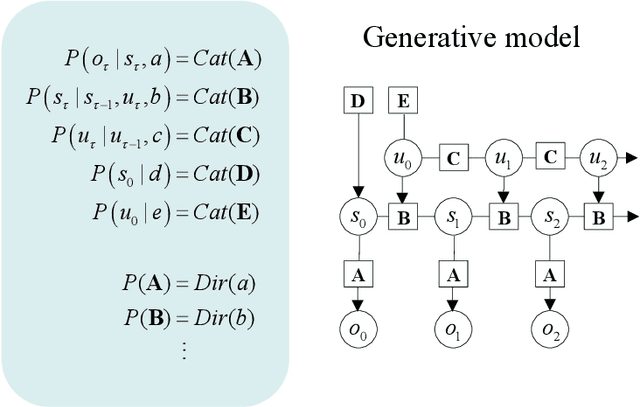
This paper concerns structure learning or discovery of discrete generative models. It focuses on Bayesian model selection and the assimilation of training data or content, with a special emphasis on the order in which data are ingested. A key move - in the ensuing schemes - is to place priors on the selection of models, based upon expected free energy. In this setting, expected free energy reduces to a constrained mutual information, where the constraints inherit from priors over outcomes (i.e., preferred outcomes). The resulting scheme is first used to perform image classification on the MNIST dataset to illustrate the basic idea, and then tested on a more challenging problem of discovering models with dynamics, using a simple sprite-based visual disentanglement paradigm and the Tower of Hanoi (cf., blocks world) problem. In these examples, generative models are constructed autodidactically to recover (i.e., disentangle) the factorial structure of latent states - and their characteristic paths or dynamics.

Brain-Inspired Computational Intelligence via Predictive Coding

Artificial intelligence (AI) is rapidly becoming one of the key technologies of this century. The majority of results in AI thus far have been achieved using deep neural networks trained with the error backpropagation learning algorithm. However, the ubiquitous adoption of this approach has highlighted some important limitations such as substantial computational cost, difficulty in quantifying uncertainty, lack of robustness, unreliability, and biological implausibility. It is possible that addressing these limitations may require schemes that are inspired and guided by neuroscience theories. One such theory, called predictive coding (PC), has shown promising performance in machine intelligence tasks, exhibiting exciting properties that make it potentially valuable for the machine learning community: PC can model information processing in different brain areas, can be used in cognitive control and robotics, and has a solid mathematical grounding in variational inference, offering a powerful inversion scheme for a specific class of continuous-state generative models. With the hope of foregrounding research in this direction, we survey the literature that has contributed to this perspective, highlighting the many ways that PC might play a role in the future of machine learning and computational intelligence at large.

Causal Inference via Predictive Coding

Bayesian and causal inference are fundamental processes for intelligence. Bayesian inference models observations: what can be inferred about y if we observe a related variable x? Causal inference models interventions: if we directly change x, how will y change? Predictive coding is a neuroscience-inspired method for performing Bayesian inference on continuous state variables using local information only. In this work, we go beyond Bayesian inference, and show how a simple change in the inference process of predictive coding enables interventional and counterfactual inference in scenarios where the causal graph is known. We then extend our results, and show how predictive coding can be generalized to cases where this graph is unknown, and has to be inferred from data, hence performing causal discovery. What results is a novel and straightforward technique that allows us to perform end-to-end causal inference on predictive-coding-based structural causal models, and demonstrate its utility for potential applications in machine learning.