Active inference and artificial reasoning

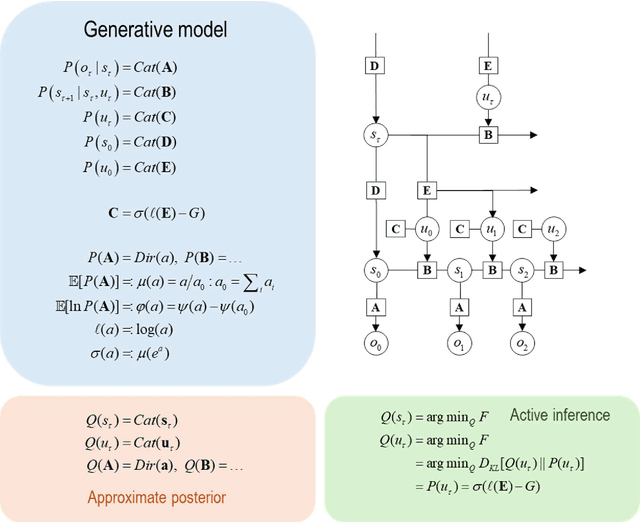
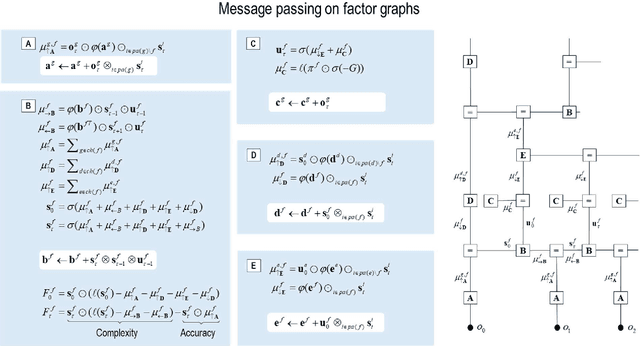
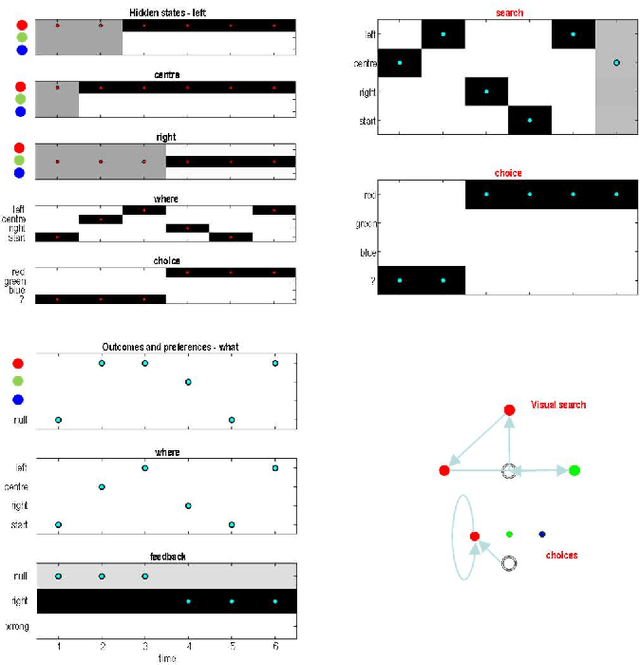
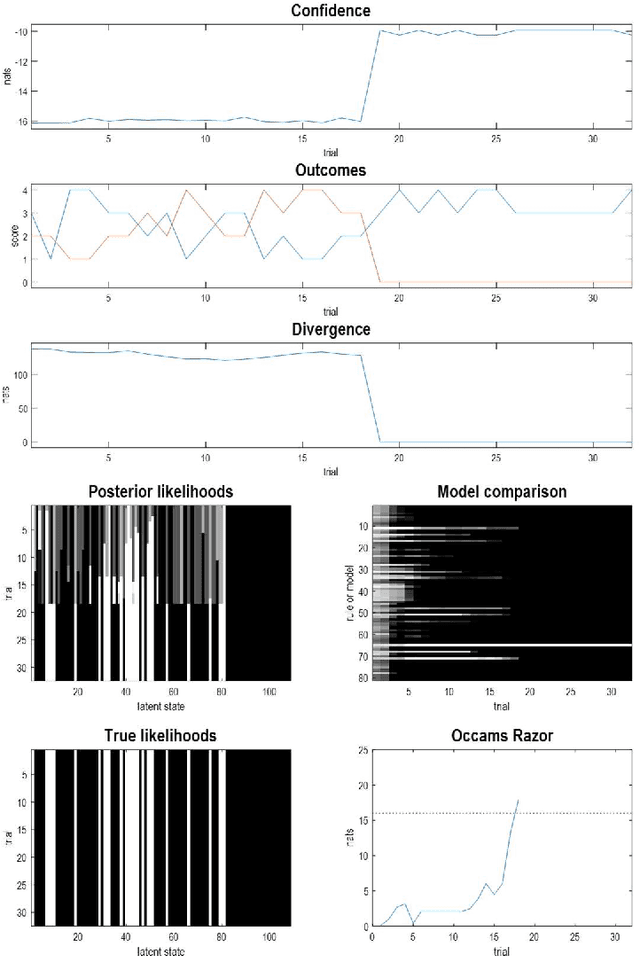
This technical note considers the sampling of outcomes that provide the greatest amount of information about the structure of underlying world models. This generalisation furnishes a principled approach to structure learning under a plausible set of generative models or hypotheses. In active inference, policies - i.e., combinations of actions - are selected based on their expected free energy, which comprises expected information gain and value. Information gain corresponds to the KL divergence between predictive posteriors with, and without, the consequences of action. Posteriors over models can be evaluated quickly and efficiently using Bayesian Model Reduction, based upon accumulated posterior beliefs about model parameters. The ensuing information gain can then be used to select actions that disambiguate among alternative models, in the spirit of optimal experimental design. We illustrate this kind of active selection or reasoning using partially observed discrete models; namely, a 'three-ball' paradigm used previously to describe artificial insight and 'aha moments' via (synthetic) introspection or sleep. We focus on the sample efficiency afforded by seeking outcomes that resolve the greatest uncertainty about the world model, under which outcomes are generated.

Bayesian Predictive Coding

Predictive coding (PC) is an influential theory of information processing in the brain, providing a biologically plausible alternative to backpropagation. It is motivated in terms of Bayesian inference, as hidden states and parameters are optimised via gradient descent on variational free energy. However, implementations of PC rely on maximum \textit{a posteriori} (MAP) estimates of hidden states and maximum likelihood (ML) estimates of parameters, limiting their ability to quantify epistemic uncertainty. In this work, we investigate a Bayesian extension to PC that estimates a posterior distribution over network parameters. This approach, termed Bayesian Predictive coding (BPC), preserves the locality of PC and results in closed-form Hebbian weight updates. Compared to PC, our BPC algorithm converges in fewer epochs in the full-batch setting and remains competitive in the mini-batch setting. Additionally, we demonstrate that BPC offers uncertainty quantification comparable to existing methods in Bayesian deep learning, while also improving convergence properties. Together, these results suggest that BPC provides a biologically plausible method for Bayesian learning in the brain, as well as an attractive approach to uncertainty quantification in deep learning.

Toward Universal and Interpretable World Models for Open-ended Learning Agents

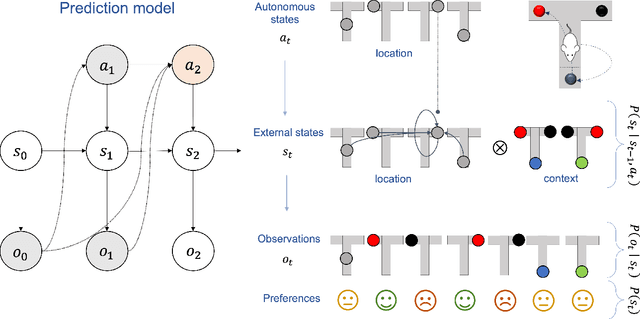
We introduce a generic, compositional and interpretable class of generative world models that supports open-ended learning agents. This is a sparse class of Bayesian networks capable of approximating a broad range of stochastic processes, which provide agents with the ability to learn world models in a manner that may be both interpretable and computationally scalable. This approach integrating Bayesian structure learning and intrinsically motivated (model-based) planning enables agents to actively develop and refine their world models, which may lead to open-ended learning and more robust, adaptive behavior.

From pixels to planning: scale-free active inference

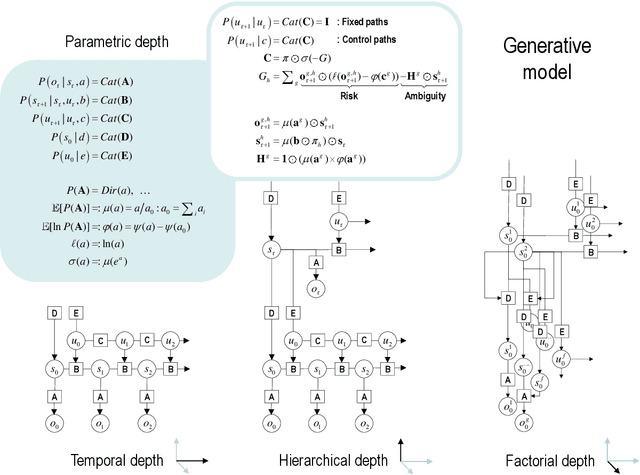
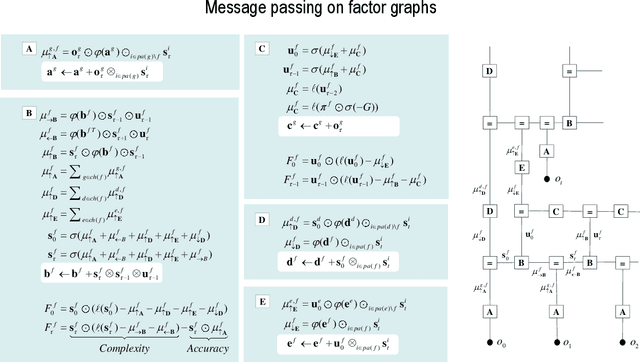
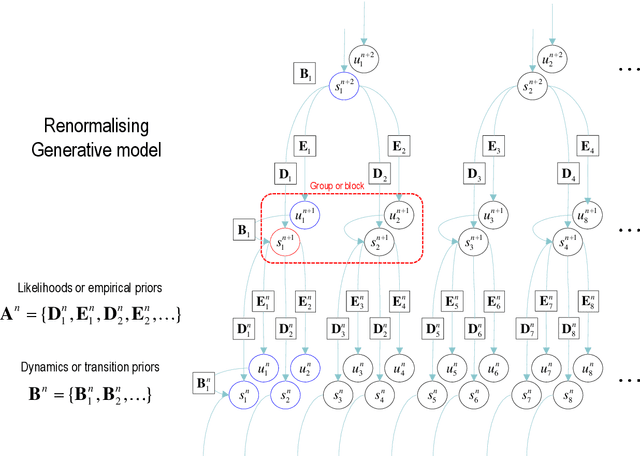
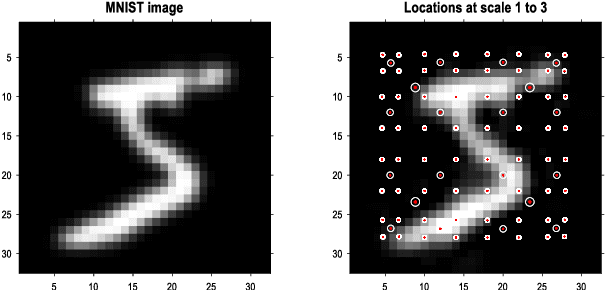
This paper describes a discrete state-space model -- and accompanying methods -- for generative modelling. This model generalises partially observed Markov decision processes to include paths as latent variables, rendering it suitable for active inference and learning in a dynamic setting. Specifically, we consider deep or hierarchical forms using the renormalisation group. The ensuing renormalising generative models (RGM) can be regarded as discrete homologues of deep convolutional neural networks or continuous state-space models in generalised coordinates of motion. By construction, these scale-invariant models can be used to learn compositionality over space and time, furnishing models of paths or orbits; i.e., events of increasing temporal depth and itinerancy. This technical note illustrates the automatic discovery, learning and deployment of RGMs using a series of applications. We start with image classification and then consider the compression and generation of movies and music. Finally, we apply the same variational principles to the learning of Atari-like games.

Active Inference as a Model of Agency

Is there a canonical way to think of agency beyond reward maximisation? In this paper, we show that any type of behaviour complying with physically sound assumptions about how macroscopic biological agents interact with the world canonically integrates exploration and exploitation in the sense of minimising risk and ambiguity about states of the world. This description, known as active inference, refines the free energy principle, a popular descriptive framework for action and perception originating in neuroscience. Active inference provides a normative Bayesian framework to simulate and model agency that is widely used in behavioural neuroscience, reinforcement learning (RL) and robotics. The usefulness of active inference for RL is three-fold. \emph{a}) Active inference provides a principled solution to the exploration-exploitation dilemma that usefully simulates biological agency. \emph{b}) It provides an explainable recipe to simulate behaviour, whence behaviour follows as an explainable mixture of exploration and exploitation under a generative world model, and all differences in behaviour are explicit in differences in world model. \emph{c}) This framework is universal in the sense that it is theoretically possible to rewrite any RL algorithm conforming to the descriptive assumptions of active inference as an active inference algorithm. Thus, active inference can be used as a tool to uncover and compare the commitments and assumptions of more specific models of agency.

Sample Path Regularity of Gaussian Processes from the Covariance Kernel

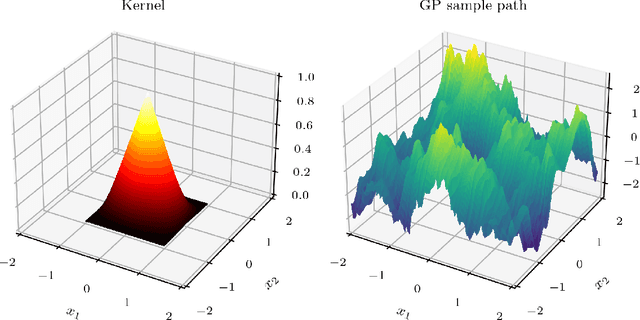
Gaussian processes (GPs) are the most common formalism for defining probability distributions over spaces of functions. While applications of GPs are myriad, a comprehensive understanding of GP sample paths, i.e. the function spaces over which they define a probability measure on, is lacking. In practice, GPs are not constructed through a probability measure, but instead through a mean function and a covariance kernel. In this paper we provide necessary and sufficient conditions on the covariance kernel for the sample paths of the corresponding GP to attain a given regularity. We use the framework of H\"older regularity as it grants us particularly straightforward conditions, which simplify further in the cases of stationary and isotropic GPs. We then demonstrate that our results allow for novel and unusually tight characterisations of the sample path regularities of the GPs commonly used in machine learning applications, such as the Mat\'ern GPs.

Supervised structure learning

This paper concerns structure learning or discovery of discrete generative models. It focuses on Bayesian model selection and the assimilation of training data or content, with a special emphasis on the order in which data are ingested. A key move - in the ensuing schemes - is to place priors on the selection of models, based upon expected free energy. In this setting, expected free energy reduces to a constrained mutual information, where the constraints inherit from priors over outcomes (i.e., preferred outcomes). The resulting scheme is first used to perform image classification on the MNIST dataset to illustrate the basic idea, and then tested on a more challenging problem of discovering models with dynamics, using a simple sprite-based visual disentanglement paradigm and the Tower of Hanoi (cf., blocks world) problem. In these examples, generative models are constructed autodidactically to recover (i.e., disentangle) the factorial structure of latent states - and their characteristic paths or dynamics.

On efficient computation in active inference

Despite being recognized as neurobiologically plausible, active inference faces difficulties when employed to simulate intelligent behaviour in complex environments due to its computational cost and the difficulty of specifying an appropriate target distribution for the agent. This paper introduces two solutions that work in concert to address these limitations. First, we present a novel planning algorithm for finite temporal horizons with drastically lower computational complexity. Second, inspired by Z-learning from control theory literature, we simplify the process of setting an appropriate target distribution for new and existing active inference planning schemes. Our first approach leverages the dynamic programming algorithm, known for its computational efficiency, to minimize the cost function used in planning through the Bellman-optimality principle. Accordingly, our algorithm recursively assesses the expected free energy of actions in the reverse temporal order. This improves computational efficiency by orders of magnitude and allows precise model learning and planning, even under uncertain conditions. Our method simplifies the planning process and shows meaningful behaviour even when specifying only the agent's final goal state. The proposed solutions make defining a target distribution from a goal state straightforward compared to the more complicated task of defining a temporally informed target distribution. The effectiveness of these methods is tested and demonstrated through simulations in standard grid-world tasks. These advances create new opportunities for various applications.

Modelling non-reinforced preferences using selective attention

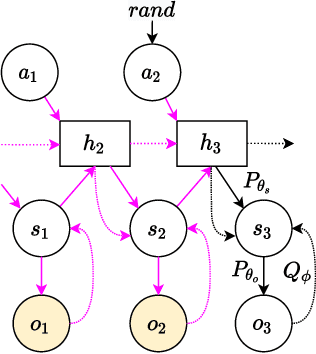
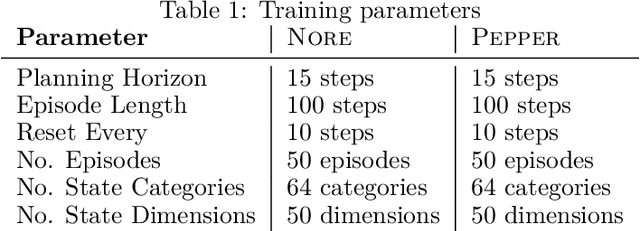
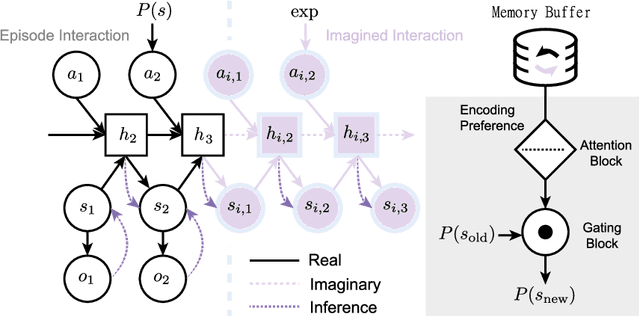
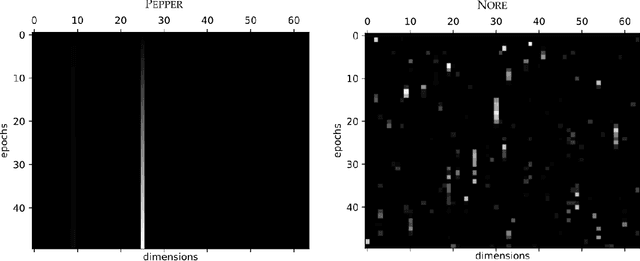
How can artificial agents learn non-reinforced preferences to continuously adapt their behaviour to a changing environment? We decompose this question into two challenges: ($i$) encoding diverse memories and ($ii$) selectively attending to these for preference formation. Our proposed \emph{no}n-\emph{re}inforced preference learning mechanism using selective attention, \textsc{Nore}, addresses both by leveraging the agent's world model to collect a diverse set of experiences which are interleaved with imagined roll-outs to encode memories. These memories are selectively attended to, using attention and gating blocks, to update agent's preferences. We validate \textsc{Nore} in a modified OpenAI Gym FrozenLake environment (without any external signal) with and without volatility under a fixed model of the environment -- and compare its behaviour to \textsc{Pepper}, a Hebbian preference learning mechanism. We demonstrate that \textsc{Nore} provides a straightforward framework to induce exploratory preferences in the absence of external signals.

Geometric Methods for Sampling, Optimisation, Inference and Adaptive Agents

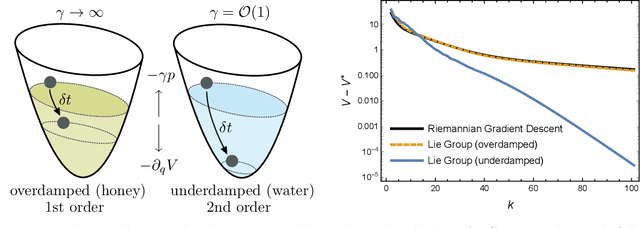
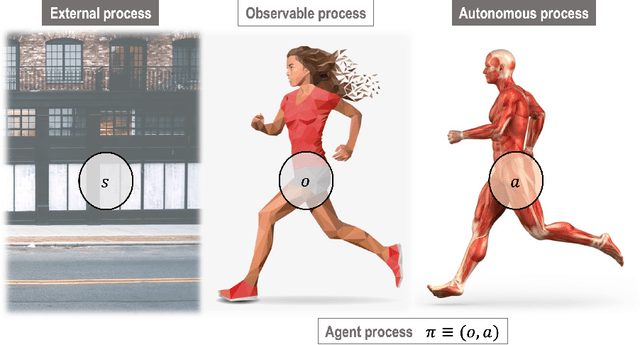
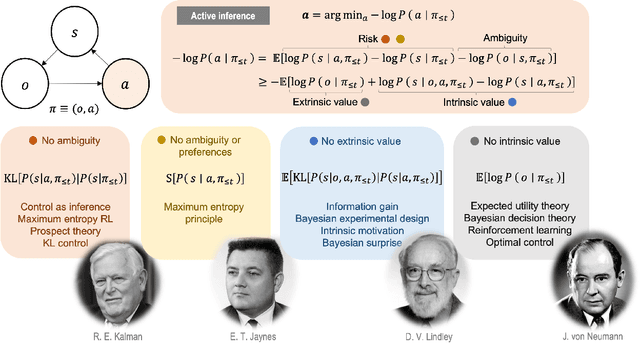
In this chapter, we identify fundamental geometric structures that underlie the problems of sampling, optimisation, inference and adaptive decision-making. Based on this identification, we derive algorithms that exploit these geometric structures to solve these problems efficiently. We show that a wide range of geometric theories emerge naturally in these fields, ranging from measure-preserving processes, information divergences, Poisson geometry, and geometric integration. Specifically, we explain how \emph{(i)} leveraging the symplectic geometry of Hamiltonian systems enable us to construct (accelerated) sampling and optimisation methods, \emph{(ii)} the theory of Hilbertian subspaces and Stein operators provides a general methodology to obtain robust estimators, \emph{(iii)} preserving the information geometry of decision-making yields adaptive agents that perform active inference. Throughout, we emphasise the rich connections between these fields; e.g., inference draws on sampling and optimisation, and adaptive decision-making assesses decisions by inferring their counterfactual consequences. Our exposition provides a conceptual overview of underlying ideas, rather than a technical discussion, which can be found in the references herein.