Neural parameter calibration and uncertainty quantification for epidemic forecasting

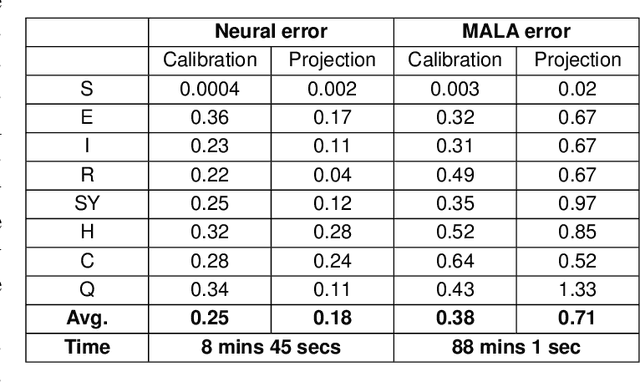
The recent COVID-19 pandemic has thrown the importance of accurately forecasting contagion dynamics and learning infection parameters into sharp focus. At the same time, effective policy-making requires knowledge of the uncertainty on such predictions, in order, for instance, to be able to ready hospitals and intensive care units for a worst-case scenario without needlessly wasting resources. In this work, we apply a novel and powerful computational method to the problem of learning probability densities on contagion parameters and providing uncertainty quantification for pandemic projections. Using a neural network, we calibrate an ODE model to data of the spread of COVID-19 in Berlin in 2020, achieving both a significantly more accurate calibration and prediction than Markov-Chain Monte Carlo (MCMC)-based sampling schemes. The uncertainties on our predictions provide meaningful confidence intervals e.g. on infection figures and hospitalisation rates, while training and running the neural scheme takes minutes where MCMC takes hours. We show convergence of our method to the true posterior on a simplified SIR model of epidemics, and also demonstrate our method's learning capabilities on a reduced dataset, where a complex model is learned from a small number of compartments for which data is available.

Machine Learning for the identification of phase-transitions in interacting agent-based systems

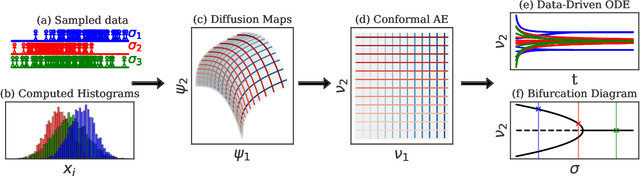
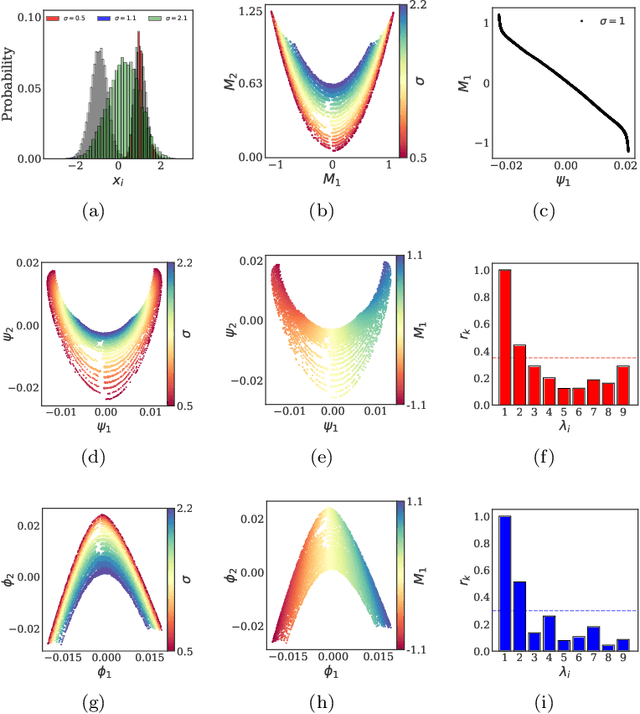
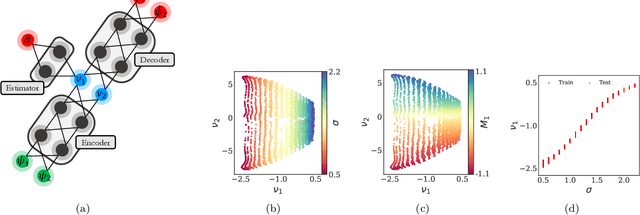
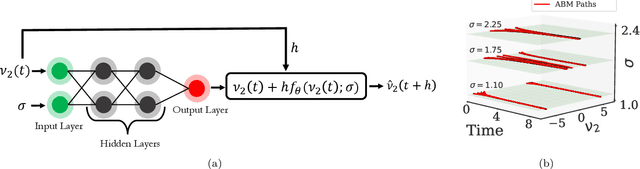
Deriving closed-form, analytical expressions for reduced-order models, and judiciously choosing the closures leading to them, has long been the strategy of choice for studying phase- and noise-induced transitions for agent-based models (ABMs). In this paper, we propose a data-driven framework that pinpoints phase transitions for an ABM in its mean-field limit, using a smaller number of variables than traditional closed-form models. To this end, we use the manifold learning algorithm Diffusion Maps to identify a parsimonious set of data-driven latent variables, and show that they are in one-to-one correspondence with the expected theoretical order parameter of the ABM. We then utilize a deep learning framework to obtain a conformal reparametrization of the data-driven coordinates that facilitates, in our example, the identification of a single parameter-dependent ODE in these coordinates. We identify this ODE through a residual neural network inspired by a numerical integration scheme (forward Euler). We then use the identified ODE -- enabled through an odd symmetry transformation -- to construct the bifurcation diagram exhibiting the phase transition.

Inferring networks from time series: a neural approach

Network structures underlie the dynamics of many complex phenomena, from gene regulation and foodwebs to power grids and social media. Yet, as they often cannot be observed directly, their connectivities must be inferred from observations of their emergent dynamics. In this work we present a powerful and fast computational method to infer large network adjacency matrices from time series data using a neural network. Using a neural network provides uncertainty quantification on the prediction in a manner that reflects both the non-convexity of the inference problem as well as the noise on the data. This is useful since network inference problems are typically underdetermined, and a feature that has hitherto been lacking from network inference methods. We demonstrate our method's capabilities by inferring line failure locations in the British power grid from observations of its response to a power cut. Since the problem is underdetermined, many classical statistical tools (e.g. regression) will not be straightforwardly applicable. Our method, in contrast, provides probability densities on each edge, allowing the use of hypothesis testing to make meaningful probabilistic statements about the location of the power cut. We also demonstrate our method's ability to learn an entire cost matrix for a non-linear model from a dataset of economic activity in Greater London. Our method outperforms OLS regression on noisy data in terms of both speed and prediction accuracy, and scales as $N^2$ where OLS is cubic. Since our technique is not specifically engineered for network inference, it represents a general parameter estimation scheme that is applicable to any parameter dimension.

Neural parameter calibration for large-scale multi-agent models

Computational models have become a powerful tool in the quantitative sciences to understand the behaviour of complex systems that evolve in time. However, they often contain a potentially large number of free parameters whose values cannot be obtained from theory but need to be inferred from data. This is especially the case for models in the social sciences, economics, or computational epidemiology. Yet many current parameter estimation methods are mathematically involved and computationally slow to run. In this paper we present a computationally simple and fast method to retrieve accurate probability densities for model parameters using neural differential equations. We present a pipeline comprising multi-agent models acting as forward solvers for systems of ordinary or stochastic differential equations, and a neural network to then extract parameters from the data generated by the model. The two combined create a powerful tool that can quickly estimate densities on model parameters, even for very large systems. We demonstrate the method on synthetic time series data of the SIR model of the spread of infection, and perform an in-depth analysis of the Harris-Wilson model of economic activity on a network, representing a non-convex problem. For the latter, we apply our method both to synthetic data and to data of economic activity across Greater London. We find that our method calibrates the model orders of magnitude more accurately than a previous study of the same dataset using classical techniques, while running between 195 and 390 times faster.

Geometric Methods for Sampling, Optimisation, Inference and Adaptive Agents

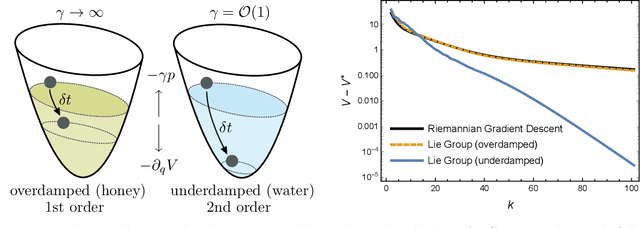
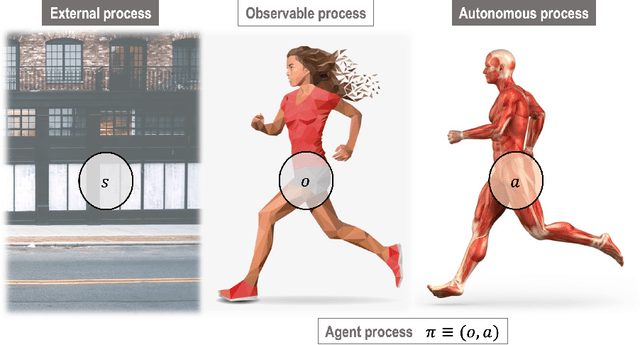
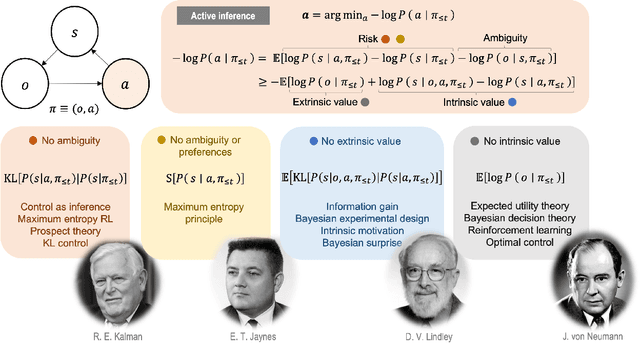
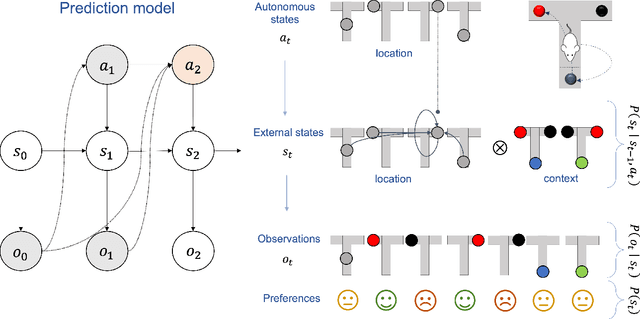
In this chapter, we identify fundamental geometric structures that underlie the problems of sampling, optimisation, inference and adaptive decision-making. Based on this identification, we derive algorithms that exploit these geometric structures to solve these problems efficiently. We show that a wide range of geometric theories emerge naturally in these fields, ranging from measure-preserving processes, information divergences, Poisson geometry, and geometric integration. Specifically, we explain how \emph{(i)} leveraging the symplectic geometry of Hamiltonian systems enable us to construct (accelerated) sampling and optimisation methods, \emph{(ii)} the theory of Hilbertian subspaces and Stein operators provides a general methodology to obtain robust estimators, \emph{(iii)} preserving the information geometry of decision-making yields adaptive agents that perform active inference. Throughout, we emphasise the rich connections between these fields; e.g., inference draws on sampling and optimisation, and adaptive decision-making assesses decisions by inferring their counterfactual consequences. Our exposition provides a conceptual overview of underlying ideas, rather than a technical discussion, which can be found in the references herein.

On stochastic mirror descent with interacting particles: convergence properties and variance reduction

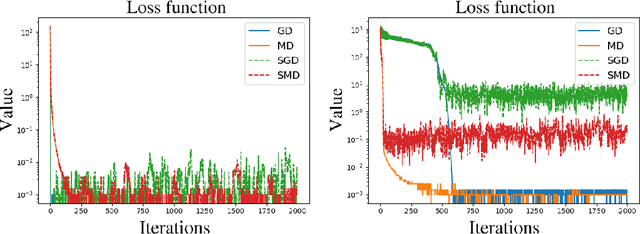
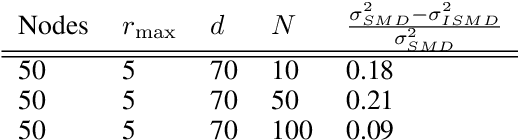
An open problem in optimization with noisy information is the computation of an exact minimizer that is independent of the amount of noise. A standard practice in stochastic approximation algorithms is to use a decreasing step-size. However, to converge the step-size must decrease exponentially slow, and therefore this approach is not useful in practice. A second alternative is to use a fixed step-size and run independent replicas of the algorithm and average these. A third option is to run replicas of the algorithm and allow them to interact. It is unclear which of these options works best. To address this question, we reduce the problem of the computation of an exact minimizer with noisy gradient information to the study of stochastic mirror descent with interacting particles. We study the convergence of stochastic mirror descent and make explicit the tradeoffs between communication and variance reduction. We provide theoretical and numerical evidence to suggest that interaction helps to improve convergence and reduce the variance of the estimate.

The sharp, the flat and the shallow: Can weakly interacting agents learn to escape bad minima?

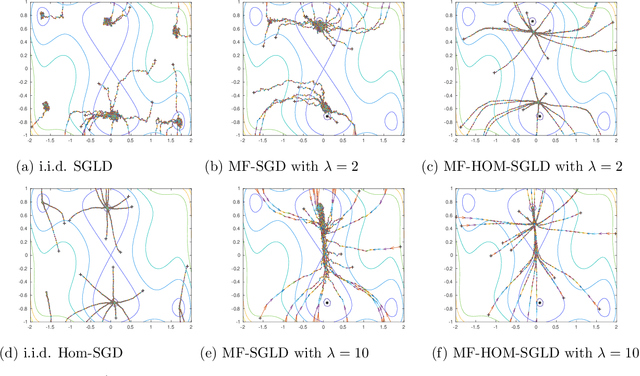
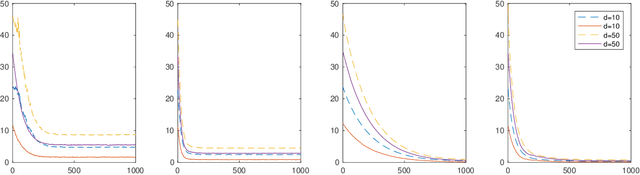
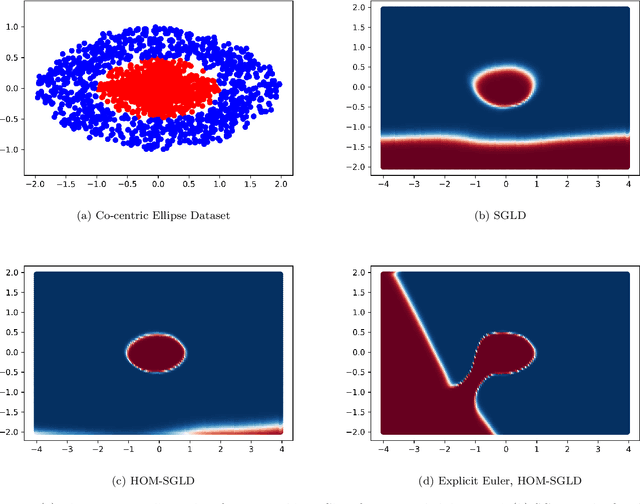
An open problem in machine learning is whether flat minima generalize better and how to compute such minima efficiently. This is a very challenging problem. As a first step towards understanding this question we formalize it as an optimization problem with weakly interacting agents. We review appropriate background material from the theory of stochastic processes and provide insights that are relevant to practitioners. We propose an algorithmic framework for an extended stochastic gradient Langevin dynamics and illustrate its potential. The paper is written as a tutorial, and presents an alternative use of multi-agent learning. Our primary focus is on the design of algorithms for machine learning applications; however the underlying mathematical framework is suitable for the understanding of large scale systems of agent based models that are popular in the social sciences, economics and finance.