Neural parameter calibration and uncertainty quantification for epidemic forecasting
Paper and Code
Dec 05, 2023


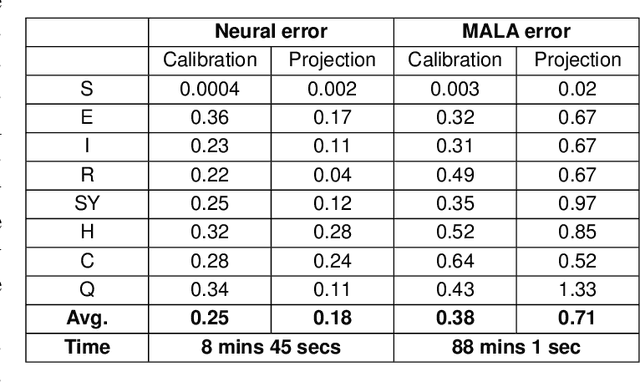
The recent COVID-19 pandemic has thrown the importance of accurately forecasting contagion dynamics and learning infection parameters into sharp focus. At the same time, effective policy-making requires knowledge of the uncertainty on such predictions, in order, for instance, to be able to ready hospitals and intensive care units for a worst-case scenario without needlessly wasting resources. In this work, we apply a novel and powerful computational method to the problem of learning probability densities on contagion parameters and providing uncertainty quantification for pandemic projections. Using a neural network, we calibrate an ODE model to data of the spread of COVID-19 in Berlin in 2020, achieving both a significantly more accurate calibration and prediction than Markov-Chain Monte Carlo (MCMC)-based sampling schemes. The uncertainties on our predictions provide meaningful confidence intervals e.g. on infection figures and hospitalisation rates, while training and running the neural scheme takes minutes where MCMC takes hours. We show convergence of our method to the true posterior on a simplified SIR model of epidemics, and also demonstrate our method's learning capabilities on a reduced dataset, where a complex model is learned from a small number of compartments for which data is available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge