Christof Schütte
Generative modeling of conditional probability distributions on the level-sets of collective variables
Dec 22, 2025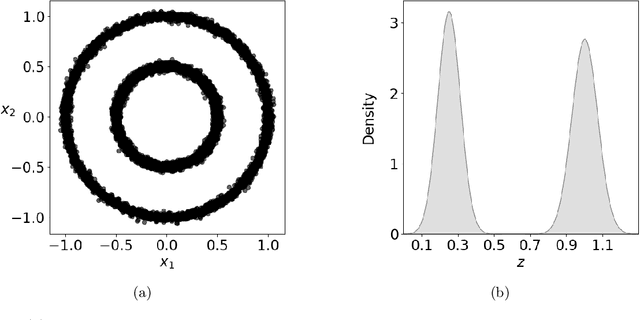
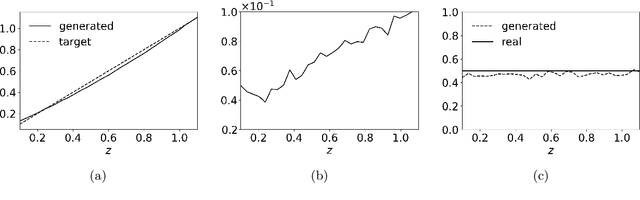

Abstract:Given a probability distribution $μ$ in $\mathbb{R}^d$ represented by data, we study in this paper the generative modeling of its conditional probability distributions on the level-sets of a collective variable $ξ: \mathbb{R}^d \rightarrow \mathbb{R}^k$, where $1 \le k<d$. We propose a general and efficient learning approach that is able to learn generative models on different level-sets of $ξ$ simultaneously. To improve the learning quality on level-sets in low-probability regions, we also propose a strategy for data enrichment by utilizing data from enhanced sampling techniques. We demonstrate the effectiveness of our proposed learning approach through concrete numerical examples. The proposed approach is potentially useful for the generative modeling of molecular systems in biophysics, for instance.
Riemannian Denoising Diffusion Probabilistic Models
May 07, 2025Abstract:We propose Riemannian Denoising Diffusion Probabilistic Models (RDDPMs) for learning distributions on submanifolds of Euclidean space that are level sets of functions, including most of the manifolds relevant to applications. Existing methods for generative modeling on manifolds rely on substantial geometric information such as geodesic curves or eigenfunctions of the Laplace-Beltrami operator and, as a result, they are limited to manifolds where such information is available. In contrast, our method, built on a projection scheme, can be applied to more general manifolds, as it only requires being able to evaluate the value and the first order derivatives of the function that defines the submanifold. We provide a theoretical analysis of our method in the continuous-time limit, which elucidates the connection between our RDDPMs and score-based generative models on manifolds. The capability of our method is demonstrated on datasets from previous studies and on new datasets sampled from two high-dimensional manifolds, i.e. $\mathrm{SO}(10)$ and the configuration space of molecular system alanine dipeptide with fixed dihedral angle.
Neural parameter calibration and uncertainty quantification for epidemic forecasting
Dec 05, 2023


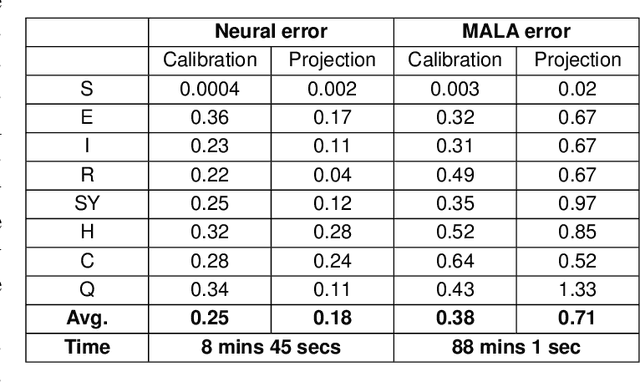
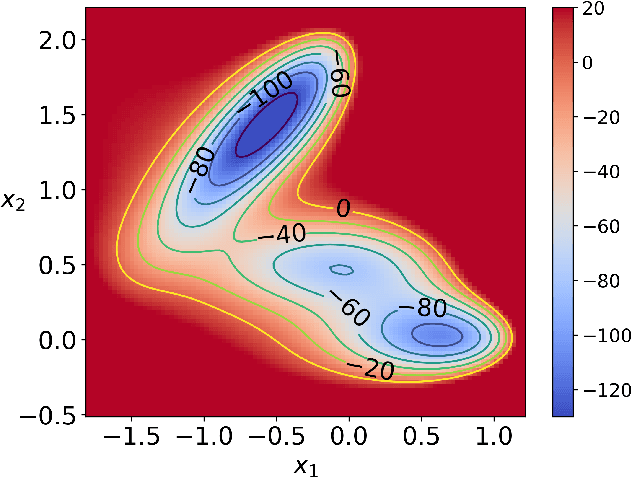
Abstract:The recent COVID-19 pandemic has thrown the importance of accurately forecasting contagion dynamics and learning infection parameters into sharp focus. At the same time, effective policy-making requires knowledge of the uncertainty on such predictions, in order, for instance, to be able to ready hospitals and intensive care units for a worst-case scenario without needlessly wasting resources. In this work, we apply a novel and powerful computational method to the problem of learning probability densities on contagion parameters and providing uncertainty quantification for pandemic projections. Using a neural network, we calibrate an ODE model to data of the spread of COVID-19 in Berlin in 2020, achieving both a significantly more accurate calibration and prediction than Markov-Chain Monte Carlo (MCMC)-based sampling schemes. The uncertainties on our predictions provide meaningful confidence intervals e.g. on infection figures and hospitalisation rates, while training and running the neural scheme takes minutes where MCMC takes hours. We show convergence of our method to the true posterior on a simplified SIR model of epidemics, and also demonstrate our method's learning capabilities on a reduced dataset, where a complex model is learned from a small number of compartments for which data is available.
Understanding recent deep-learning techniques for identifying collective variables of molecular dynamics
Jul 01, 2023Abstract:The dynamics of a high-dimensional metastable molecular system can often be characterised by a few features of the system, i.e. collective variables (CVs). Thanks to the rapid advance in the area of machine learning, various deep learning-based CV identification techniques have been developed in recent years, allowing accurate modelling and efficient simulation of complex molecular systems. In this paper, we look at two different categories of deep learning-based approaches for finding CVs, either by computing leading eigenfunctions of infinitesimal generator or transfer operator associated to the underlying dynamics, or by learning an autoencoder via minimisation of reconstruction error. We present a concise overview of the mathematics behind these two approaches and conduct a comparative numerical study of these two approaches on illustrative examples.
Impact Study of Numerical Discretization Accuracy on Parameter Reconstructions and Model Parameter Distributions
May 04, 2023Abstract:Numerical models are used widely for parameter reconstructions in the field of optical nano metrology. To obtain geometrical parameters of a nano structured line grating, we fit a finite element numerical model to an experimental data set by using the Bayesian target vector optimization method. Gaussian process surrogate models are trained during the reconstruction. Afterwards, we employ a Markov chain Monte Carlo sampler on the surrogate models to determine the full model parameter distribution for the reconstructed model parameters. The choice of numerical discretization parameters, like the polynomial order of the finite element ansatz functions, impacts the numerical discretization error of the forward model. In this study we investigate the impact of numerical discretization parameters of the forward problem on the reconstructed parameters as well as on the model parameter distributions. We show that such a convergence study allows to determine numerical parameters which allow for efficient and accurate reconstruction results.
Data-driven modelling of nonlinear dynamics by polytope projections and memory
Dec 13, 2021
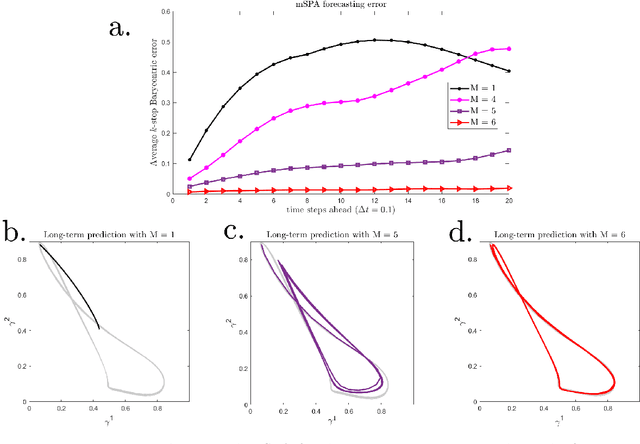


Abstract:We present a numerical method to model dynamical systems from data. We use the recently introduced method Scalable Probabilistic Approximation (SPA) to project points from a Euclidean space to convex polytopes and represent these projected states of a system in new, lower-dimensional coordinates denoting their position in the polytope. We then introduce a specific nonlinear transformation to construct a model of the dynamics in the polytope and to transform back into the original state space. To overcome the potential loss of information from the projection to a lower-dimensional polytope, we use memory in the sense of the delay-embedding theorem of Takens. By construction, our method produces stable models. We illustrate the capacity of the method to reproduce even chaotic dynamics and attractors with multiple connected components on various examples.
Data-driven model reduction of agent-based systems using the Koopman generator
Dec 14, 2020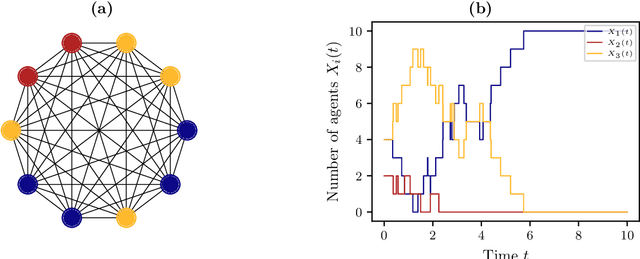

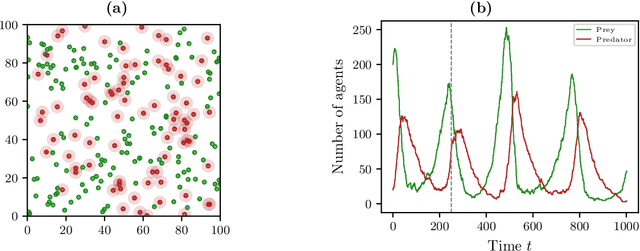

Abstract:The dynamical behavior of social systems can be described by agent-based models. Although single agents follow easily explainable rules, complex time-evolving patterns emerge due to their interaction. The simulation and analysis of such agent-based models, however, is often prohibitively time-consuming if the number of agents is large. In this paper, we show how Koopman operator theory can be used to derive reduced models of agent-based systems using only simulation or real-world data. Our goal is to learn coarse-grained models and to represent the reduced dynamics by ordinary or stochastic differential equations. The new variables are, for instance, aggregated state variables of the agent-based model, modeling the collective behavior of larger groups or the entire population. Using benchmark problems with known coarse-grained models, we demonstrate that the obtained reduced systems are in good agreement with the analytical results, provided that the numbers of agents is sufficiently large.
Feature space approximation for kernel-based supervised learning
Nov 25, 2020
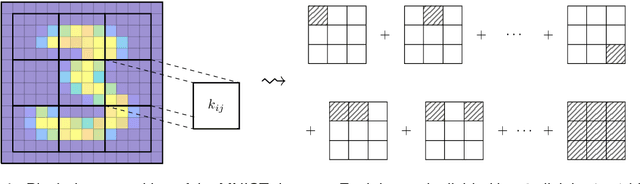
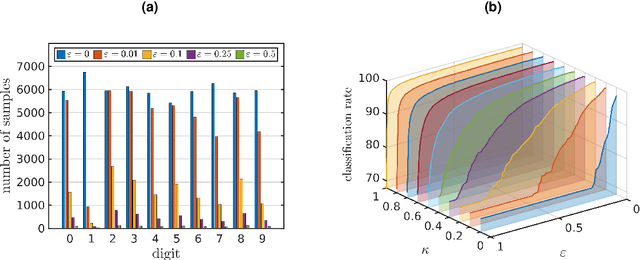
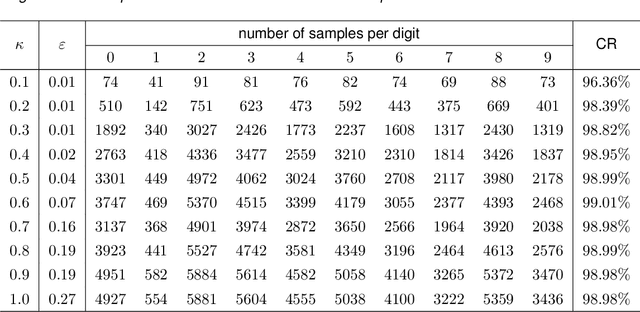
Abstract:We propose a method for the approximation of high- or even infinite-dimensional feature vectors, which play an important role in supervised learning. The goal is to reduce the size of the training data, resulting in lower storage consumption and computational complexity. Furthermore, the method can be regarded as a regularization technique, which improves the generalizability of learned target functions. We demonstrate significant improvements in comparison to the computation of data-driven predictions involving the full training data set. The method is applied to classification and regression problems from different application areas such as image recognition, system identification, and oceanographic time series analysis.
Kernel autocovariance operators of stationary processes: Estimation and convergence
Apr 02, 2020Abstract:We consider autocovariance operators of a stationary stochastic process on a Polish space that is embedded into a reproducing kernel Hilbert space. We investigate how empirical estimates of these operators converge along realizations of the process under various conditions. In particular, we examine ergodic and strongly mixing processes and prove several asymptotic results as well as finite sample error bounds with a detailed analysis for the Gaussian kernel. We provide applications of our theory in terms of consistency results for kernel PCA with dependent data and the conditional mean embedding of transition probabilities. Finally, we use our approach to examine the nonparametric estimation of Markov transition operators and highlight how our theory can give a consistency analysis for a large family of spectral analysis methods including kernel-based dynamic mode decomposition.
Data-driven approximation of the Koopman generator: Model reduction, system identification, and control
Sep 23, 2019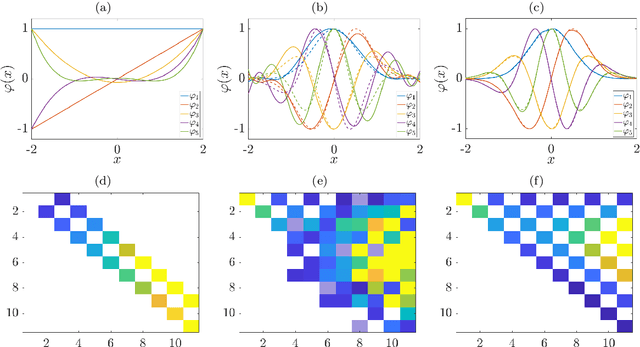
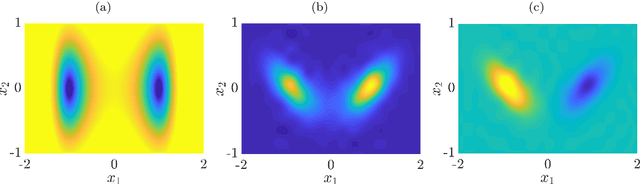
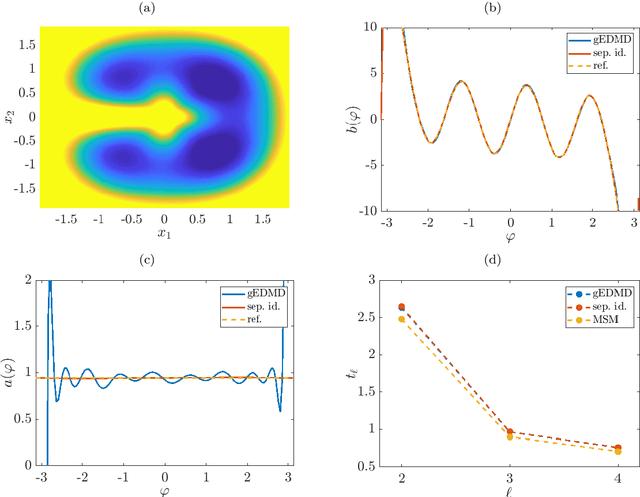
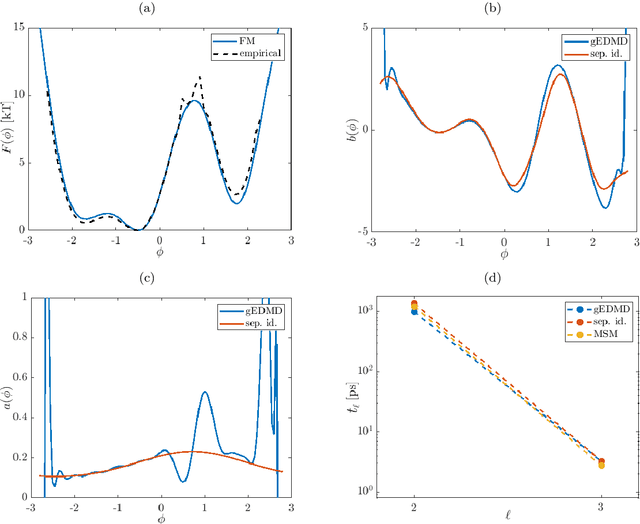
Abstract:We derive a data-driven method for the approximation of the Koopman generator called gEDMD, which can be regarded as a straightforward extension of EDMD (extended dynamic mode decomposition). This approach is applicable to deterministic and stochastic dynamical systems. It can be used for computing eigenvalues, eigenfunctions, and modes of the generator and for system identification. In addition to learning the governing equations of deterministic systems, which then reduces to SINDy (sparse identification of nonlinear dynamics), it is possible to identify the drift and diffusion terms of stochastic differential equations from data. Moreover, we apply gEDMD to derive coarse-grained models of high-dimensional systems, and also to determine efficient model predictive control strategies. We highlight relationships with other methods and demonstrate the efficacy of the proposed methods using several guiding examples and prototypical molecular dynamics problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge