Symmetric and antisymmetric kernels for machine learning problems in quantum physics and chemistry

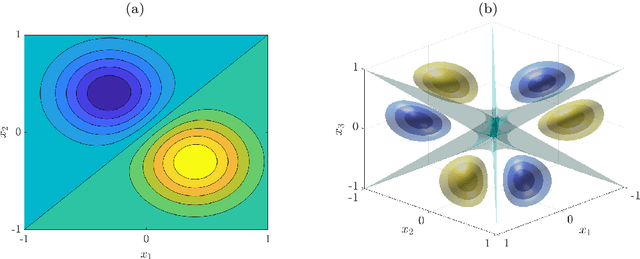
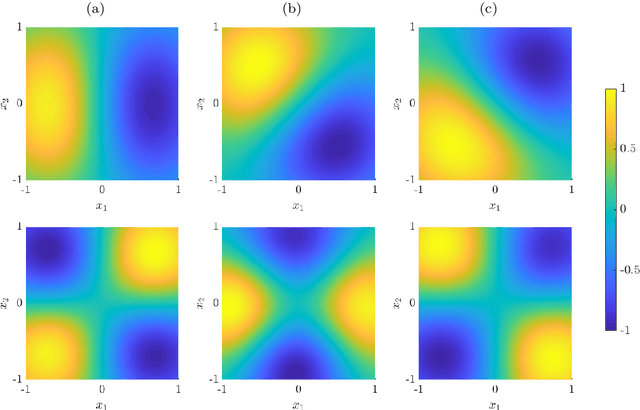
We derive symmetric and antisymmetric kernels by symmetrizing and antisymmetrizing conventional kernels and analyze their properties. In particular, we compute the feature space dimensions of the resulting polynomial kernels, prove that the reproducing kernel Hilbert spaces induced by symmetric and antisymmetric Gaussian kernels are dense in the space of symmetric and antisymmetric functions, and propose a Slater determinant representation of the antisymmetric Gaussian kernel, which allows for an efficient evaluation even if the state space is high-dimensional. Furthermore, we show that by exploiting symmetries or antisymmetries the size of the training data set can be significantly reduced. The results are illustrated with guiding examples and simple quantum physics and chemistry applications.

Feature space approximation for kernel-based supervised learning

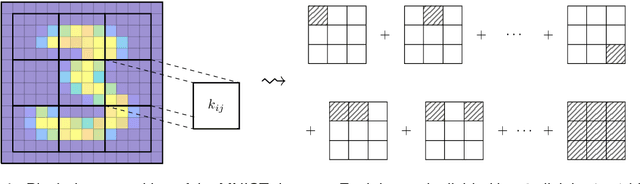
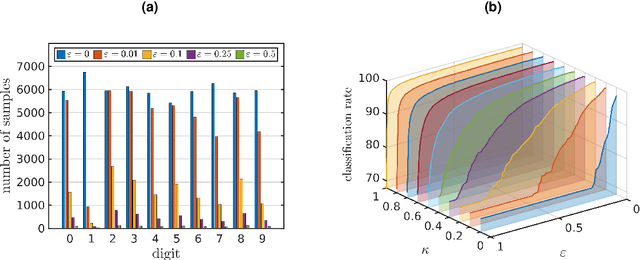
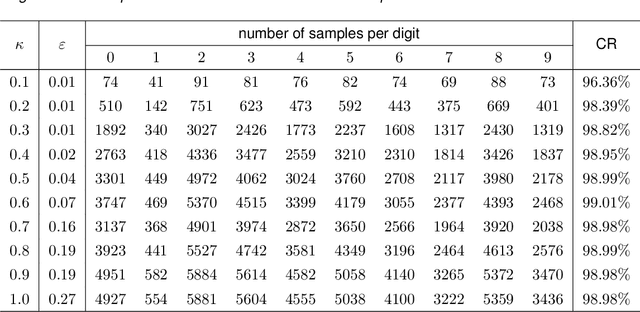
We propose a method for the approximation of high- or even infinite-dimensional feature vectors, which play an important role in supervised learning. The goal is to reduce the size of the training data, resulting in lower storage consumption and computational complexity. Furthermore, the method can be regarded as a regularization technique, which improves the generalizability of learned target functions. We demonstrate significant improvements in comparison to the computation of data-driven predictions involving the full training data set. The method is applied to classification and regression problems from different application areas such as image recognition, system identification, and oceanographic time series analysis.

Tensor-based algorithms for image classification

The interest in machine learning with tensor networks has been growing rapidly in recent years. The goal is to exploit tensor-structured basis functions in order to generate exponentially large feature spaces which are then used for supervised learning. We will propose two different tensor approaches for quantum-inspired machine learning. One is a kernel-based reformulation of the previously introduced MANDy, the other an alternating ridge regression in the tensor-train format. We will apply both methods to the MNIST and fashion MNIST data set and compare the results with state-of-the-art neural network-based classifiers.

Tensor-based EDMD for the Koopman analysis of high-dimensional systems

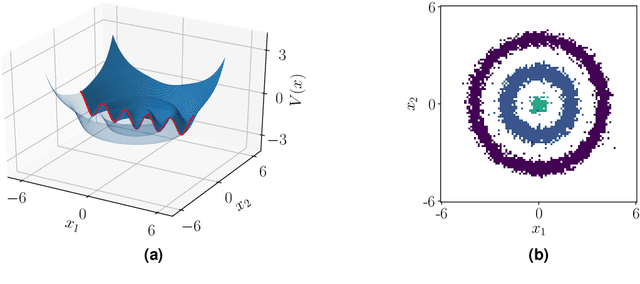
Recent years have seen rapid advances in the data-driven analysis of dynamical systems based on Koopman operator theory -- with extended dynamic mode decomposition (EDMD) being a cornerstone of the field. On the other hand, low-rank tensor product approximations -- in particular the tensor train (TT) format -- have become a valuable tool for the solution of large-scale problems in a number of fields. In this work, we combine EDMD and the TT format, enabling the application of EDMD to high-dimensional problems in conjunction with a large set of features. We present the construction of different TT representations of tensor-structured data arrays. Furthermore, we also derive efficient algorithms to solve the EDMD eigenvalue problem based on those representations and to project the data into a low-dimensional representation defined by the eigenvectors. We prove that there is a physical interpretation of the procedure and demonstrate its capabilities by applying the method to benchmark data sets of molecular dynamics simulation.