Partial observations, coarse graining and equivariance in Koopman operator theory for large-scale dynamical systems

The Koopman operator has become an essential tool for data-driven analysis, prediction and control of complex systems, the main reason being the enormous potential of identifying linear function space representations of nonlinear dynamics from measurements. Until now, the situation where for large-scale systems, we (i) only have access to partial observations (i.e., measurements, as is very common for experimental data) or (ii) deliberately perform coarse graining (for efficiency reasons) has not been treated to its full extent. In this paper, we address the pitfall associated with this situation, that the classical EDMD algorithm does not automatically provide a Koopman operator approximation for the underlying system if we do not carefully select the number of observables. Moreover, we show that symmetries in the system dynamics can be carried over to the Koopman operator, which allows us to massively increase the model efficiency. We also briefly draw a connection to domain decomposition techniques for partial differential equations and present numerical evidence using the Kuramoto--Sivashinsky equation.

Symmetric and antisymmetric kernels for machine learning problems in quantum physics and chemistry

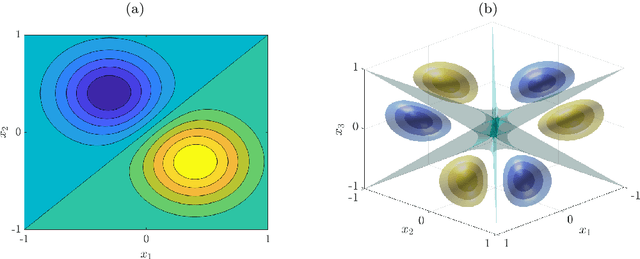
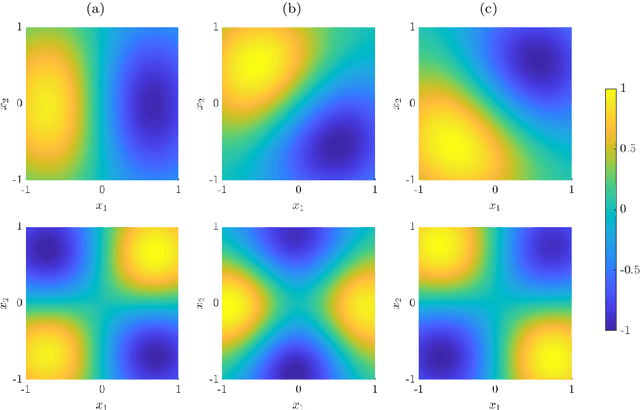
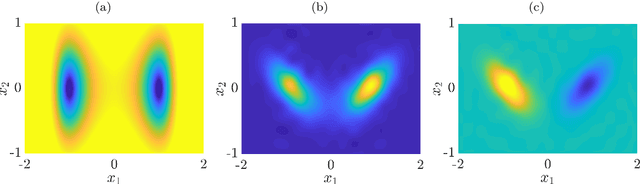
We derive symmetric and antisymmetric kernels by symmetrizing and antisymmetrizing conventional kernels and analyze their properties. In particular, we compute the feature space dimensions of the resulting polynomial kernels, prove that the reproducing kernel Hilbert spaces induced by symmetric and antisymmetric Gaussian kernels are dense in the space of symmetric and antisymmetric functions, and propose a Slater determinant representation of the antisymmetric Gaussian kernel, which allows for an efficient evaluation even if the state space is high-dimensional. Furthermore, we show that by exploiting symmetries or antisymmetries the size of the training data set can be significantly reduced. The results are illustrated with guiding examples and simple quantum physics and chemistry applications.

Kernel-based approximation of the Koopman generator and Schrödinger operator

Many dimensionality and model reduction techniques rely on estimating dominant eigenfunctions of associated dynamical operators from data. Important examples include the Koopman operator and its generator, but also the Schr\"odinger operator. We propose a kernel-based method for the approximation of differential operators in reproducing kernel Hilbert spaces and show how eigenfunctions can be estimated by solving auxiliary matrix eigenvalue problems. The resulting algorithms are applied to molecular dynamics and quantum chemistry examples. Furthermore, we exploit that, under certain conditions, the Schr\"odinger operator can be transformed into a Kolmogorov backward operator corresponding to a drift-diffusion process and vice versa. This allows us to apply methods developed for the analysis of high-dimensional stochastic differential equations to quantum mechanical systems.

Data-driven approximation of the Koopman generator: Model reduction, system identification, and control

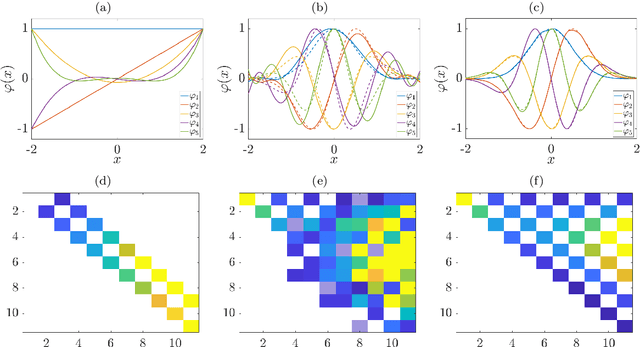
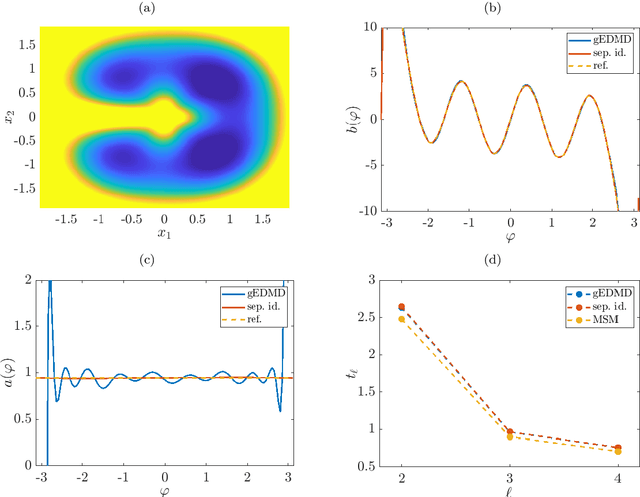
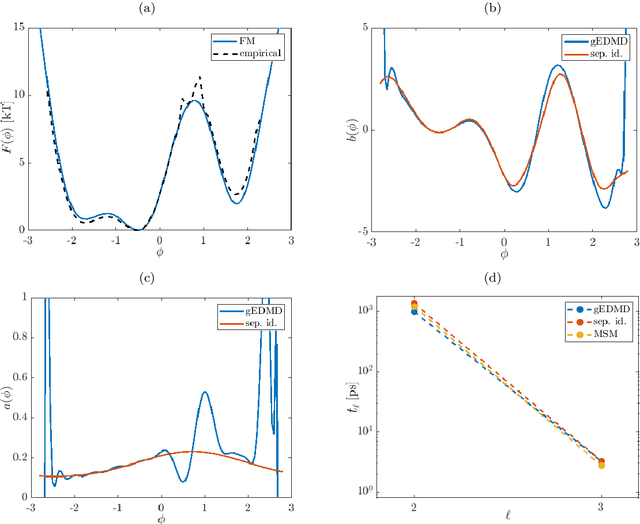
We derive a data-driven method for the approximation of the Koopman generator called gEDMD, which can be regarded as a straightforward extension of EDMD (extended dynamic mode decomposition). This approach is applicable to deterministic and stochastic dynamical systems. It can be used for computing eigenvalues, eigenfunctions, and modes of the generator and for system identification. In addition to learning the governing equations of deterministic systems, which then reduces to SINDy (sparse identification of nonlinear dynamics), it is possible to identify the drift and diffusion terms of stochastic differential equations from data. Moreover, we apply gEDMD to derive coarse-grained models of high-dimensional systems, and also to determine efficient model predictive control strategies. We highlight relationships with other methods and demonstrate the efficacy of the proposed methods using several guiding examples and prototypical molecular dynamics problems.

Tensor-based EDMD for the Koopman analysis of high-dimensional systems

Recent years have seen rapid advances in the data-driven analysis of dynamical systems based on Koopman operator theory -- with extended dynamic mode decomposition (EDMD) being a cornerstone of the field. On the other hand, low-rank tensor product approximations -- in particular the tensor train (TT) format -- have become a valuable tool for the solution of large-scale problems in a number of fields. In this work, we combine EDMD and the TT format, enabling the application of EDMD to high-dimensional problems in conjunction with a large set of features. We present the construction of different TT representations of tensor-structured data arrays. Furthermore, we also derive efficient algorithms to solve the EDMD eigenvalue problem based on those representations and to project the data into a low-dimensional representation defined by the eigenvectors. We prove that there is a physical interpretation of the procedure and demonstrate its capabilities by applying the method to benchmark data sets of molecular dynamics simulation.

Sparse learning of stochastic dynamic equations

With the rapid increase of available data for complex systems, there is great interest in the extraction of physically relevant information from massive datasets. Recently, a framework called Sparse Identification of Nonlinear Dynamics (SINDy) has been introduced to identify the governing equations of dynamical systems from simulation data. In this study, we extend SINDy to stochastic dynamical systems, which are frequently used to model biophysical processes. We prove the asymptotic correctness of stochastics SINDy in the infinite data limit, both in the original and projected variables. We discuss algorithms to solve the sparse regression problem arising from the practical implementation of SINDy, and show that cross validation is an essential tool to determine the right level of sparsity. We demonstrate the proposed methodology on two test systems, namely, the diffusion in a one-dimensional potential, and the projected dynamics of a two-dimensional diffusion process.

Variational Koopman models: slow collective variables and molecular kinetics from short off-equilibrium simulations

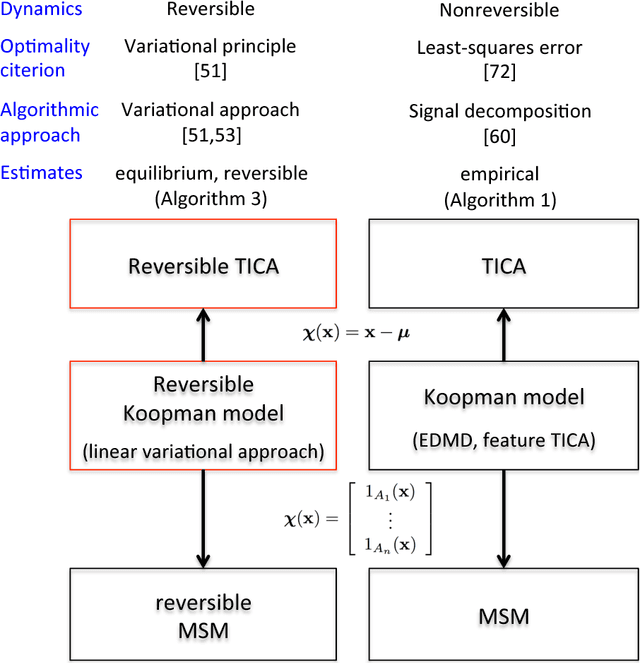
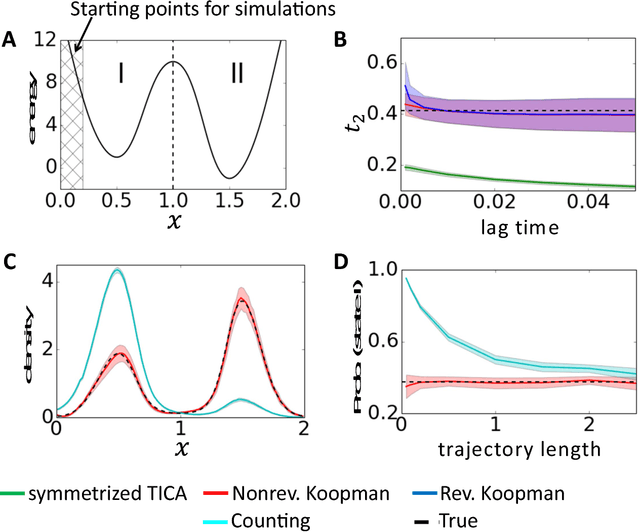
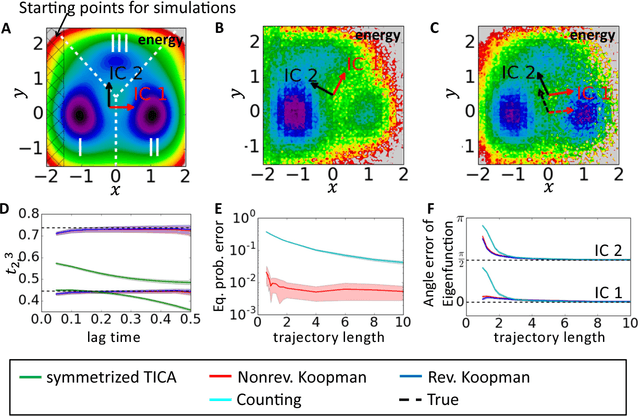
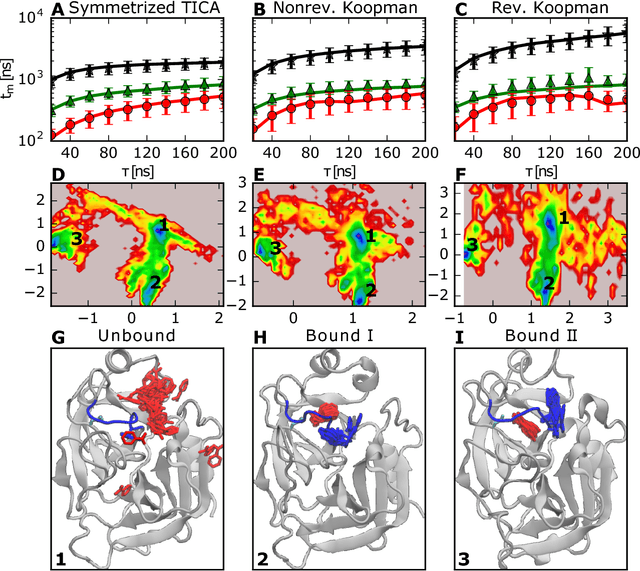
Markov state models (MSMs) and Master equation models are popular approaches to approximate molecular kinetics, equilibria, metastable states, and reaction coordinates in terms of a state space discretization usually obtained by clustering. Recently, a powerful generalization of MSMs has been introduced, the variational approach (VA) of molecular kinetics and its special case the time-lagged independent component analysis (TICA), which allow us to approximate slow collective variables and molecular kinetics by linear combinations of smooth basis functions or order parameters. While it is known how to estimate MSMs from trajectories whose starting points are not sampled from an equilibrium ensemble, this has not yet been the case for TICA and the VA. Previous estimates from short trajectories, have been strongly biased and thus not variationally optimal. Here, we employ Koopman operator theory and ideas from dynamic mode decomposition (DMD) to extend the VA and TICA to non-equilibrium data. The main insight is that the VA and TICA provide a coefficient matrix that we call Koopman model, as it approximates the underlying dynamical (Koopman) operator in conjunction with the basis set used. This Koopman model can be used to compute a stationary vector to reweight the data to equilibrium. From such a Koopman-reweighted sample, equilibrium expectation values and variationally optimal reversible Koopman models can be constructed even with short simulations. The Koopman model can be used to propagate densities, and its eigenvalue decomposition provide estimates of relaxation timescales and slow collective variables for dimension reduction. Koopman models are generalizations of Markov state models, TICA and the linear VA and allow molecular kinetics to be described without a cluster discretization.