SafEDMD: A certified learning architecture tailored to data-driven control of nonlinear dynamical systems

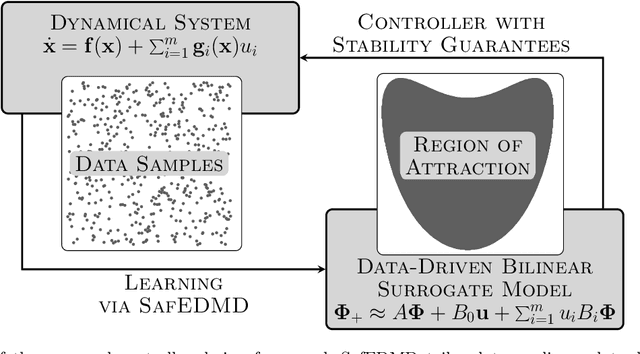
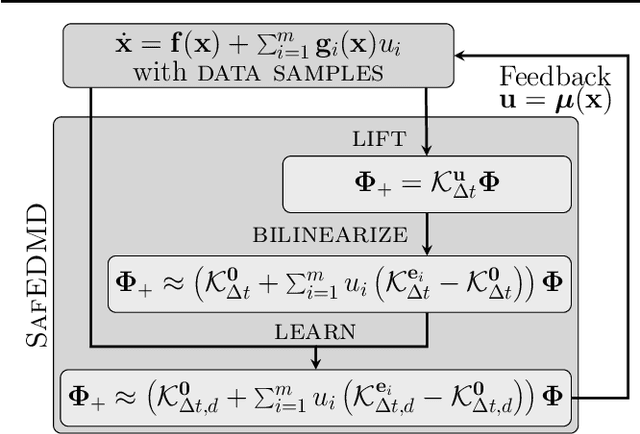
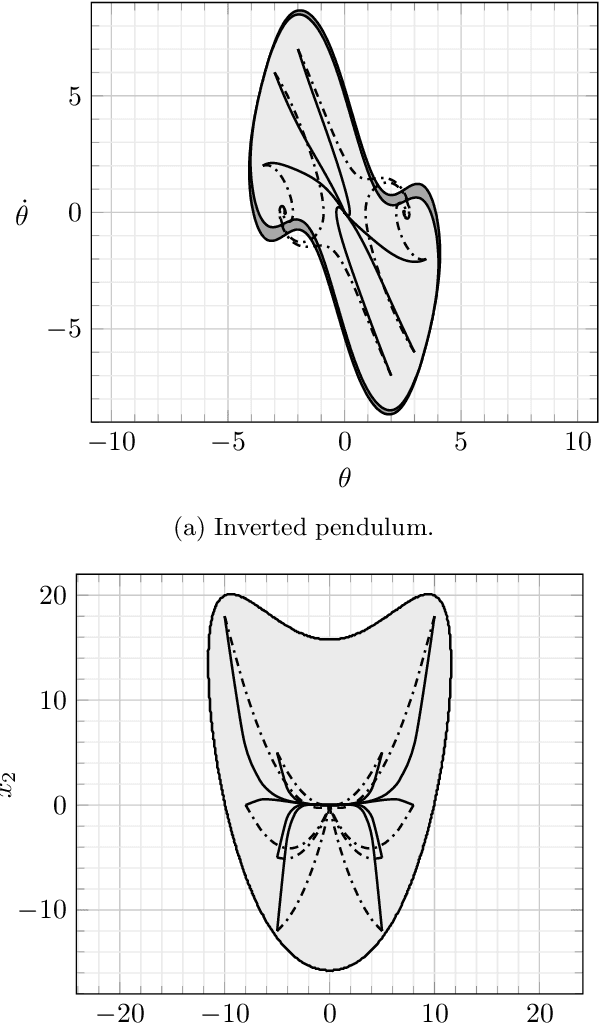
The Koopman operator serves as the theoretical backbone for machine learning of dynamical control systems, where the operator is heuristically approximated by extended dynamic mode decomposition (EDMD). In this paper, we propose Stability- and certificate-oriented EDMD (SafEDMD): a novel EDMD-based learning architecture which comes along with rigorous certificates, resulting in a reliable surrogate model generated in a data-driven fashion. To ensure trustworthiness of SafEDMD, we derive proportional error bounds, which vanish at the origin and are tailored for control tasks, leading to certified controller design based on semi-definite programming. We illustrate the developed machinery by means of several benchmark examples and highlight the advantages over state-of-the-art methods.

Partial observations, coarse graining and equivariance in Koopman operator theory for large-scale dynamical systems

The Koopman operator has become an essential tool for data-driven analysis, prediction and control of complex systems, the main reason being the enormous potential of identifying linear function space representations of nonlinear dynamics from measurements. Until now, the situation where for large-scale systems, we (i) only have access to partial observations (i.e., measurements, as is very common for experimental data) or (ii) deliberately perform coarse graining (for efficiency reasons) has not been treated to its full extent. In this paper, we address the pitfall associated with this situation, that the classical EDMD algorithm does not automatically provide a Koopman operator approximation for the underlying system if we do not carefully select the number of observables. Moreover, we show that symmetries in the system dynamics can be carried over to the Koopman operator, which allows us to massively increase the model efficiency. We also briefly draw a connection to domain decomposition techniques for partial differential equations and present numerical evidence using the Kuramoto--Sivashinsky equation.