Verifiable Regularity Criterion for Conditional Expectation Operators and Conditional Mean Embeddings with Applications to Nonparametric Regression, Bayesian Inverse Problems, and Koopman Operators

Conditional expectation operators (CEOs) and their associated conditional mean embeddings (CMEs) play a central role across applied mathematics and machine learning, appearing in nonparametric regression, Bayesian inverse problems, and Koopman operator theory. A fundamental question is when a CEO maps a function space on $\mathcal{Y}$ into a prescribed function space on $\mathcal{X}$, particularly a reproducing kernel Hilbert space (RKHS). We show that such mapping properties are characterized by the regularity of the Radon--Nikodym density of the conditional law, and establish a simple, verifiable sufficient condition under which the CEO is bounded and Hilbert--Schmidt. For RKHSs norm-equivalent to Sobolev spaces, this condition reduces to Sobolev regularity of the conditional density. The result yields a direct route to validate CME representations and error bounds for Galerkin-type and CME-based estimators. We verify the regularity condition in three settings: nonparametric regression, Bayesian inverse problems, and Koopman operator theory for stochastic dynamical systems. We show in each case that classical regularity results on the underlying probabilistic model imply the required mapping properties. The resulting framework offers a unified perspective on conditional expectation operators across probability, operator theory, kernel methods, and stochastic dynamics.

Koopman operator theory: fundamentals, control, and applications

The Koopman operator has gained considerable attention due to its ability to provide a global linear representation of highly complex dynamical systems. The operator describes nonlinear dynamics in a linear way through the lens of real- or complex-valued observable functions. Recently proposed data-driven techniques, like extended dynamic mode decomposition (EDMD), its kernelized variant, and machine-learning methods, can be used to generate finite-dimensional approximations accompanied by finite-data error bounds. In this tutorial paper, we provide a concise introduction into Koopman operator theory and its use in systems and control. A particular focus is put on data-driven surrogate models, their extension to systems with inputs, and controller design using Koopman operator theory. Moreover, we demonstrate the key techniques, i.e., EDMD and Koopman MPC. To this end, we provide simulation studies including source code on GitHub to enable the interested reader to experience the Koopman operator in systems and control step by step.

Data-Driven Predictive Control of Nonholonomic Robots Based on a Bilinear Koopman Realization: Data Does Not Replace Geometry

Advances in machine learning and the growing trend towards effortless data generation in real-world systems has led to an increasing interest for data-inferred models and data-based control in robotics. It seems appealing to govern robots solely based on data, bypassing the traditional, more elaborate pipeline of system modeling through first-principles and subsequent controller design. One promising data-driven approach is the Extended Dynamic Mode Decomposition (EDMD) for control-affine systems, a system class which contains many vehicles and machines of immense practical importance including, e.g., typical wheeled mobile robots. EDMD can be highly data-efficient, computationally inexpensive, can deal with nonlinear dynamics as prevalent in robotics and mechanics, and has a sound theoretical foundation rooted in Koopman theory. On this background, this present paper examines how EDMD models can be integrated into predictive controllers for nonholonomic mobile robots. In addition to the conventional kinematic mobile robot, we also cover the complete data-driven control pipeline - from data acquisition to control design - when the robot is not treated in terms of first-order kinematics but in a second-order manner, allowing to account for actuator dynamics. Using only real-world measurement data, it is shown in both simulations and hardware experiments that the surrogate models enable high-precision predictive controllers in the studied cases. However, the findings raise significant concerns about purely data-centric approaches that overlook the underlying geometry of nonholonomic systems, showing that, for nonholonomic systems, some geometric insight seems necessary and cannot be easily compensated for with large amounts of data.

SafEDMD: A certified learning architecture tailored to data-driven control of nonlinear dynamical systems

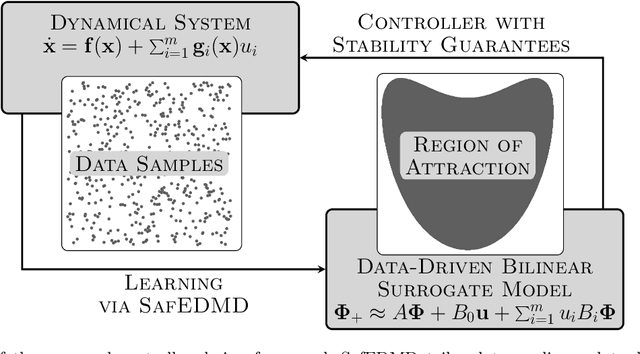
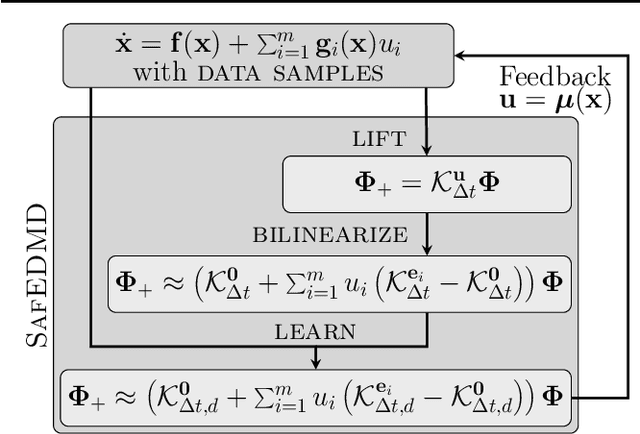
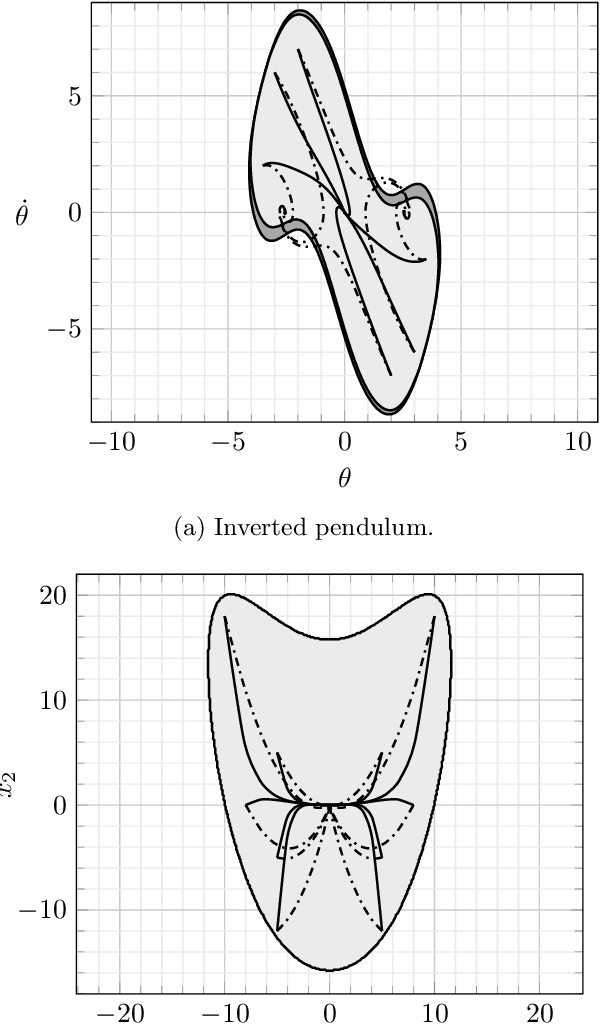
The Koopman operator serves as the theoretical backbone for machine learning of dynamical control systems, where the operator is heuristically approximated by extended dynamic mode decomposition (EDMD). In this paper, we propose Stability- and certificate-oriented EDMD (SafEDMD): a novel EDMD-based learning architecture which comes along with rigorous certificates, resulting in a reliable surrogate model generated in a data-driven fashion. To ensure trustworthiness of SafEDMD, we derive proportional error bounds, which vanish at the origin and are tailored for control tasks, leading to certified controller design based on semi-definite programming. We illustrate the developed machinery by means of several benchmark examples and highlight the advantages over state-of-the-art methods.

Partial observations, coarse graining and equivariance in Koopman operator theory for large-scale dynamical systems

The Koopman operator has become an essential tool for data-driven analysis, prediction and control of complex systems, the main reason being the enormous potential of identifying linear function space representations of nonlinear dynamics from measurements. Until now, the situation where for large-scale systems, we (i) only have access to partial observations (i.e., measurements, as is very common for experimental data) or (ii) deliberately perform coarse graining (for efficiency reasons) has not been treated to its full extent. In this paper, we address the pitfall associated with this situation, that the classical EDMD algorithm does not automatically provide a Koopman operator approximation for the underlying system if we do not carefully select the number of observables. Moreover, we show that symmetries in the system dynamics can be carried over to the Koopman operator, which allows us to massively increase the model efficiency. We also briefly draw a connection to domain decomposition techniques for partial differential equations and present numerical evidence using the Kuramoto--Sivashinsky equation.

On Koopman-based surrogate models for non-holonomic robots

Data-driven surrogate models of dynamical systems based on the extended dynamic mode decomposition are nowadays well-established and widespread in applications. Further, for non-holonomic systems exhibiting a multiplicative coupling between states and controls, the usage of bi-linear surrogate models has proven beneficial. However, an in-depth analysis of the approximation quality and its dependence on different hyperparameters based on both simulation and experimental data is still missing. We investigate a differential-drive mobile robot to close this gap and provide first guidelines on the systematic design of data-efficient surrogate models.

Path Planning for Concentric Tube Robots: a Toolchain with Application to Stereotactic Neurosurgery

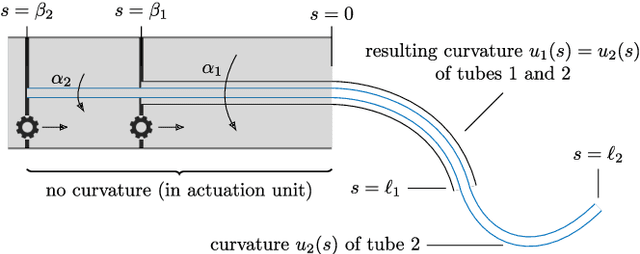
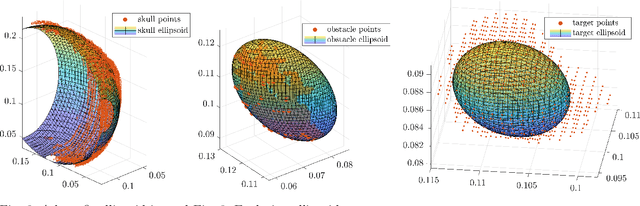
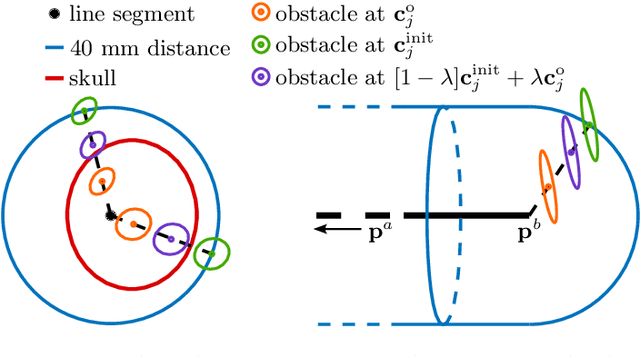
We present a toolchain for solving path planning problems for concentric tube robots through obstacle fields. First, ellipsoidal sets representing the target area and obstacles are constructed from labelled point clouds. Then, the nonlinear and highly nonconvex optimal control problem is solved by introducing a homotopy on the obstacle positions where at one extreme of the parameter the obstacles are removed from the operating space, and at the other extreme they are located at their intended positions. We present a detailed example (with more than a thousand obstacles) from stereotactic neurosurgery with real-world data obtained from labelled MPRI scans.