Efficient Avoidance of Ellipsoidal Obstacles with Model Predictive Control for Mobile Robots and Vehicles

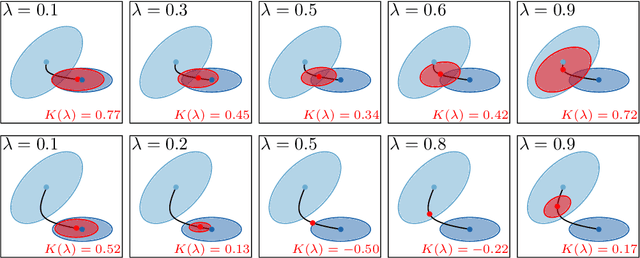
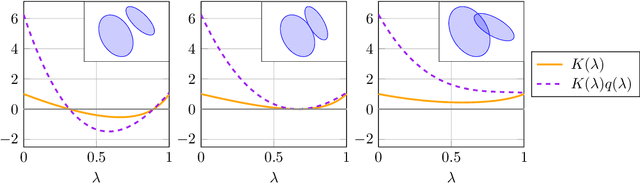
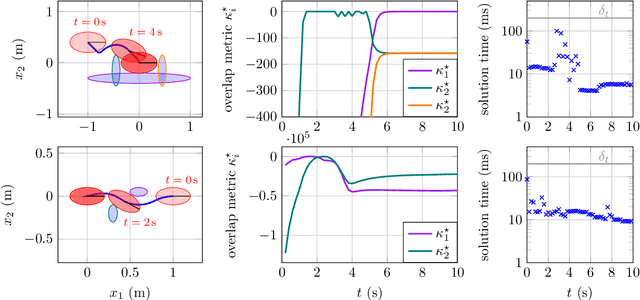
In real-world applications of mobile robots, collision avoidance is of critical importance. Typically, global motion planning in constrained environments is addressed through high-level control schemes. However, additionally integrating local collision avoidance into robot motion control offers significant advantages. For instance, it reduces the reliance on heuristics and conservatism that can arise from a two-stage approach separating local collision avoidance and control. Moreover, using model predictive control (MPC), a robot's full potential can be harnessed by considering jointly local collision avoidance, the robot's dynamics, and actuation constraints. In this context, the present paper focuses on obstacle avoidance for wheeled mobile robots, where both the robot's and obstacles' occupied volumes are modeled as ellipsoids. To this end, a computationally efficient overlap test, that works for arbitrary ellipsoids, is conducted and novelly integrated into the MPC framework. We propose a particularly efficient implementation tailored to robots moving in the plane. The functionality of the proposed obstacle-avoiding MPC is demonstrated for two exemplary types of kinematics by means of simulations. A hardware experiment using a real-world wheeled mobile robot shows transferability to reality and real-time applicability. The general computational approach to ellipsoidal obstacle avoidance can also be applied to other robotic systems and vehicles as well as three-dimensional scenarios.

The impact of AI on engineering design procedures for dynamical systems

Artificial intelligence (AI) is driving transformative changes across numerous fields, revolutionizing conventional processes and creating new opportunities for innovation. The development of mechatronic systems is undergoing a similar transformation. Over the past decade, modeling, simulation, and optimization techniques have become integral to the design process, paving the way for the adoption of AI-based methods. In this paper, we examine the potential for integrating AI into the engineering design process, using the V-model from the VDI guideline 2206, considered the state-of-the-art in product design, as a foundation. We identify and classify AI methods based on their suitability for specific stages within the engineering product design workflow. Furthermore, we present a series of application examples where AI-assisted design has been successfully implemented by the authors. These examples, drawn from research projects within the DFG Priority Program \emph{SPP~2353: Daring More Intelligence - Design Assistants in Mechanics and Dynamics}, showcase a diverse range of applications across mechanics and mechatronics, including areas such as acoustics and robotics.

The Indirect Method for Generating Libraries of Optimal Periodic Trajectories and Its Application to Economical Bipedal Walking

Trajectory optimization is an essential tool for generating efficient and dynamically consistent gaits in legged locomotion. This paper explores the indirect method of trajectory optimization, emphasizing its application in creating optimal periodic gaits for legged systems and contrasting it with the more commonly used direct method. While the direct method provides considerable flexibility in its implementation, it is limited by its input space parameterization. In contrast, the indirect method improves accuracy by defining control inputs as functions of the system's states and costates. We tackle the convergence challenges associated with indirect shooting methods, particularly through the systematic development of gait libraries by utilizing numerical continuation methods. Our contributions include: (1) the formalization of a general periodic trajectory optimization problem that extends existing first-order necessary conditions for a broader range of cost functions and operating conditions; (2) a methodology for efficiently generating libraries of optimal trajectories (gaits) utilizing a single shooting approach combined with numerical continuation methods, including a novel approach for reconstructing Lagrange multipliers and costates from passive gaits; and (3) a comparative analysis of the indirect and direct shooting methods using a compass-gait walker as a case study, demonstrating the former's superior accuracy in generating optimal gaits. The findings underscore the potential of the indirect method for generating families of optimal gaits, thereby advancing the field of trajectory optimization in legged robotics.

An iterative closest point algorithm for marker-free 3D shape registration of continuum robots

Continuum robots have emerged as a promising technology in the medical field due to their potential of accessing deep sited locations of the human body with low surgical trauma. When deriving physics-based models for these robots, evaluating the models poses a significant challenge due to the difficulty in accurately measuring their intricate shapes. In this work, we present an optimization based 3D shape registration algorithm for estimation of the backbone shape of slender continuum robots as part of a pho togrammetric measurement. Our approach to estimating the backbones optimally matches a parametric three-dimensional curve to images of the robot. Since we incorporate an iterative closest point algorithm into our method, we do not need prior knowledge of the robots position within the respective images. In our experiments with artificial and real images of a concentric tube continuum robot, we found an average maximum deviation of the reconstruction from simulation data of 0.665 mm and 0.939 mm from manual measurements. These results show that our algorithm is well capable of producing high accuracy positional data from images of continuum robots.

Optimization-based motion primitive automata for autonomous driving

Trajectory planning for autonomous cars can be addressed by primitive-based methods, which encode nonlinear dynamical system behavior into automata. In this paper, we focus on optimal trajectory planning. Since, typically, multiple criteria have to be taken into account, multiobjective optimization problems have to be solved. For the resulting Pareto-optimal motion primitives, we introduce a universal automaton, which can be reduced or reconfigured according to prioritized criteria during planning. We evaluate a corresponding multi-vehicle planning scenario with both simulations and laboratory experiments.

Hamiltonian Neural Networks with Automatic Symmetry Detection

Recently, Hamiltonian neural networks (HNN) have been introduced to incorporate prior physical knowledge when learning the dynamical equations of Hamiltonian systems. Hereby, the symplectic system structure is preserved despite the data-driven modeling approach. However, preserving symmetries requires additional attention. In this research, we enhance the HNN with a Lie algebra framework to detect and embed symmetries in the neural network. This approach allows to simultaneously learn the symmetry group action and the total energy of the system. As illustrating examples, a pendulum on a cart and a two-body problem from astrodynamics are considered.

Path Planning for Concentric Tube Robots: a Toolchain with Application to Stereotactic Neurosurgery

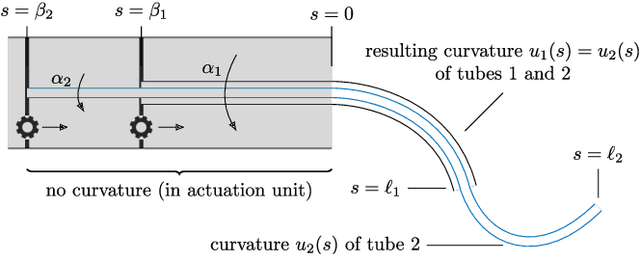
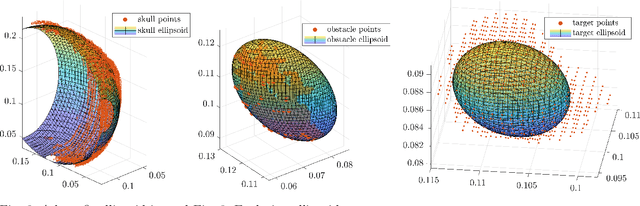
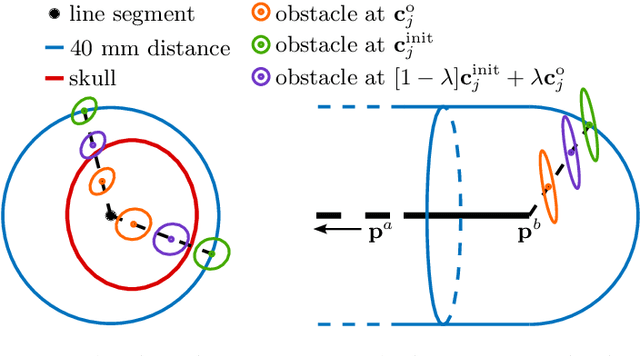
We present a toolchain for solving path planning problems for concentric tube robots through obstacle fields. First, ellipsoidal sets representing the target area and obstacles are constructed from labelled point clouds. Then, the nonlinear and highly nonconvex optimal control problem is solved by introducing a homotopy on the obstacle positions where at one extreme of the parameter the obstacles are removed from the operating space, and at the other extreme they are located at their intended positions. We present a detailed example (with more than a thousand obstacles) from stereotactic neurosurgery with real-world data obtained from labelled MPRI scans.

Optimization Strategies for Real-Time Control of an Autonomous Melting Probe

We present an optimization-based approach for trajectory planning and control of a maneuverable melting probe with a high number of binary control variables. The dynamics of the system are modeled by a set of ordinary differential equations with a priori knowledge of system parameters of the melting process. The original planning problem is handled as an optimal control problem. Then, optimal control is used for reference trajectory planning as well as in an MPC-like algorithm. Finally, to determine binary control variables, a MINLP fitting approach is presented. The proposed strategy has recently been tested during experiments on the Langenferner glacier. The data obtained is used for model improvement by means of automated parameter identification.