Hamiltonian Neural Networks with Automatic Symmetry Detection

Recently, Hamiltonian neural networks (HNN) have been introduced to incorporate prior physical knowledge when learning the dynamical equations of Hamiltonian systems. Hereby, the symplectic system structure is preserved despite the data-driven modeling approach. However, preserving symmetries requires additional attention. In this research, we enhance the HNN with a Lie algebra framework to detect and embed symmetries in the neural network. This approach allows to simultaneously learn the symmetry group action and the total energy of the system. As illustrating examples, a pendulum on a cart and a two-body problem from astrodynamics are considered.

Discrete Lagrangian Neural Networks with Automatic Symmetry Discovery

By one of the most fundamental principles in physics, a dynamical system will exhibit those motions which extremise an action functional. This leads to the formation of the Euler-Lagrange equations, which serve as a model of how the system will behave in time. If the dynamics exhibit additional symmetries, then the motion fulfils additional conservation laws, such as conservation of energy (time invariance), momentum (translation invariance), or angular momentum (rotational invariance). To learn a system representation, one could learn the discrete Euler-Lagrange equations, or alternatively, learn the discrete Lagrangian function $\mathcal{L}_d$ which defines them. Based on ideas from Lie group theory, in this work we introduce a framework to learn a discrete Lagrangian along with its symmetry group from discrete observations of motions and, therefore, identify conserved quantities. The learning process does not restrict the form of the Lagrangian, does not require velocity or momentum observations or predictions and incorporates a cost term which safeguards against unwanted solutions and against potential numerical issues in forward simulations. The learnt discrete quantities are related to their continuous analogues using variational backward error analysis and numerical results demonstrate the improvement such models can have both qualitatively and quantitatively even in the presence of noise.

Efficient time stepping for numerical integration using reinforcement learning

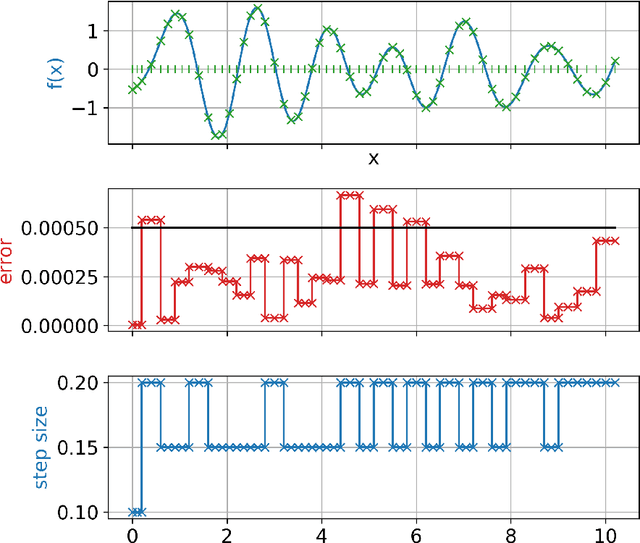
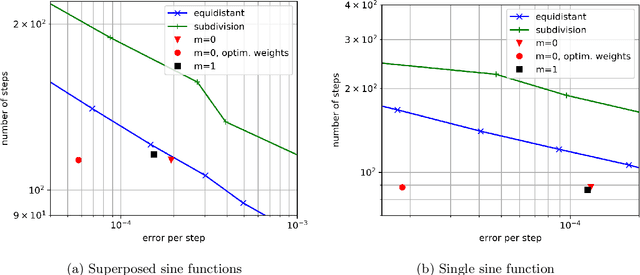
Many problems in science and engineering require the efficient numerical approximation of integrals, a particularly important application being the numerical solution of initial value problems for differential equations. For complex systems, an equidistant discretization is often inadvisable, as it either results in prohibitively large errors or computational effort. To this end, adaptive schemes have been developed that rely on error estimators based on Taylor series expansions. While these estimators a) rely on strong smoothness assumptions and b) may still result in erroneous steps for complex systems (and thus require step rejection mechanisms), we here propose a data-driven time stepping scheme based on machine learning, and more specifically on reinforcement learning (RL) and meta-learning. First, one or several (in the case of non-smooth or hybrid systems) base learners are trained using RL. Then, a meta-learner is trained which (depending on the system state) selects the base learner that appears to be optimal for the current situation. Several examples including both smooth and non-smooth problems demonstrate the superior performance of our approach over state-of-the-art numerical schemes. The code is available under https://github.com/lueckem/quadrature-ML.