Discrete Lagrangian Neural Networks with Automatic Symmetry Discovery

By one of the most fundamental principles in physics, a dynamical system will exhibit those motions which extremise an action functional. This leads to the formation of the Euler-Lagrange equations, which serve as a model of how the system will behave in time. If the dynamics exhibit additional symmetries, then the motion fulfils additional conservation laws, such as conservation of energy (time invariance), momentum (translation invariance), or angular momentum (rotational invariance). To learn a system representation, one could learn the discrete Euler-Lagrange equations, or alternatively, learn the discrete Lagrangian function $\mathcal{L}_d$ which defines them. Based on ideas from Lie group theory, in this work we introduce a framework to learn a discrete Lagrangian along with its symmetry group from discrete observations of motions and, therefore, identify conserved quantities. The learning process does not restrict the form of the Lagrangian, does not require velocity or momentum observations or predictions and incorporates a cost term which safeguards against unwanted solutions and against potential numerical issues in forward simulations. The learnt discrete quantities are related to their continuous analogues using variational backward error analysis and numerical results demonstrate the improvement such models can have both qualitatively and quantitatively even in the presence of noise.

Distributed representations of graphs for drug pair scoring

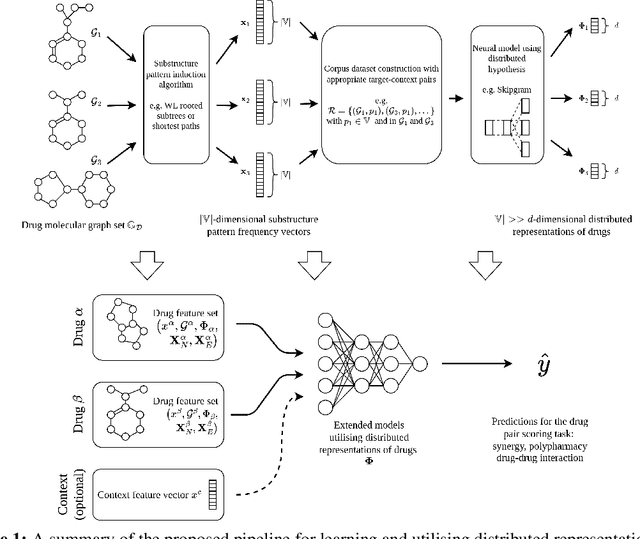
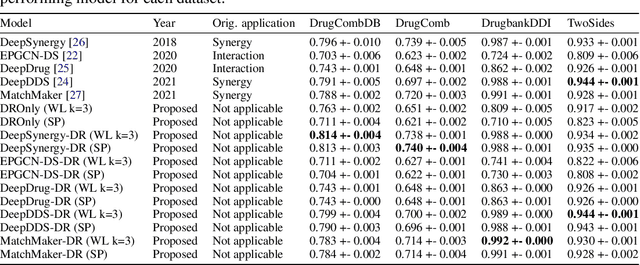
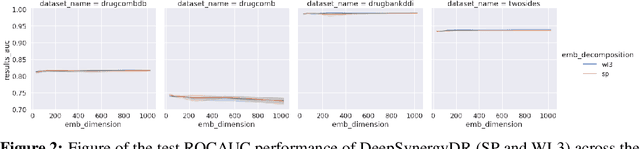
In this paper we study the practicality and usefulness of incorporating distributed representations of graphs into models within the context of drug pair scoring. We argue that the real world growth and update cycles of drug pair scoring datasets subvert the limitations of transductive learning associated with distributed representations. Furthermore, we argue that the vocabulary of discrete substructure patterns induced over drug sets is not dramatically large due to the limited set of atom types and constraints on bonding patterns enforced by chemistry. Under this pretext, we explore the effectiveness of distributed representations of the molecular graphs of drugs in drug pair scoring tasks such as drug synergy, polypharmacy, and drug-drug interaction prediction. To achieve this, we present a methodology for learning and incorporating distributed representations of graphs within a unified framework for drug pair scoring. Subsequently, we augment a number of recent and state-of-the-art models to utilise our embeddings. We empirically show that the incorporation of these embeddings improves downstream performance of almost every model across different drug pair scoring tasks, even those the original model was not designed for. We publicly release all of our drug embeddings for the DrugCombDB, DrugComb, DrugbankDDI, and TwoSides datasets.

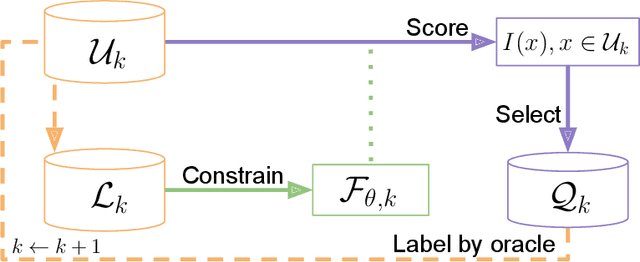
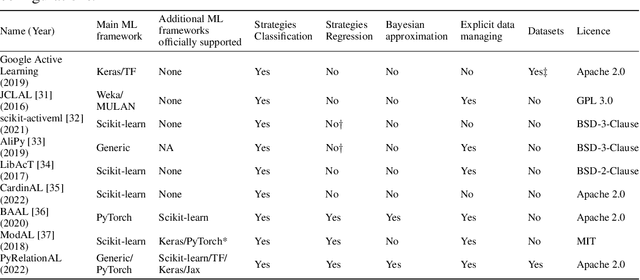
PyRelationAL: A Library for Active Learning Research and Development

In constrained real-world scenarios where it is challenging or costly to generate data, disciplined methods for acquiring informative new data points are of fundamental importance for the efficient training of machine learning (ML) models. Active learning (AL) is a subfield of ML focused on the development of methods to iteratively and economically acquire data through strategically querying new data points that are the most useful for a particular task. Here, we introduce PyRelationAL, an open source library for AL research. We describe a modular toolkit that is compatible with diverse ML frameworks (e.g. PyTorch, Scikit-Learn, TensorFlow, JAX). Furthermore, to help accelerate research and development in the field, the library implements a number of published methods and provides API access to wide-ranging benchmark datasets and AL task configurations based on existing literature. The library is supplemented by an expansive set of tutorials, demos, and documentation to help users get started. We perform experiments on the PyRelationAL collection of benchmark datasets and showcase the considerable economies that AL can provide. PyRelationAL is maintained using modern software engineering practices - with an inclusive contributor code of conduct - to promote long term library quality and utilisation.

PyTorch Geometric Temporal: Spatiotemporal Signal Processing with Neural Machine Learning Models

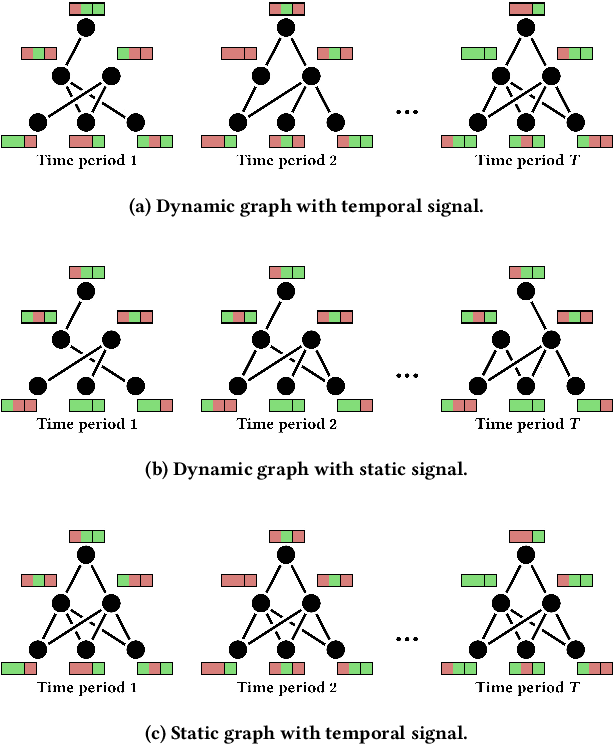
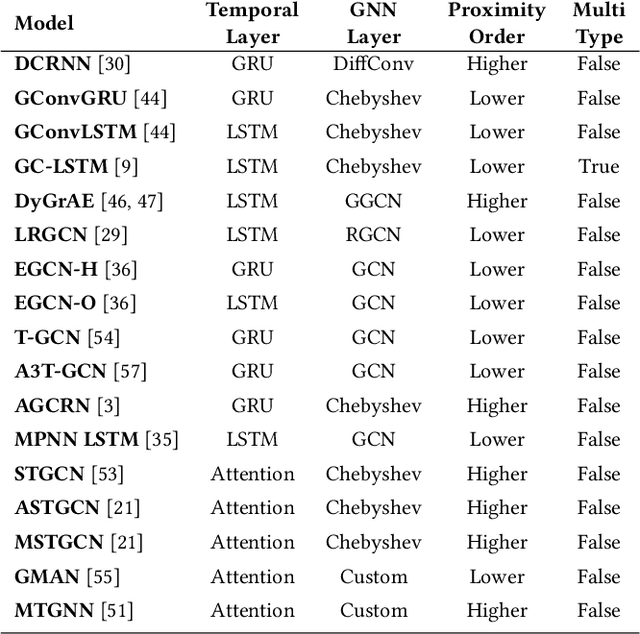
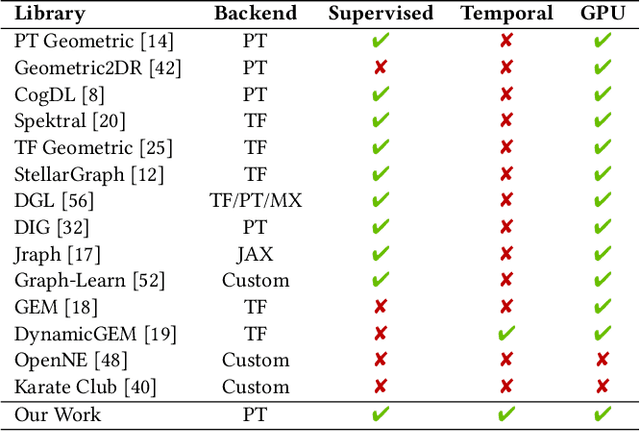
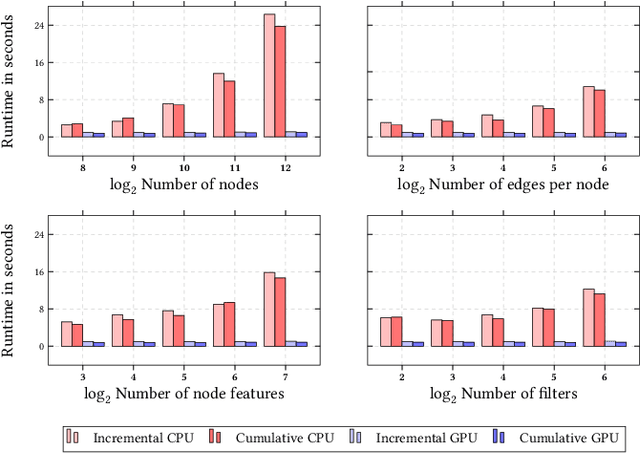
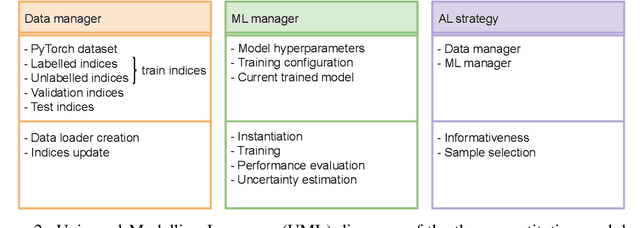
We present PyTorch Geometric Temporal a deep learning framework combining state-of-the-art machine learning algorithms for neural spatiotemporal signal processing. The main goal of the library is to make temporal geometric deep learning available for researchers and machine learning practitioners in a unified easy-to-use framework. PyTorch Geometric Temporal was created with foundations on existing libraries in the PyTorch eco-system, streamlined neural network layer definitions, temporal snapshot generators for batching, and integrated benchmark datasets. These features are illustrated with a tutorial-like case study. Experiments demonstrate the predictive performance of the models implemented in the library on real world problems such as epidemiological forecasting, ridehail demand prediction and web-traffic management. Our sensitivity analysis of runtime shows that the framework can potentially operate on web-scale datasets with rich temporal features and spatial structure.

Chickenpox Cases in Hungary: a Benchmark Dataset for Spatiotemporal Signal Processing with Graph Neural Networks

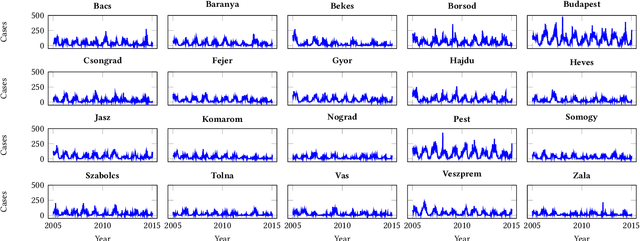
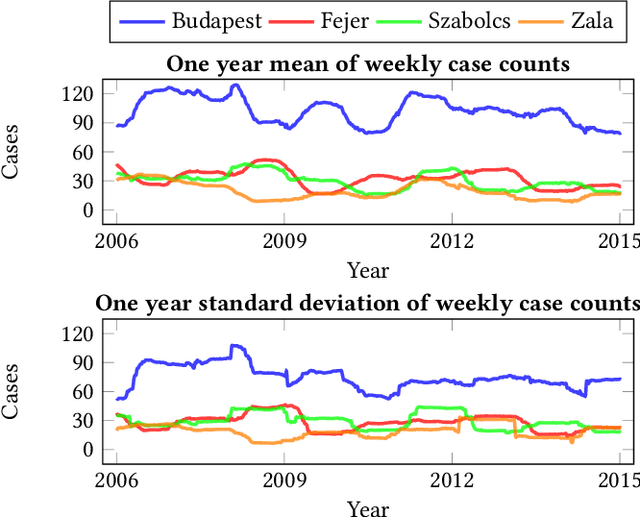
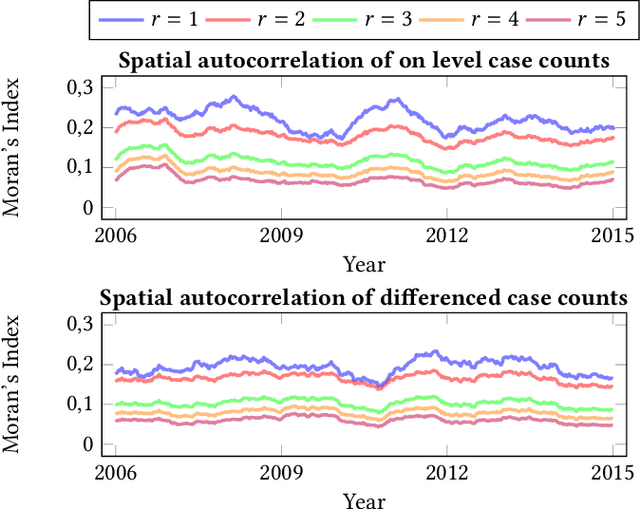
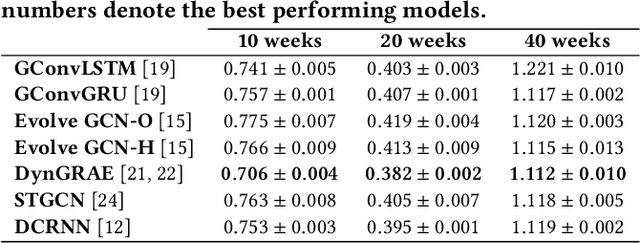
Recurrent graph convolutional neural networks are highly effective machine learning techniques for spatiotemporal signal processing. Newly proposed graph neural network architectures are repetitively evaluated on standard tasks such as traffic or weather forecasting. In this paper, we propose the Chickenpox Cases in Hungary dataset as a new dataset for comparing graph neural network architectures. Our time series analysis and forecasting experiments demonstrate that the Chickenpox Cases in Hungary dataset is adequate for comparing the predictive performance and forecasting capabilities of novel recurrent graph neural network architectures.

Using ontology embeddings for structural inductive bias in gene expression data analysis

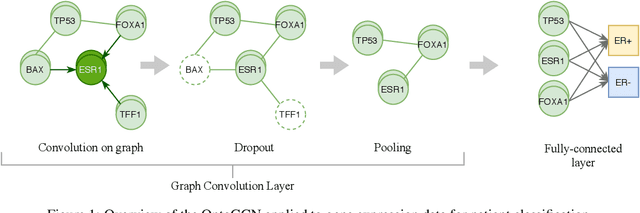
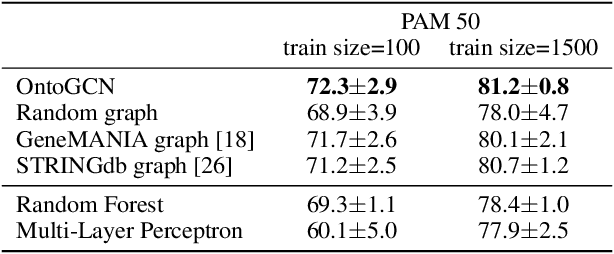
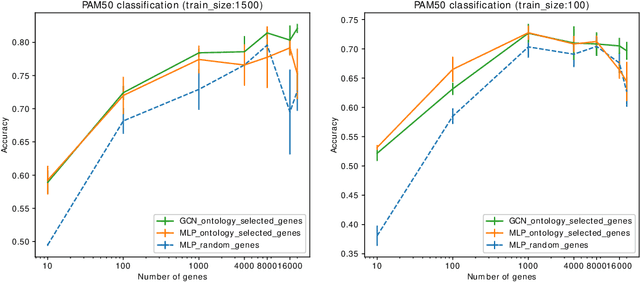
Stratifying cancer patients based on their gene expression levels allows improving diagnosis, survival analysis and treatment planning. However, such data is extremely highly dimensional as it contains expression values for over 20000 genes per patient, and the number of samples in the datasets is low. To deal with such settings, we propose to incorporate prior biological knowledge about genes from ontologies into the machine learning system for the task of patient classification given their gene expression data. We use ontology embeddings that capture the semantic similarities between the genes to direct a Graph Convolutional Network, and therefore sparsify the network connections. We show this approach provides an advantage for predicting clinical targets from high-dimensional low-sample data.

Incorporating network based protein complex discovery into automated model construction

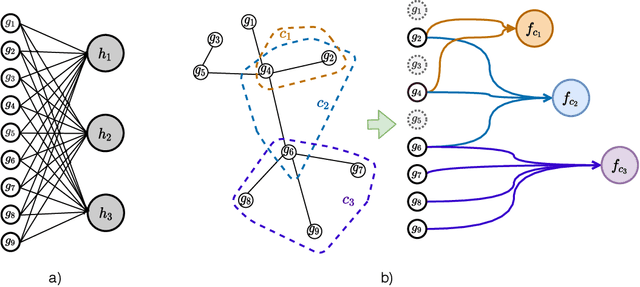
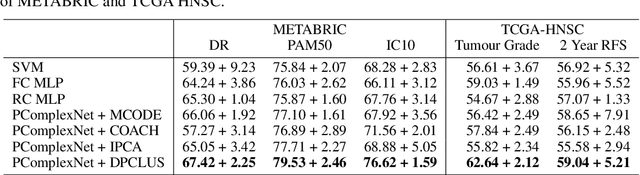
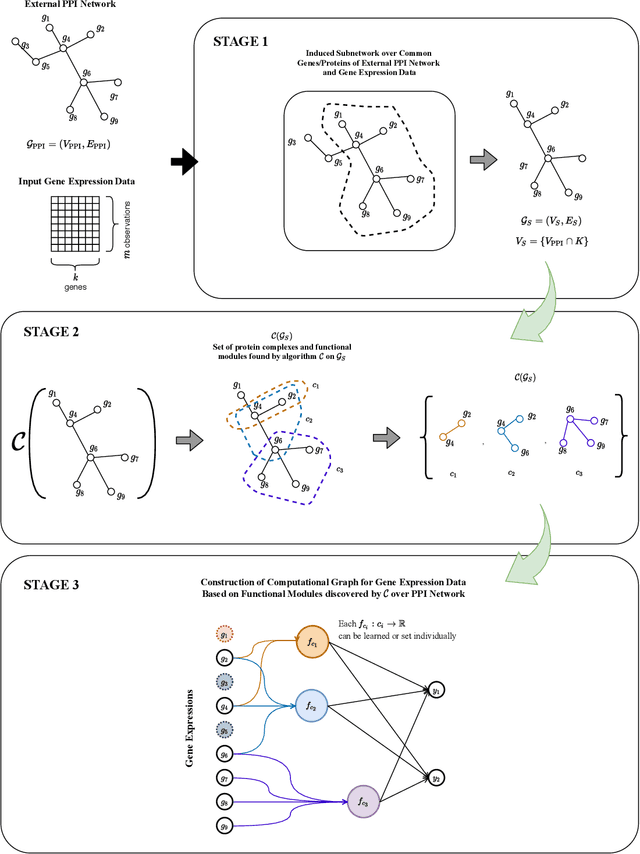
We propose a method for gene expression based analysis of cancer phenotypes incorporating network biology knowledge through unsupervised construction of computational graphs. The structural construction of the computational graphs is driven by the use of topological clustering algorithms on protein-protein networks which incorporate inductive biases stemming from network biology research in protein complex discovery. This structurally constrains the hypothesis space over the possible computational graph factorisation whose parameters can then be learned through supervised or unsupervised task settings. The sparse construction of the computational graph enables the differential protein complex activity analysis whilst also interpreting the individual contributions of genes/proteins involved in each individual protein complex. In our experiments analysing a variety of cancer phenotypes, we show that the proposed methods outperform SVM, Fully-Connected MLP, and Randomly-Connected MLPs in all tasks. Our work introduces a scalable method for incorporating large interaction networks as prior knowledge to drive the construction of powerful computational models amenable to introspective study.

Learning distributed representations of graphs with Geo2DR

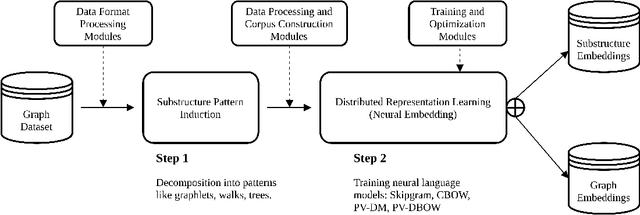
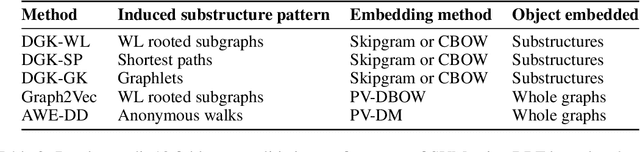
We present Geo2DR, a Python library for unsupervised learning on graph-structured data using discrete substructure patterns and neural language models. It contains efficient implementations of popular graph decomposition algorithms and neural language models in PyTorch which are combined to learn representations using the distributive hypothesis. Furthermore, Geo2DR comes with general data processing and loading methods which can bring substantial speed-up in the training of the neural language models. Through this we provide a unified set of tools and design methodology to quickly construct systems capable of learning distributed representations of graphs. This is useful for replication of existing methods, modification, or even creation of novel systems. This work serves to present the Geo2DR library and perform a comprehensive comparative analysis of existing methods re-implemented using Geo2DR across several widely used graph classification benchmarks. We show a high reproducibility of results in published methods and interoperability with other libraries useful for distributive language modelling.

Decoupling feature propagation from the design of graph auto-encoders

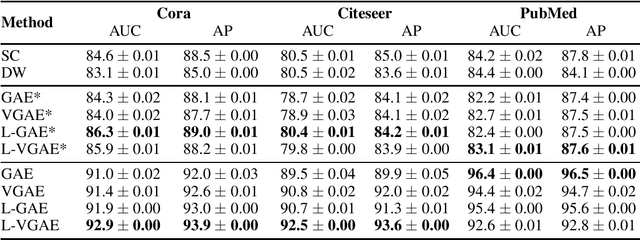
We present two instances, L-GAE and L-VGAE, of the variational graph auto-encoding family (VGAE) based on separating feature propagation operations from graph convolution layers typically found in graph learning methods to a single linear matrix computation made prior to input in standard auto-encoder architectures. This decoupling enables the independent and fixed design of the auto-encoder without requiring additional GCN layers for every desired increase in the size of a node's local receptive field. Fixing the auto-encoder enables a fairer assessment on the size of a nodes receptive field in building representations. Furthermore a by-product of fixing the auto-encoder design often results in substantially smaller networks than their VGAE counterparts especially as we increase the number of feature propagations. A comparative downstream evaluation on link prediction tasks show comparable state of the art performance to similar VGAE arrangements despite considerable simplification. We also show the simple application of our methodology to more challenging representation learning scenarios such as spatio-temporal graph representation learning.