Alison Pouplin
Spacetime Geometry of Denoising in Diffusion Models
May 23, 2025Abstract:We present a novel perspective on diffusion models using the framework of information geometry. We show that the set of noisy samples, taken across all noise levels simultaneously, forms a statistical manifold -- a family of denoising probability distributions. Interpreting the noise level as a temporal parameter, we refer to this manifold as spacetime. This manifold naturally carries a Fisher-Rao metric, which defines geodesics -- shortest paths between noisy points. Notably, this family of distributions is exponential, enabling efficient geodesic computation even in high-dimensional settings without retraining or fine-tuning. We demonstrate the practical value of this geometric viewpoint in transition path sampling, where spacetime geodesics define smooth sequences of Boltzmann distributions, enabling the generation of continuous trajectories between low-energy metastable states. Code is available at: https://github.com/Aalto-QuML/diffusion-spacetime-geometry.
Towards Variational Flow Matching on General Geometries
Feb 18, 2025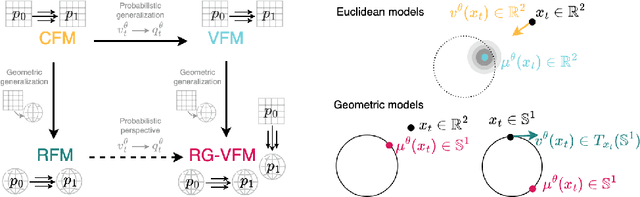


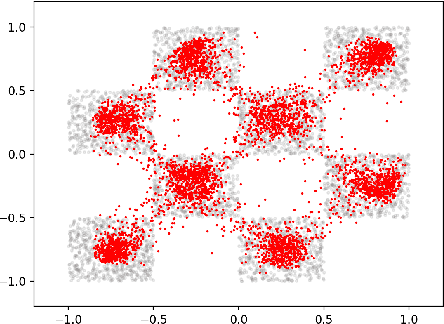
Abstract:We introduce Riemannian Gaussian Variational Flow Matching (RG-VFM), an extension of Variational Flow Matching (VFM) that leverages Riemannian Gaussian distributions for generative modeling on structured manifolds. We derive a variational objective for probability flows on manifolds with closed-form geodesics, making RG-VFM comparable - though fundamentally different to Riemannian Flow Matching (RFM) in this geometric setting. Experiments on a checkerboard dataset wrapped on the sphere demonstrate that RG-VFM captures geometric structure more effectively than Euclidean VFM and baseline methods, establishing it as a robust framework for manifold-aware generative modeling.
On the curvature of the loss landscape
Jul 10, 2023Abstract:One of the main challenges in modern deep learning is to understand why such over-parameterized models perform so well when trained on finite data. A way to analyze this generalization concept is through the properties of the associated loss landscape. In this work, we consider the loss landscape as an embedded Riemannian manifold and show that the differential geometric properties of the manifold can be used when analyzing the generalization abilities of a deep net. In particular, we focus on the scalar curvature, which can be computed analytically for our manifold, and show connections to several settings that potentially imply generalization.
Identifying latent distances with Finslerian geometry
Dec 20, 2022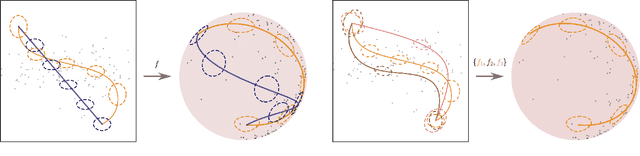

Abstract:Riemannian geometry provides powerful tools to explore the latent space of generative models while preserving the inherent structure of the data manifold. Lengths, energies and volume measures can be derived from a pullback metric, defined through the immersion that maps the latent space to the data space. With this in mind, most generative models are stochastic, and so is the pullback metric. Manipulating stochastic objects is strenuous in practice. In order to perform operations such as interpolations, or measuring the distance between data points, we need a deterministic approximation of the pullback metric. In this work, we are defining a new metric as the expected length derived from the stochastic pullback metric. We show this metric is Finslerian, and we compare it with the expected pullback metric. In high dimensions, we show that the metrics converge to each other at a rate of $\mathcal{O}\left(\frac{1}{D}\right)$.
PyRelationAL: A Library for Active Learning Research and Development
May 23, 2022
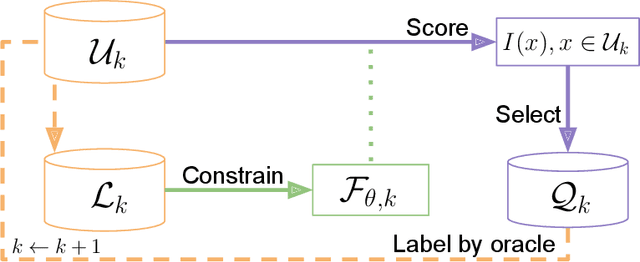
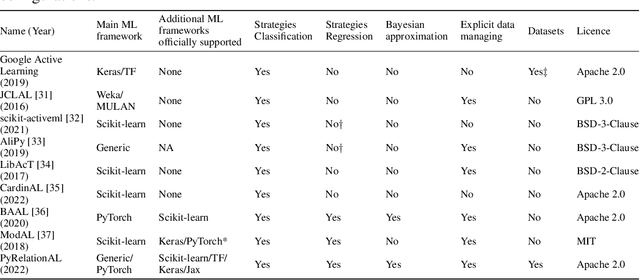
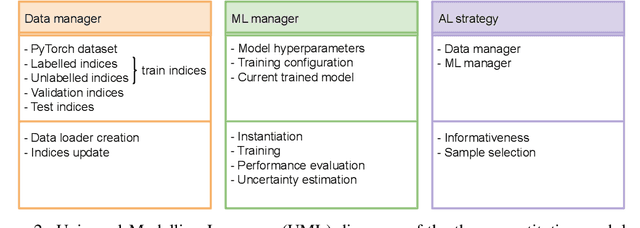
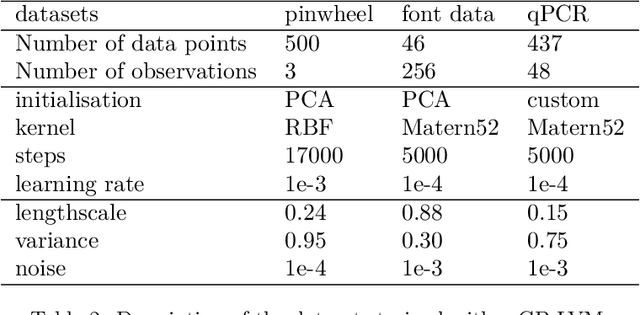
Abstract:In constrained real-world scenarios where it is challenging or costly to generate data, disciplined methods for acquiring informative new data points are of fundamental importance for the efficient training of machine learning (ML) models. Active learning (AL) is a subfield of ML focused on the development of methods to iteratively and economically acquire data through strategically querying new data points that are the most useful for a particular task. Here, we introduce PyRelationAL, an open source library for AL research. We describe a modular toolkit that is compatible with diverse ML frameworks (e.g. PyTorch, Scikit-Learn, TensorFlow, JAX). Furthermore, to help accelerate research and development in the field, the library implements a number of published methods and provides API access to wide-ranging benchmark datasets and AL task configurations based on existing literature. The library is supplemented by an expansive set of tutorials, demos, and documentation to help users get started. We perform experiments on the PyRelationAL collection of benchmark datasets and showcase the considerable economies that AL can provide. PyRelationAL is maintained using modern software engineering practices - with an inclusive contributor code of conduct - to promote long term library quality and utilisation.
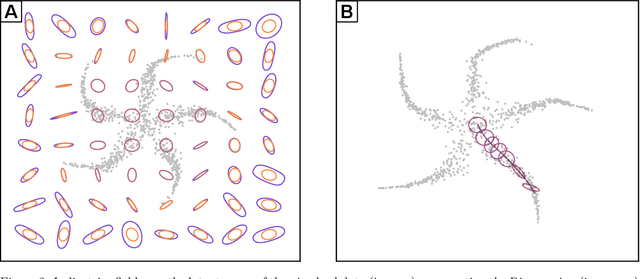
Pulling back information geometry
Jun 09, 2021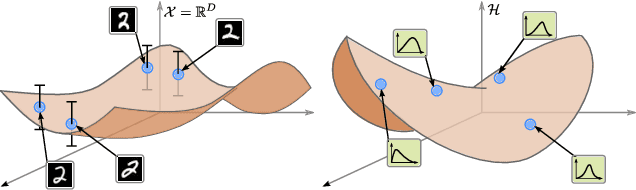

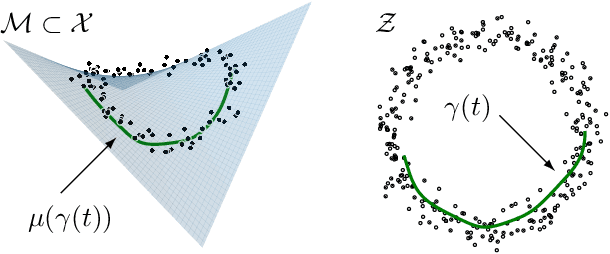

Abstract:Latent space geometry has shown itself to provide a rich and rigorous framework for interacting with the latent variables of deep generative models. The existing theory, however, relies on the decoder being a Gaussian distribution as its simple reparametrization allows us to interpret the generating process as a random projection of a deterministic manifold. Consequently, this approach breaks down when applied to decoders that are not as easily reparametrized. We here propose to use the Fisher-Rao metric associated with the space of decoder distributions as a reference metric, which we pull back to the latent space. We show that we can achieve meaningful latent geometries for a wide range of decoder distributions for which the previous theory was not applicable, opening the door to `black box' latent geometries.
Denoising Adversarial Autoencoders: Classifying Skin Lesions Using Limited Labelled Training Data
Jan 02, 2018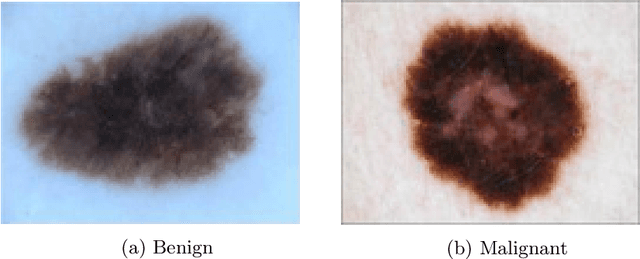

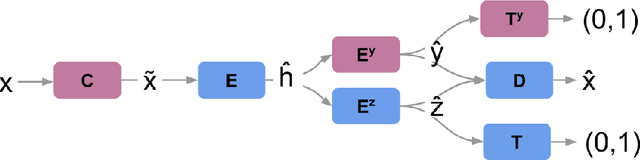

Abstract:We propose a novel deep learning model for classifying medical images in the setting where there is a large amount of unlabelled medical data available, but labelled data is in limited supply. We consider the specific case of classifying skin lesions as either malignant or benign. In this setting, the proposed approach -- the semi-supervised, denoising adversarial autoencoder -- is able to utilise vast amounts of unlabelled data to learn a representation for skin lesions, and small amounts of labelled data to assign class labels based on the learned representation. We analyse the contributions of both the adversarial and denoising components of the model and find that the combination yields superior classification performance in the setting of limited labelled training data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge