Dimitris Kalatzis
Controllable 3D Placement of Objects with Scene-Aware Diffusion Models
Jun 26, 2025Abstract:Image editing approaches have become more powerful and flexible with the advent of powerful text-conditioned generative models. However, placing objects in an environment with a precise location and orientation still remains a challenge, as this typically requires carefully crafted inpainting masks or prompts. In this work, we show that a carefully designed visual map, combined with coarse object masks, is sufficient for high quality object placement. We design a conditioning signal that resolves ambiguities, while being flexible enough to allow for changing of shapes or object orientations. By building on an inpainting model, we leave the background intact by design, in contrast to methods that model objects and background jointly. We demonstrate the effectiveness of our method in the automotive setting, where we compare different conditioning signals in novel object placement tasks. These tasks are designed to measure edit quality not only in terms of appearance, but also in terms of pose and location accuracy, including cases that require non-trivial shape changes. Lastly, we show that fine location control can be combined with appearance control to place existing objects in precise locations in a scene.
Gaussian Splatting is an Effective Data Generator for 3D Object Detection
Apr 23, 2025



Abstract:We investigate data augmentation for 3D object detection in autonomous driving. We utilize recent advancements in 3D reconstruction based on Gaussian Splatting for 3D object placement in driving scenes. Unlike existing diffusion-based methods that synthesize images conditioned on BEV layouts, our approach places 3D objects directly in the reconstructed 3D space with explicitly imposed geometric transformations. This ensures both the physical plausibility of object placement and highly accurate 3D pose and position annotations. Our experiments demonstrate that even by integrating a limited number of external 3D objects into real scenes, the augmented data significantly enhances 3D object detection performance and outperforms existing diffusion-based 3D augmentation for object detection. Extensive testing on the nuScenes dataset reveals that imposing high geometric diversity in object placement has a greater impact compared to the appearance diversity of objects. Additionally, we show that generating hard examples, either by maximizing detection loss or imposing high visual occlusion in camera images, does not lead to more efficient 3D data augmentation for camera-based 3D object detection in autonomous driving.
MobileNVC: Real-time 1080p Neural Video Compression on a Mobile Device
Oct 02, 2023



Abstract:Neural video codecs have recently become competitive with standard codecs such as HEVC in the low-delay setting. However, most neural codecs are large floating-point networks that use pixel-dense warping operations for temporal modeling, making them too computationally expensive for deployment on mobile devices. Recent work has demonstrated that running a neural decoder in real time on mobile is feasible, but shows this only for 720p RGB video, while the YUV420 format is more commonly used in production. This work presents the first neural video codec that decodes 1080p YUV420 video in real time on a mobile device. Our codec relies on two major contributions. First, we design an efficient codec that uses a block-based motion compensation algorithm available on the warping core of the mobile accelerator, and we show how to quantize this model to integer precision. Second, we implement a fast decoder pipeline that concurrently runs neural network components on the neural signal processor, parallel entropy coding on the mobile GPU, and warping on the warping core. Our codec outperforms the previous on-device codec by a large margin with up to 48 % BD-rate savings, while reducing the MAC count on the receiver side by 10x. We perform a careful ablation to demonstrate the effect of the introduced motion compensation scheme, and ablate the effect of model quantization.
Pulling back information geometry
Jun 09, 2021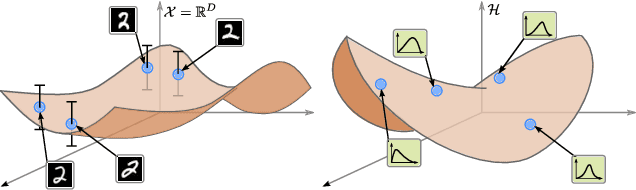


Abstract:Latent space geometry has shown itself to provide a rich and rigorous framework for interacting with the latent variables of deep generative models. The existing theory, however, relies on the decoder being a Gaussian distribution as its simple reparametrization allows us to interpret the generating process as a random projection of a deterministic manifold. Consequently, this approach breaks down when applied to decoders that are not as easily reparametrized. We here propose to use the Fisher-Rao metric associated with the space of decoder distributions as a reference metric, which we pull back to the latent space. We show that we can achieve meaningful latent geometries for a wide range of decoder distributions for which the previous theory was not applicable, opening the door to `black box' latent geometries.
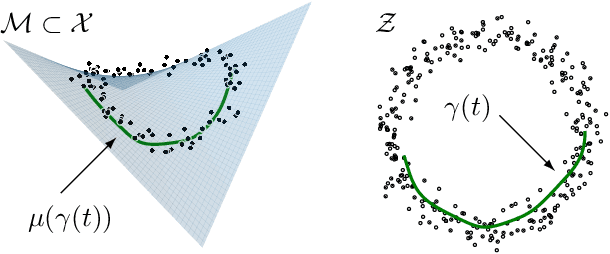
Multi-chart flows
Jun 07, 2021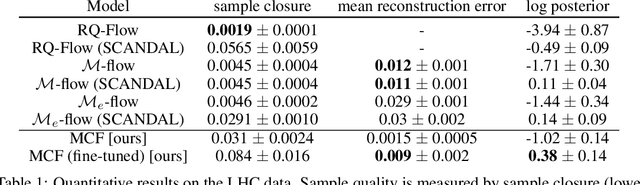
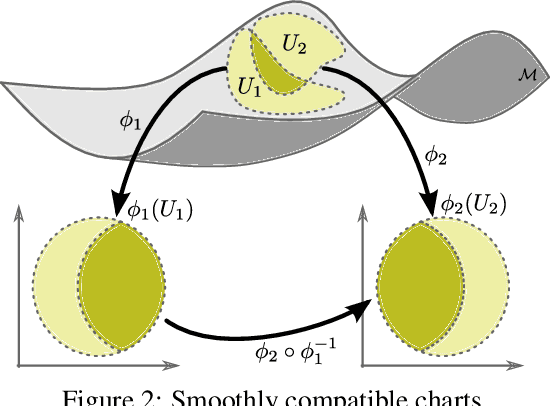
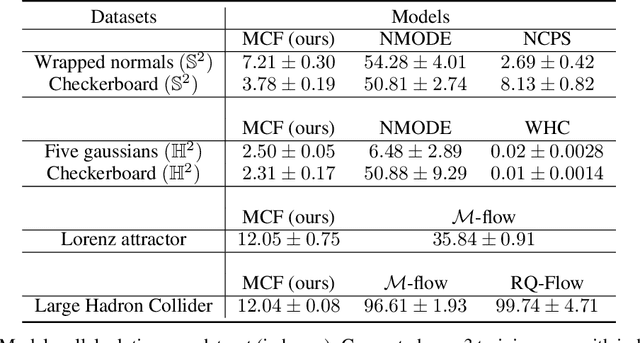
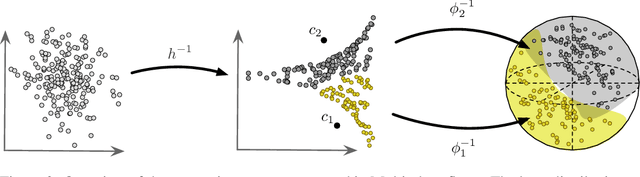
Abstract:We present Multi-chart flows, a flow-based model for concurrently learning topologically non-trivial manifolds and statistical densities on them. Current methods focus on manifolds that are topologically Euclidean, enforce strong structural priors on the learned models or use operations that do not scale to high dimensions. In contrast, our model learns the local manifold topology piecewise by "gluing" it back together through a collection of learned coordinate charts. We demonstrate the efficiency of our approach on synthetic data of known manifolds, as well as higher dimensional manifolds of unknown topology, where we show better sample efficiency and competitive or superior performance against current state-of-the-art.
Variational Autoencoders with Riemannian Brownian Motion Priors
Feb 18, 2020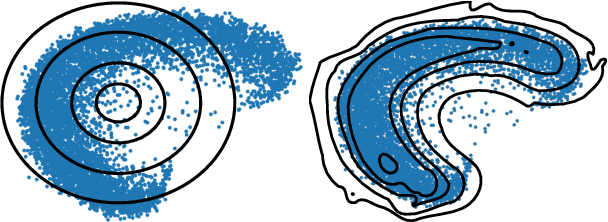


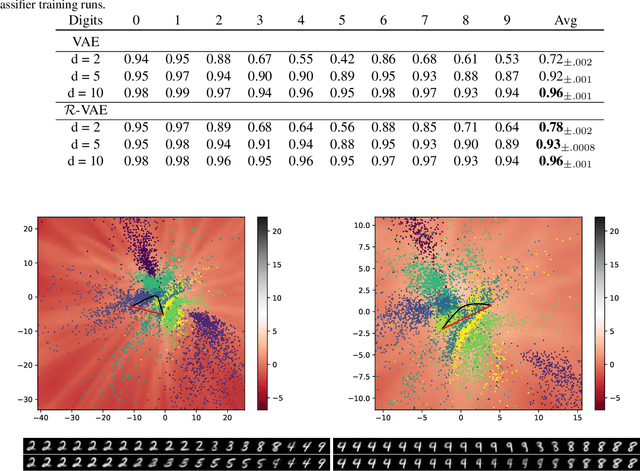
Abstract:Variational Autoencoders (VAEs) represent the given data in a low-dimensional latent space, which is generally assumed to be Euclidean. This assumption naturally leads to the common choice of a standard Gaussian prior over continuous latent variables. Recent work has, however, shown that this prior has a detrimental effect on model capacity, leading to subpar performance. We propose that the Euclidean assumption lies at the heart of this failure mode. To counter this, we assume a Riemannian structure over the latent space, which constitutes a more principled geometric view of the latent codes, and replace the standard Gaussian prior with a Riemannian Brownian motion prior. We propose an efficient inference scheme that does not rely on the unknown normalizing factor of this prior. Finally, we demonstrate that this prior significantly increases model capacity using only one additional scalar parameter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge