Variational Point Encoding Deformation for Dental Modeling

Digital dentistry has made significant advancements in recent years, yet numerous challenges remain to be addressed. In this study, we release a new extensive dataset of tooth meshes to encourage further research. Additionally, we propose Variational FoldingNet (VF-Net), which extends FoldingNet to enable probabilistic learning of point cloud representations. A key challenge in existing latent variable models for point clouds is the lack of a 1-to-1 mapping between input points and output points. Instead, they must rely on optimizing Chamfer distances, a metric that does not have a normalized distributional counterpart, preventing its usage in probabilistic models. We demonstrate that explicit minimization of Chamfer distances can be replaced by a suitable encoder, which allows us to increase computational efficiency while simplifying the probabilistic extension. Our experimental findings present empirical evidence demonstrating the superior performance of VF-Net over existing models in terms of dental scan reconstruction and extrapolation. Additionally, our investigation highlights the robustness of VF-Net's latent representations. These results underscore the promising prospects of VF-Net as an effective and reliable method for point cloud reconstruction and analysis.

Multi-chart flows

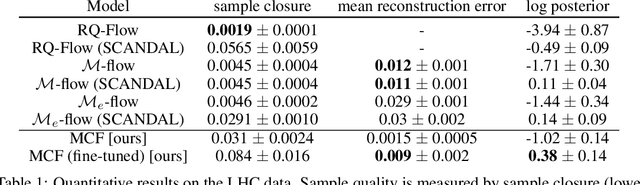
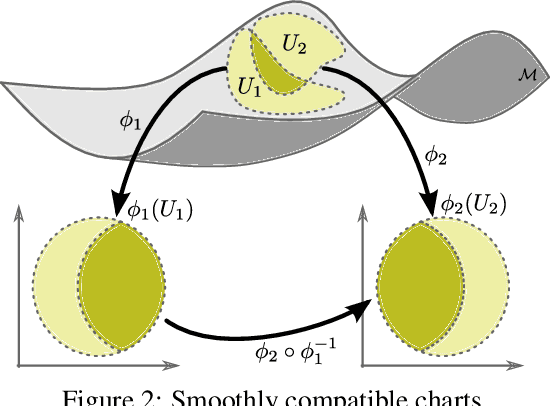
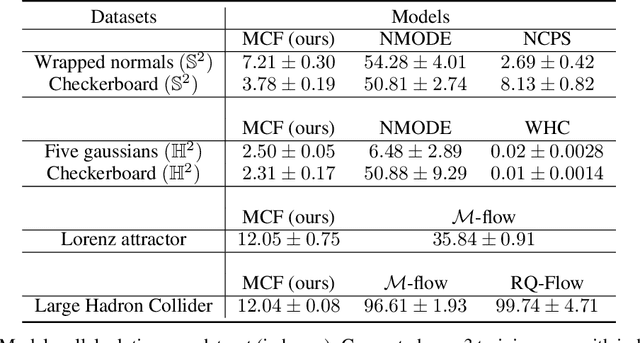
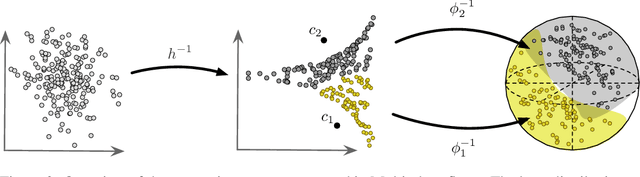
We present Multi-chart flows, a flow-based model for concurrently learning topologically non-trivial manifolds and statistical densities on them. Current methods focus on manifolds that are topologically Euclidean, enforce strong structural priors on the learned models or use operations that do not scale to high dimensions. In contrast, our model learns the local manifold topology piecewise by "gluing" it back together through a collection of learned coordinate charts. We demonstrate the efficiency of our approach on synthetic data of known manifolds, as well as higher dimensional manifolds of unknown topology, where we show better sample efficiency and competitive or superior performance against current state-of-the-art.