Multi-chart flows

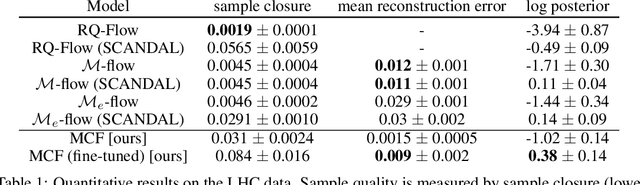
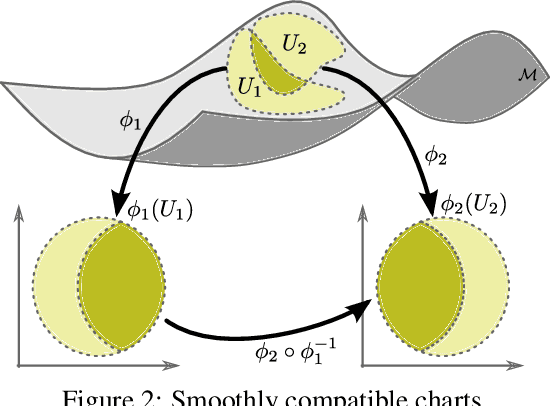
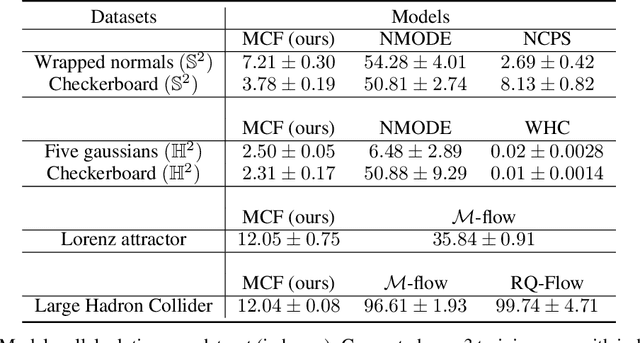
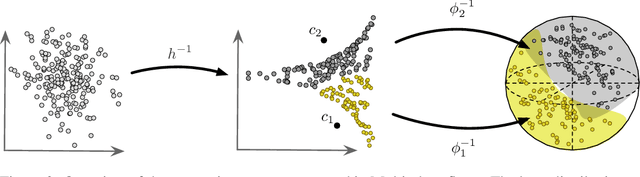
We present Multi-chart flows, a flow-based model for concurrently learning topologically non-trivial manifolds and statistical densities on them. Current methods focus on manifolds that are topologically Euclidean, enforce strong structural priors on the learned models or use operations that do not scale to high dimensions. In contrast, our model learns the local manifold topology piecewise by "gluing" it back together through a collection of learned coordinate charts. We demonstrate the efficiency of our approach on synthetic data of known manifolds, as well as higher dimensional manifolds of unknown topology, where we show better sample efficiency and competitive or superior performance against current state-of-the-art.