Exploring bidirectional bounds for minimax-training of Energy-based models

Energy-based models (EBMs) estimate unnormalized densities in an elegant framework, but they are generally difficult to train. Recent work has linked EBMs to generative adversarial networks, by noting that they can be trained through a minimax game using a variational lower bound. To avoid the instabilities caused by minimizing a lower bound, we propose to instead work with bidirectional bounds, meaning that we maximize a lower bound and minimize an upper bound when training the EBM. We investigate four different bounds on the log-likelihood derived from different perspectives. We derive lower bounds based on the singular values of the generator Jacobian and on mutual information. To upper bound the negative log-likelihood, we consider a gradient penalty-like bound, as well as one based on diffusion processes. In all cases, we provide algorithms for evaluating the bounds. We compare the different bounds to investigate, the pros and cons of the different approaches. Finally, we demonstrate that the use of bidirectional bounds stabilizes EBM training and yields high-quality density estimation and sample generation.

Learning geometry and topology via multi-chart flows

Real world data often lie on low-dimensional Riemannian manifolds embedded in high-dimensional spaces. This motivates learning degenerate normalizing flows that map between the ambient space and a low-dimensional latent space. However, if the manifold has a non-trivial topology, it can never be correctly learned using a single flow. Instead multiple flows must be `glued together'. In this paper, we first propose the general training scheme for learning such a collection of flows, and secondly we develop the first numerical algorithms for computing geodesics on such manifolds. Empirically, we demonstrate that this leads to highly significant improvements in topology estimation.

Spacetime Geometry of Denoising in Diffusion Models

We present a novel perspective on diffusion models using the framework of information geometry. We show that the set of noisy samples, taken across all noise levels simultaneously, forms a statistical manifold -- a family of denoising probability distributions. Interpreting the noise level as a temporal parameter, we refer to this manifold as spacetime. This manifold naturally carries a Fisher-Rao metric, which defines geodesics -- shortest paths between noisy points. Notably, this family of distributions is exponential, enabling efficient geodesic computation even in high-dimensional settings without retraining or fine-tuning. We demonstrate the practical value of this geometric viewpoint in transition path sampling, where spacetime geodesics define smooth sequences of Boltzmann distributions, enabling the generation of continuous trajectories between low-energy metastable states. Code is available at: https://github.com/Aalto-QuML/diffusion-spacetime-geometry.

Riemann$^2$: Learning Riemannian Submanifolds from Riemannian Data

Latent variable models are powerful tools for learning low-dimensional manifolds from high-dimensional data. However, when dealing with constrained data such as unit-norm vectors or symmetric positive-definite matrices, existing approaches ignore the underlying geometric constraints or fail to provide meaningful metrics in the latent space. To address these limitations, we propose to learn Riemannian latent representations of such geometric data. To do so, we estimate the pullback metric induced by a Wrapped Gaussian Process Latent Variable Model, which explicitly accounts for the data geometry. This enables us to define geometry-aware notions of distance and shortest paths in the latent space, while ensuring that our model only assigns probability mass to the data manifold. This generalizes previous work and allows us to handle complex tasks in various domains, including robot motion synthesis and analysis of brain connectomes.

Identifying metric structures of deep latent variable models

Deep latent variable models learn condensed representations of data that, hopefully, reflect the inner workings of the studied phenomena. Unfortunately, these latent representations are not statistically identifiable, meaning they cannot be uniquely determined. Domain experts, therefore, need to tread carefully when interpreting these. Current solutions limit the lack of identifiability through additional constraints on the latent variable model, e.g. by requiring labeled training data, or by restricting the expressivity of the model. We change the goal: instead of identifying the latent variables, we identify relationships between them such as meaningful distances, angles, and volumes. We prove this is feasible under very mild model conditions and without additional labeled data. We empirically demonstrate that our theory results in more reliable latent distances, offering a principled path forward in extracting trustworthy conclusions from deep latent variable models.

Are generative models fair? A study of racial bias in dermatological image generation

Racial bias in medicine, particularly in dermatology, presents significant ethical and clinical challenges. It often results from the underrepresentation of darker skin tones in training datasets for machine learning models. While efforts to address bias in dermatology have focused on improving dataset diversity and mitigating disparities in discriminative models, the impact of racial bias on generative models remains underexplored. Generative models, such as Variational Autoencoders (VAEs), are increasingly used in healthcare applications, yet their fairness across diverse skin tones is currently not well understood. In this study, we evaluate the fairness of generative models in clinical dermatology with respect to racial bias. For this purpose, we first train a VAE with a perceptual loss to generate and reconstruct high-quality skin images across different skin tones. We utilize the Fitzpatrick17k dataset to examine how racial bias influences the representation and performance of these models. Our findings indicate that the VAE is influenced by the diversity of skin tones in the training dataset, with better performance observed for lighter skin tones. Additionally, the uncertainty estimates produced by the VAE are ineffective in assessing the model's fairness. These results highlight the need for improved uncertainty quantification mechanisms to detect and address racial bias in generative models for trustworthy healthcare technologies.

Extended Neural Contractive Dynamical Systems: On Multiple Tasks and Riemannian Safety Regions

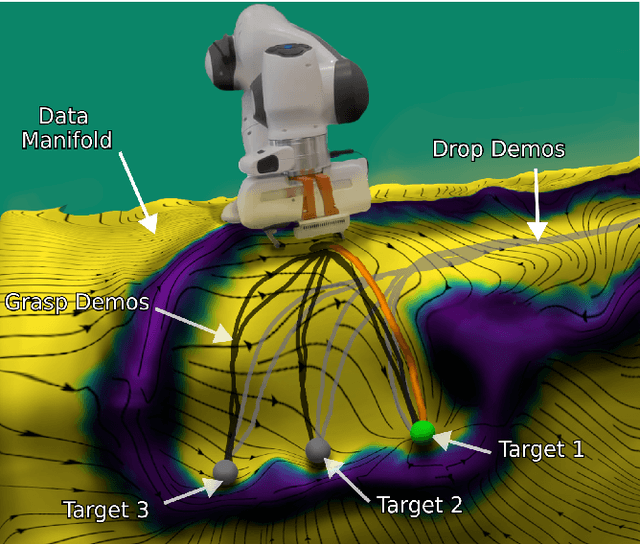
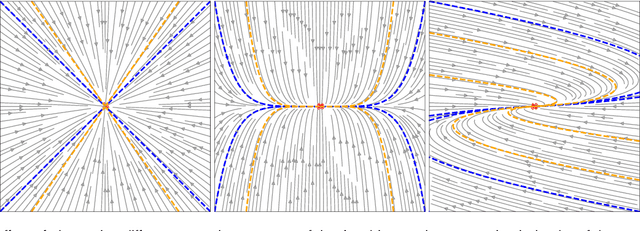
Stability guarantees are crucial when ensuring that a fully autonomous robot does not take undesirable or potentially harmful actions. We recently proposed the Neural Contractive Dynamical Systems (NCDS), which is a neural network architecture that guarantees contractive stability. With this, learning-from-demonstrations approaches can trivially provide stability guarantees. However, our early work left several unanswered questions, which we here address. Beyond providing an in-depth explanation of NCDS, this paper extends the framework with more careful regularization, a conditional variant of the framework for handling multiple tasks, and an uncertainty-driven approach to latent obstacle avoidance. Experiments verify that the developed system has the flexibility of ordinary neural networks while providing the stability guarantees needed for autonomous robotics.

Bayes without Underfitting: Fully Correlated Deep Learning Posteriors via Alternating Projections

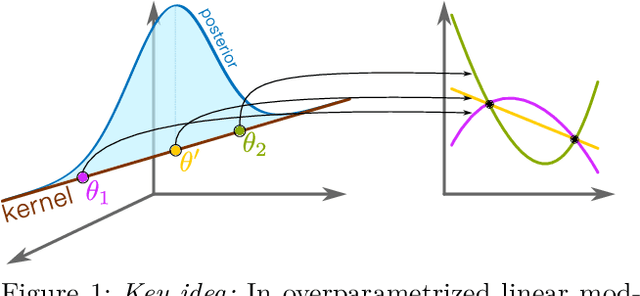
Bayesian deep learning all too often underfits so that the Bayesian prediction is less accurate than a simple point estimate. Uncertainty quantification then comes at the cost of accuracy. For linearized models, the null space of the generalized Gauss-Newton matrix corresponds to parameters that preserve the training predictions of the point estimate. We propose to build Bayesian approximations in this null space, thereby guaranteeing that the Bayesian predictive does not underfit. We suggest a matrix-free algorithm for projecting onto this null space, which scales linearly with the number of parameters and quadratically with the number of output dimensions. We further propose an approximation that only scales linearly with parameters to make the method applicable to generative models. An extensive empirical evaluation shows that the approach scales to large models, including vision transformers with 28 million parameters.

Decoder ensembling for learned latent geometries

Latent space geometry provides a rigorous and empirically valuable framework for interacting with the latent variables of deep generative models. This approach reinterprets Euclidean latent spaces as Riemannian through a pull-back metric, allowing for a standard differential geometric analysis of the latent space. Unfortunately, data manifolds are generally compact and easily disconnected or filled with holes, suggesting a topological mismatch to the Euclidean latent space. The most established solution to this mismatch is to let uncertainty be a proxy for topology, but in neural network models, this is often realized through crude heuristics that lack principle and generally do not scale to high-dimensional representations. We propose using ensembles of decoders to capture model uncertainty and show how to easily compute geodesics on the associated expected manifold. Empirically, we find this simple and reliable, thereby coming one step closer to easy-to-use latent geometries.

A survey and benchmark of high-dimensional Bayesian optimization of discrete sequences

Optimizing discrete black-box functions is key in several domains, e.g. protein engineering and drug design. Due to the lack of gradient information and the need for sample efficiency, Bayesian optimization is an ideal candidate for these tasks. Several methods for high-dimensional continuous and categorical Bayesian optimization have been proposed recently. However, our survey of the field reveals highly heterogeneous experimental set-ups across methods and technical barriers for the replicability and application of published algorithms to real-world tasks. To address these issues, we develop a unified framework to test a vast array of high-dimensional Bayesian optimization methods and a collection of standardized black-box functions representing real-world application domains in chemistry and biology. These two components of the benchmark are each supported by flexible, scalable, and easily extendable software libraries (poli and poli-baselines), allowing practitioners to readily incorporate new optimization objectives or discrete optimizers. Project website: https://machinelearninglifescience.github.io/hdbo_benchmark