Bayes without Underfitting: Fully Correlated Deep Learning Posteriors via Alternating Projections

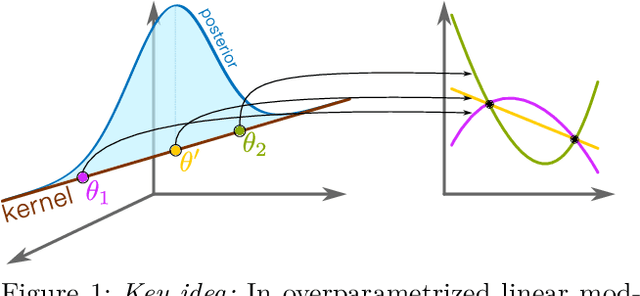
Bayesian deep learning all too often underfits so that the Bayesian prediction is less accurate than a simple point estimate. Uncertainty quantification then comes at the cost of accuracy. For linearized models, the null space of the generalized Gauss-Newton matrix corresponds to parameters that preserve the training predictions of the point estimate. We propose to build Bayesian approximations in this null space, thereby guaranteeing that the Bayesian predictive does not underfit. We suggest a matrix-free algorithm for projecting onto this null space, which scales linearly with the number of parameters and quadratically with the number of output dimensions. We further propose an approximation that only scales linearly with parameters to make the method applicable to generative models. An extensive empirical evaluation shows that the approach scales to large models, including vision transformers with 28 million parameters.

Reparameterization invariance in approximate Bayesian inference

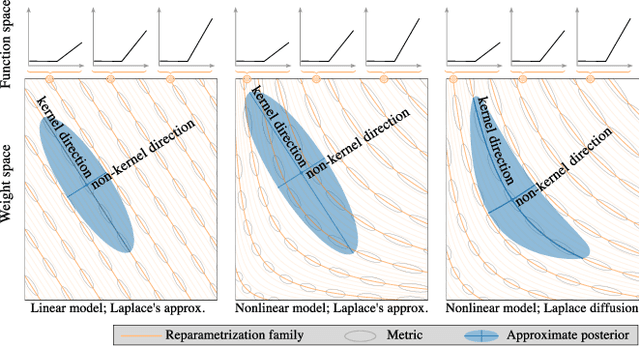
Current approximate posteriors in Bayesian neural networks (BNNs) exhibit a crucial limitation: they fail to maintain invariance under reparameterization, i.e. BNNs assign different posterior densities to different parametrizations of identical functions. This creates a fundamental flaw in the application of Bayesian principles as it breaks the correspondence between uncertainty over the parameters with uncertainty over the parametrized function. In this paper, we investigate this issue in the context of the increasingly popular linearized Laplace approximation. Specifically, it has been observed that linearized predictives alleviate the common underfitting problems of the Laplace approximation. We develop a new geometric view of reparametrizations from which we explain the success of linearization. Moreover, we demonstrate that these reparameterization invariance properties can be extended to the original neural network predictive using a Riemannian diffusion process giving a straightforward algorithm for approximate posterior sampling, which empirically improves posterior fit.

Laplacian Segmentation Networks: Improved Epistemic Uncertainty from Spatial Aleatoric Uncertainty

Out of distribution (OOD) medical images are frequently encountered, e.g. because of site- or scanner differences, or image corruption. OOD images come with a risk of incorrect image segmentation, potentially negatively affecting downstream diagnoses or treatment. To ensure robustness to such incorrect segmentations, we propose Laplacian Segmentation Networks (LSN) that jointly model epistemic (model) and aleatoric (data) uncertainty in image segmentation. We capture data uncertainty with a spatially correlated logit distribution. For model uncertainty, we propose the first Laplace approximation of the weight posterior that scales to large neural networks with skip connections that have high-dimensional outputs. Empirically, we demonstrate that modelling spatial pixel correlation allows the Laplacian Segmentation Network to successfully assign high epistemic uncertainty to out-of-distribution objects appearing within images.

Bayesian Metric Learning for Uncertainty Quantification in Image Retrieval

We propose the first Bayesian encoder for metric learning. Rather than relying on neural amortization as done in prior works, we learn a distribution over the network weights with the Laplace Approximation. We actualize this by first proving that the contrastive loss is a valid log-posterior. We then propose three methods that ensure a positive definite Hessian. Lastly, we present a novel decomposition of the Generalized Gauss-Newton approximation. Empirically, we show that our Laplacian Metric Learner (LAM) estimates well-calibrated uncertainties, reliably detects out-of-distribution examples, and yields state-of-the-art predictive performance.

Laplacian Autoencoders for Learning Stochastic Representations

Established methods for unsupervised representation learning such as variational autoencoders produce none or poorly calibrated uncertainty estimates making it difficult to evaluate if learned representations are stable and reliable. In this work, we present a Bayesian autoencoder for unsupervised representation learning, which is trained using a novel variational lower-bound of the autoencoder evidence. This is maximized using Monte Carlo EM with a variational distribution that takes the shape of a Laplace approximation. We develop a new Hessian approximation that scales linearly with data size allowing us to model high-dimensional data. Empirically, we show that our Laplacian autoencoder estimates well-calibrated uncertainties in both latent and output space. We demonstrate that this results in improved performance across a multitude of downstream tasks.

Curious Explorer: a provable exploration strategy in Policy Learning

Having access to an exploring restart distribution (the so-called wide coverage assumption) is critical with policy gradient methods. This is due to the fact that, while the objective function is insensitive to updates in unlikely states, the agent may still need improvements in those states in order to reach a nearly optimal payoff. For this reason, wide coverage is used in some form when analyzing theoretical properties of practical policy gradient methods. However, this assumption can be unfeasible in certain environments, for instance when learning is online, or when restarts are possible only from a fixed initial state. In these cases, classical policy gradient algorithms can have very poor convergence properties and sample efficiency. In this paper, we develop Curious Explorer, a novel and simple iterative state space exploration strategy that can be used with any starting distribution $\rho$. Curious Explorer starts from $\rho$, then using intrinsic rewards assigned to the set of poorly visited states produces a sequence of policies, each one more exploratory than the previous one in an informed way, and finally outputs a restart model $\mu$ based on the state visitation distribution of the exploratory policies. Curious Explorer is provable, in the sense that we provide theoretical upper bounds on how often an optimal policy visits poorly visited states. These bounds can be used to prove PAC convergence and sample efficiency results when a PAC optimizer is plugged in Curious Explorer. This allows to achieve global convergence and sample efficiency results without any coverage assumption for REINFORCE, and potentially for any other policy gradient method ensuring PAC convergence with wide coverage. Finally, we plug (the output of) Curious Explorer into REINFORCE and TRPO, and show empirically that it can improve performance in MDPs with challenging exploration.