Affine Tracing: A New Paradigm for Probabilistic Linear Solvers

Probabilistic linear solvers (PLSs) return probability distributions that quantify uncertainty due to limited computation in the solution of linear systems. The literature has traditionally distinguished between Bayesian PLSs, which condition a prior on information obtained from projections of the linear system, and probabilistic iterative methods (PIMs), which lift classical iterative solvers to probability space. In this work we show this dichotomy to be false: Bayesian PLSs are a special case of non-stationary affine PIMs. In addition, we prove that any realistic affine PIM is calibrated. These results motivate a focus on (non-stationary) affine PIMs, but their practical adoption has been limited by the significant manual effort required to implement them. To address this, we introduce affine tracing, an algorithmic framework that automatically constructs a PIM from a standard implementation of an affine iterative method by passing symbolic tracers through the computation to build an affine computational graph. We show how this graph can be transformed to compute posterior covariances, and how equality saturation can be used to perform algebraic simplifications required for computation under specific prior choices. We demonstrate the framework by automatically generating a probabilistic multigrid solver and evaluate its performance in the context of Gaussian process approximation.

Constructive Disintegration and Conditional Modes

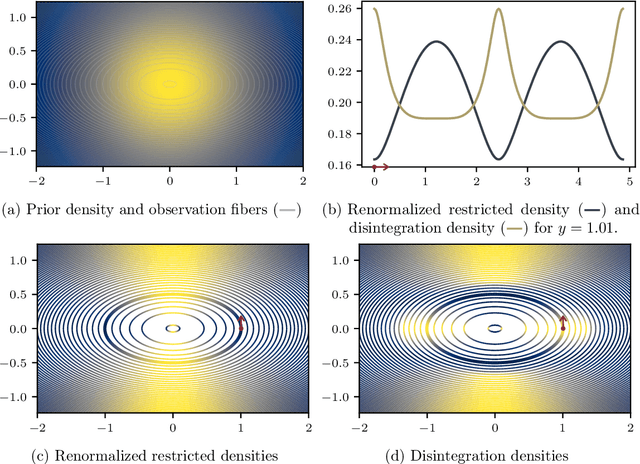
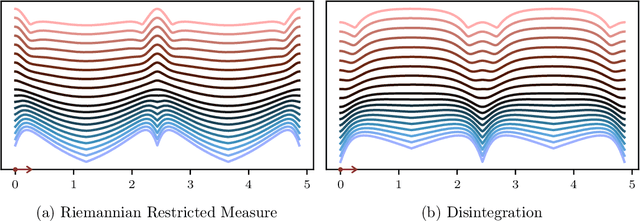
Conditioning, the central operation in Bayesian statistics, is formalised by the notion of disintegration of measures. However, due to the implicit nature of their definition, constructing disintegrations is often difficult. A folklore result in machine learning conflates the construction of a disintegration with the restriction of probability density functions onto the subset of events that are consistent with a given observation. We provide a comprehensive set of mathematical tools which can be used to construct disintegrations and apply these to find densities of disintegrations on differentiable manifolds. Using our results, we provide a disturbingly simple example in which the restricted density and the disintegration density drastically disagree. Motivated by applications in approximate Bayesian inference and Bayesian inverse problems, we further study the modes of disintegrations. We show that the recently introduced notion of a "conditional mode" does not coincide in general with the modes of the conditional measure obtained through disintegration, but rather the modes of the restricted measure. We also discuss the implications of the discrepancy between the two measures in practice, advocating for the utility of both approaches depending on the modelling context.

laplax -- Laplace Approximations with JAX

The Laplace approximation provides a scalable and efficient means of quantifying weight-space uncertainty in deep neural networks, enabling the application of Bayesian tools such as predictive uncertainty and model selection via Occam's razor. In this work, we introduce laplax, a new open-source Python package for performing Laplace approximations with jax. Designed with a modular and purely functional architecture and minimal external dependencies, laplax offers a flexible and researcher-friendly framework for rapid prototyping and experimentation. Its goal is to facilitate research on Bayesian neural networks, uncertainty quantification for deep learning, and the development of improved Laplace approximation techniques.

Flexible and Efficient Probabilistic PDE Solvers through Gaussian Markov Random Fields

Mechanistic knowledge about the physical world is virtually always expressed via partial differential equations (PDEs). Recently, there has been a surge of interest in probabilistic PDE solvers -- Bayesian statistical models mostly based on Gaussian process (GP) priors which seamlessly combine empirical measurements and mechanistic knowledge. As such, they quantify uncertainties arising from e.g. noisy or missing data, unknown PDE parameters or discretization error by design. Prior work has established connections to classical PDE solvers and provided solid theoretical guarantees. However, scaling such methods to large-scale problems remains a fundamental challenge primarily due to dense covariance matrices. Our approach addresses the scalability issues by leveraging the Markov property of many commonly used GP priors. It has been shown that such priors are solutions to stochastic PDEs (SPDEs) which when discretized allow for highly efficient GP regression through sparse linear algebra. In this work, we show how to leverage this prior class to make probabilistic PDE solvers practical, even for large-scale nonlinear PDEs, through greatly accelerated inference mechanisms. Additionally, our approach also allows for flexible and physically meaningful priors beyond what can be modeled with covariance functions. Experiments confirm substantial speedups and accelerated convergence of our physics-informed priors in nonlinear settings.

FSP-Laplace: Function-Space Priors for the Laplace Approximation in Bayesian Deep Learning

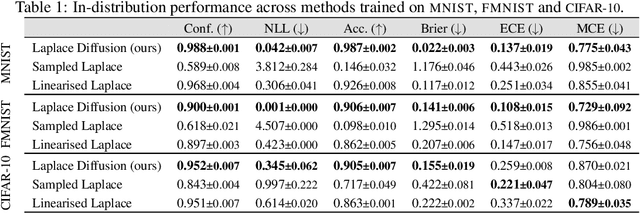
Laplace approximations are popular techniques for endowing deep networks with epistemic uncertainty estimates as they can be applied without altering the predictions of the neural network, and they scale to large models and datasets. While the choice of prior strongly affects the resulting posterior distribution, computational tractability and lack of interpretability of weight space typically limit the Laplace approximation to isotropic Gaussian priors, which are known to cause pathological behavior as depth increases. As a remedy, we directly place a prior on function space. More precisely, since Lebesgue densities do not exist on infinite-dimensional function spaces, we have to recast training as finding the so-called weak mode of the posterior measure under a Gaussian process (GP) prior restricted to the space of functions representable by the neural network. Through the GP prior, one can express structured and interpretable inductive biases, such as regularity or periodicity, directly in function space, while still exploiting the implicit inductive biases that allow deep networks to generalize. After model linearization, the training objective induces a negative log-posterior density to which we apply a Laplace approximation, leveraging highly scalable methods from matrix-free linear algebra. Our method provides improved results where prior knowledge is abundant, e.g., in many scientific inference tasks. At the same time, it stays competitive for black-box regression and classification tasks where neural networks typically excel.

Scaling up Probabilistic PDE Simulators with Structured Volumetric Information

Modeling real-world problems with partial differential equations (PDEs) is a prominent topic in scientific machine learning. Classic solvers for this task continue to play a central role, e.g. to generate training data for deep learning analogues. Any such numerical solution is subject to multiple sources of uncertainty, both from limited computational resources and limited data (including unknown parameters). Gaussian process analogues to classic PDE simulation methods have recently emerged as a framework to construct fully probabilistic estimates of all these types of uncertainty. So far, much of this work focused on theoretical foundations, and as such is not particularly data efficient or scalable. Here we propose a framework combining a discretization scheme based on the popular Finite Volume Method with complementary numerical linear algebra techniques. Practical experiments, including a spatiotemporal tsunami simulation, demonstrate substantially improved scaling behavior of this approach over previous collocation-based techniques.

Linearization Turns Neural Operators into Function-Valued Gaussian Processes

Modeling dynamical systems, e.g. in climate and engineering sciences, often necessitates solving partial differential equations. Neural operators are deep neural networks designed to learn nontrivial solution operators of such differential equations from data. As for all statistical models, the predictions of these models are imperfect and exhibit errors. Such errors are particularly difficult to spot in the complex nonlinear behaviour of dynamical systems. We introduce a new framework for approximate Bayesian uncertainty quantification in neural operators using function-valued Gaussian processes. Our approach can be interpreted as a probabilistic analogue of the concept of currying from functional programming and provides a practical yet theoretically sound way to apply the linearized Laplace approximation to neural operators. In a case study on Fourier neural operators, we show that, even for a discretized input, our method yields a Gaussian closure--a structured Gaussian process posterior capturing the uncertainty in the output function of the neural operator, which can be evaluated at an arbitrary set of points. The method adds minimal prediction overhead, can be applied post-hoc without retraining the neural operator, and scales to large models and datasets. We showcase the efficacy of our approach through applications to different types of partial differential equations.

Reparameterization invariance in approximate Bayesian inference

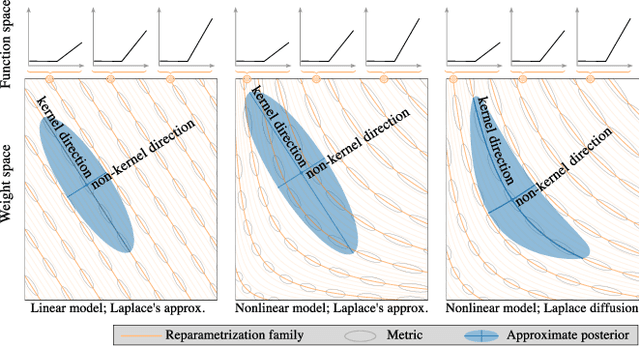
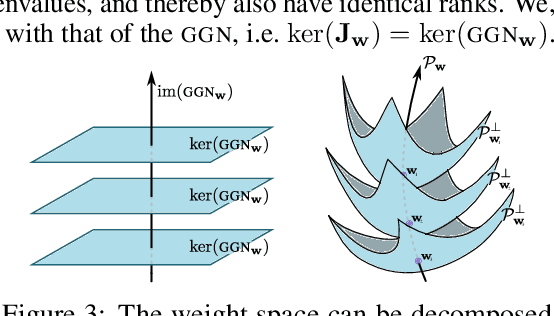
Current approximate posteriors in Bayesian neural networks (BNNs) exhibit a crucial limitation: they fail to maintain invariance under reparameterization, i.e. BNNs assign different posterior densities to different parametrizations of identical functions. This creates a fundamental flaw in the application of Bayesian principles as it breaks the correspondence between uncertainty over the parameters with uncertainty over the parametrized function. In this paper, we investigate this issue in the context of the increasingly popular linearized Laplace approximation. Specifically, it has been observed that linearized predictives alleviate the common underfitting problems of the Laplace approximation. We develop a new geometric view of reparametrizations from which we explain the success of linearization. Moreover, we demonstrate that these reparameterization invariance properties can be extended to the original neural network predictive using a Riemannian diffusion process giving a straightforward algorithm for approximate posterior sampling, which empirically improves posterior fit.

Computation-Aware Kalman Filtering and Smoothing

Kalman filtering and smoothing are the foundational mechanisms for efficient inference in Gauss-Markov models. However, their time and memory complexities scale prohibitively with the size of the state space. This is particularly problematic in spatiotemporal regression problems, where the state dimension scales with the number of spatial observations. Existing approximate frameworks leverage low-rank approximations of the covariance matrix. Since they do not model the error introduced by the computational approximation, their predictive uncertainty estimates can be overly optimistic. In this work, we propose a probabilistic numerical method for inference in high-dimensional Gauss-Markov models which mitigates these scaling issues. Our matrix-free iterative algorithm leverages GPU acceleration and crucially enables a tunable trade-off between computational cost and predictive uncertainty. Finally, we demonstrate the scalability of our method on a large-scale climate dataset.

Sample Path Regularity of Gaussian Processes from the Covariance Kernel

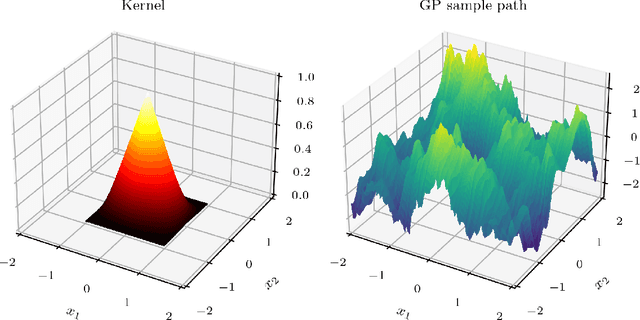
Gaussian processes (GPs) are the most common formalism for defining probability distributions over spaces of functions. While applications of GPs are myriad, a comprehensive understanding of GP sample paths, i.e. the function spaces over which they define a probability measure on, is lacking. In practice, GPs are not constructed through a probability measure, but instead through a mean function and a covariance kernel. In this paper we provide necessary and sufficient conditions on the covariance kernel for the sample paths of the corresponding GP to attain a given regularity. We use the framework of H\"older regularity as it grants us particularly straightforward conditions, which simplify further in the cases of stationary and isotropic GPs. We then demonstrate that our results allow for novel and unusually tight characterisations of the sample path regularities of the GPs commonly used in machine learning applications, such as the Mat\'ern GPs.