Asymmetric Duos: Sidekicks Improve Uncertainty

The go-to strategy to apply deep networks in settings where uncertainty informs decisions--ensembling multiple training runs with random initializations--is ill-suited for the extremely large-scale models and practical fine-tuning workflows of today. We introduce a new cost-effective strategy for improving the uncertainty quantification and downstream decisions of a large model (e.g. a fine-tuned ViT-B): coupling it with a less accurate but much smaller "sidekick" (e.g. a fine-tuned ResNet-34) with a fraction of the computational cost. We propose aggregating the predictions of this \emph{Asymmetric Duo} by simple learned weighted averaging. Surprisingly, despite their inherent asymmetry, the sidekick model almost never harms the performance of the larger model. In fact, across five image classification benchmarks and a variety of model architectures and training schemes (including soups), Asymmetric Duos significantly improve accuracy, uncertainty quantification, and selective classification metrics with only ${\sim}10-20\%$ more computation.

Computation-Aware Gaussian Processes: Model Selection And Linear-Time Inference

Model selection in Gaussian processes scales prohibitively with the size of the training dataset, both in time and memory. While many approximations exist, all incur inevitable approximation error. Recent work accounts for this error in the form of computational uncertainty, which enables -- at the cost of quadratic complexity -- an explicit tradeoff between computation and precision. Here we extend this development to model selection, which requires significant enhancements to the existing approach, including linear-time scaling in the size of the dataset. We propose a novel training loss for hyperparameter optimization and demonstrate empirically that the resulting method can outperform SGPR, CGGP and SVGP, state-of-the-art methods for GP model selection, on medium to large-scale datasets. Our experiments show that model selection for computation-aware GPs trained on 1.8 million data points can be done within a few hours on a single GPU. As a result of this work, Gaussian processes can be trained on large-scale datasets without significantly compromising their ability to quantify uncertainty -- a fundamental prerequisite for optimal decision-making.

Theoretical Limitations of Ensembles in the Age of Overparameterization

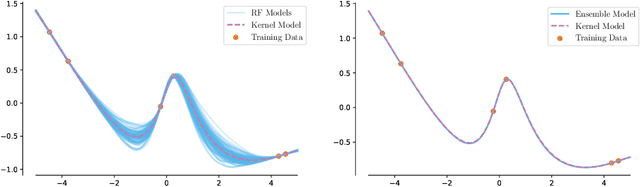
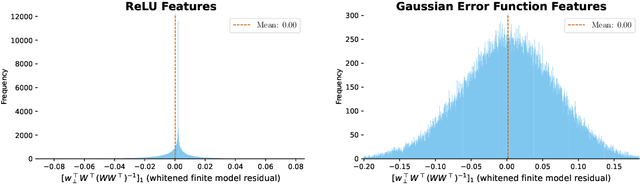
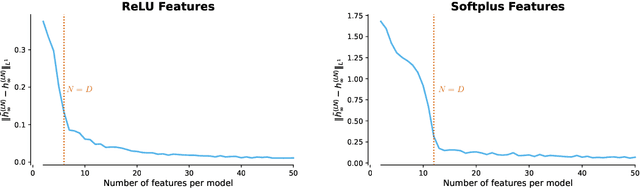
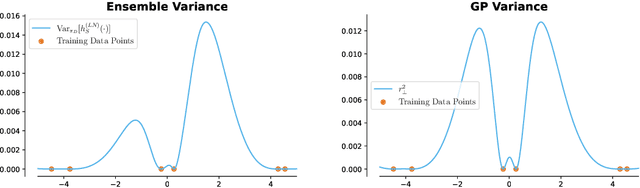
Classic tree-based ensembles generalize better than any single decision tree. In contrast, recent empirical studies find that modern ensembles of (overparameterized) neural networks may not provide any inherent generalization advantage over single but larger neural networks. This paper clarifies how modern overparameterized ensembles differ from their classic underparameterized counterparts, using ensembles of random feature (RF) regressors as a basis for developing theory. In contrast to the underparameterized regime, where ensembling typically induces regularization and increases generalization, we prove that infinite ensembles of overparameterized RF regressors become pointwise equivalent to (single) infinite-width RF regressors. This equivalence, which is exact for ridgeless models and approximate for small ridge penalties, implies that overparameterized ensembles and single large models exhibit nearly identical generalization. As a consequence, we can characterize the predictive variance amongst ensemble members, and demonstrate that it quantifies the expected effects of increasing capacity rather than capturing any conventional notion of uncertainty. Our results challenge common assumptions about the advantages of ensembles in overparameterized settings, prompting a reconsideration of how well intuitions from underparameterized ensembles transfer to deep ensembles and the overparameterized regime.

How Useful is Intermittent, Asynchronous Expert Feedback for Bayesian Optimization?

Bayesian optimization (BO) is an integral part of automated scientific discovery -- the so-called self-driving lab -- where human inputs are ideally minimal or at least non-blocking. However, scientists often have strong intuition, and thus human feedback is still useful. Nevertheless, prior works in enhancing BO with expert feedback, such as by incorporating it in an offline or online but blocking (arrives at each BO iteration) manner, are incompatible with the spirit of self-driving labs. In this work, we study whether a small amount of randomly arriving expert feedback that is being incorporated in a non-blocking manner can improve a BO campaign. To this end, we run an additional, independent computing thread on top of the BO loop to handle the feedback-gathering process. The gathered feedback is used to learn a Bayesian preference model that can readily be incorporated into the BO thread, to steer its exploration-exploitation process. Experiments on toy and chemistry datasets suggest that even just a few intermittent, asynchronous expert feedback can be useful for improving or constraining BO. This can especially be useful for its implication in improving self-driving labs, e.g. making them more data-efficient and less costly.

Online Continual Learning of Video Diffusion Models From a Single Video Stream

Diffusion models have shown exceptional capabilities in generating realistic videos. Yet, their training has been predominantly confined to offline environments where models can repeatedly train on i.i.d. data to convergence. This work explores the feasibility of training diffusion models from a semantically continuous video stream, where correlated video frames sequentially arrive one at a time. To investigate this, we introduce two novel continual video generative modeling benchmarks, Lifelong Bouncing Balls and Windows 95 Maze Screensaver, each containing over a million video frames generated from navigating stationary environments. Surprisingly, our experiments show that diffusion models can be effectively trained online using experience replay, achieving performance comparable to models trained with i.i.d. samples given the same number of gradient steps.

Approximation-Aware Bayesian Optimization

High-dimensional Bayesian optimization (BO) tasks such as molecular design often require 10,000 function evaluations before obtaining meaningful results. While methods like sparse variational Gaussian processes (SVGPs) reduce computational requirements in these settings, the underlying approximations result in suboptimal data acquisitions that slow the progress of optimization. In this paper we modify SVGPs to better align with the goals of BO: targeting informed data acquisition rather than global posterior fidelity. Using the framework of utility-calibrated variational inference, we unify GP approximation and data acquisition into a joint optimization problem, thereby ensuring optimal decisions under a limited computational budget. Our approach can be used with any decision-theoretic acquisition function and is compatible with trust region methods like TuRBO. We derive efficient joint objectives for the expected improvement and knowledge gradient acquisition functions in both the standard and batch BO settings. Our approach outperforms standard SVGPs on high-dimensional benchmark tasks in control and molecular design.

MCMC-driven learning

This paper is intended to appear as a chapter for the Handbook of Markov Chain Monte Carlo. The goal of this chapter is to unify various problems at the intersection of Markov chain Monte Carlo (MCMC) and machine learning$\unicode{x2014}$which includes black-box variational inference, adaptive MCMC, normalizing flow construction and transport-assisted MCMC, surrogate-likelihood MCMC, coreset construction for MCMC with big data, Markov chain gradient descent, Markovian score climbing, and more$\unicode{x2014}$within one common framework. By doing so, the theory and methods developed for each may be translated and generalized.

Layerwise Proximal Replay: A Proximal Point Method for Online Continual Learning

In online continual learning, a neural network incrementally learns from a non-i.i.d. data stream. Nearly all online continual learning methods employ experience replay to simultaneously prevent catastrophic forgetting and underfitting on past data. Our work demonstrates a limitation of this approach: networks trained with experience replay tend to have unstable optimization trajectories, impeding their overall accuracy. Surprisingly, these instabilities persist even when the replay buffer stores all previous training examples, suggesting that this issue is orthogonal to catastrophic forgetting. We minimize these instabilities through a simple modification of the optimization geometry. Our solution, Layerwise Proximal Replay (LPR), balances learning from new and replay data while only allowing for gradual changes in the hidden activation of past data. We demonstrate that LPR consistently improves replay-based online continual learning methods across multiple problem settings, regardless of the amount of available replay memory.

A Sober Look at LLMs for Material Discovery: Are They Actually Good for Bayesian Optimization Over Molecules?

Automation is one of the cornerstones of contemporary material discovery. Bayesian optimization (BO) is an essential part of such workflows, enabling scientists to leverage prior domain knowledge into efficient exploration of a large molecular space. While such prior knowledge can take many forms, there has been significant fanfare around the ancillary scientific knowledge encapsulated in large language models (LLMs). However, existing work thus far has only explored LLMs for heuristic materials searches. Indeed, recent work obtains the uncertainty estimate -- an integral part of BO -- from point-estimated, non-Bayesian LLMs. In this work, we study the question of whether LLMs are actually useful to accelerate principled Bayesian optimization in the molecular space. We take a sober, dispassionate stance in answering this question. This is done by carefully (i) viewing LLMs as fixed feature extractors for standard but principled BO surrogate models and by (ii) leveraging parameter-efficient finetuning methods and Bayesian neural networks to obtain the posterior of the LLM surrogate. Our extensive experiments with real-world chemistry problems show that LLMs can be useful for BO over molecules, but only if they have been pretrained or finetuned with domain-specific data.

Large-Scale Gaussian Processes via Alternating Projection

Gaussian process (GP) hyperparameter optimization requires repeatedly solving linear systems with $n \times n$ kernel matrices. To address the prohibitive $\mathcal{O}(n^3)$ time complexity, recent work has employed fast iterative numerical methods, like conjugate gradients (CG). However, as datasets increase in magnitude, the corresponding kernel matrices become increasingly ill-conditioned and still require $\mathcal{O}(n^2)$ space without partitioning. Thus, while CG increases the size of datasets GPs can be trained on, modern datasets reach scales beyond its applicability. In this work, we propose an iterative method which only accesses subblocks of the kernel matrix, effectively enabling \emph{mini-batching}. Our algorithm, based on alternating projection, has $\mathcal{O}(n)$ per-iteration time and space complexity, solving many of the practical challenges of scaling GPs to very large datasets. Theoretically, we prove our method enjoys linear convergence and empirically we demonstrate its robustness to ill-conditioning. On large-scale benchmark datasets up to four million datapoints our approach accelerates training by a factor of 2$\times$ to 27$\times$ compared to CG.